Кулонов закон

| Електромагнетизам |
|---|
 |
У физици, Кулонов закон дефинише интензитет, правац и смер електростатичке силе којом непокретно наелектрисање малих димензија делује на друго. Та сила се често назива и Кулонова сила. Названа је по француском физичару Шарлу Кулону који је користио торзиону вагу како би је измерио. Закон гласи:
Интензитет електростатичке силе између два тачкаста наелектрисања је директно пропорционалан производу количина њихових наелектрисања, а обрнуто пропорционалан квадрату растојања између та два наелектрисања.
Историја
[уреди | уреди извор]Древне културе широм Медитерана су знале да поједини објекти, као што су шипке од ћилибара, при трљању са мачјим крзном могу да привуку лаке предмете попут перја. Талес из Милета је 600 година пре нове ере вршио огледе везане за статички електрицитет. Из проучавања је закључио да неки материјали, као минерал магнетита, сами показују магнетне особине, док је неке материјале да би показали магнетне особине потребно претходно утрљати, те да се тако ћилибар намагнетисава утрљавањем, тј. трењем. Талес је погрешио верујући да се привлачност догађа због магнетног дејства, јер ће касније наука доказати везу између магнетизма и електрицитета.

Струја ће остати нешто више од интелектуалне радозналости миленијумима, све до 1600. године, када је енглески научник Вилијам Гилберт успео пажљивим проучавањем електрицитета и магнетизма, да направи разлику између магнетизма и статичког електрицитета произведеног трљањем ћилибаром. Он је измислио нову латинску реч lectricus (у директном преводу од ћилибара или попут ћилибара, из грчке речи за ћилибар ηλεκτρον [електрон]). Та реч се односила на особину привлачења малих објеката након трења. То је асоцирало Томаса Брауна да у својој књизи „Pseudodoxia Epidemica“ 1646. године по први пут у историји користи енглеске речи електрични и струја.
Поједини научници са почетка 18. века су сумњали да електрична сила, попут гравитационе, се смањује са дистанцом (тј., да је обрнуто сразмерна квадрату растојања) укључујући Данијела Бернулија и Алесандра Волта. Обојица су мерила силу између плоче кондензатора, а Франц Епинус који је објавио инверзно-квадратни закон у 1758. години.
На основу експеримената на наелектрисаним сферама, Џозеф Пристли у Енглеској био је међу првима који предлаже да електрична снага прати инверзно-квадратни закон, сличан Њутновом закону универзалне гравитације. Међутим, он није генерализовао или разрадио ово. У 1767. години, он је претпоставио да сила између два пуњења варира као обрнутом квадрату растојања.

У 1769, шкотски физичар Џон Робисон је најавио да, према његовим мерењима, сила одбијања између две сфере са истим знаком варира као x -2.06.
Почетком 1770-их година, зависност силе између наелектрисаних тела на обе дистанце и пуњења већ је било откривено, али није објављено, по Хенрију Кевендишу из Енглеске.
Коначно, 1785те године, француски физичар Шарл-Огистен де Кулон је објавио своја прва три извештаја о електрицитету и магнетизму, где је изнео свој закон. Ова публикација је од суштинског значаја за развој теорије електромагнетизма. Он је користио торзиону вагу за проучавање одбојне и привлачне силе наелектрисаних честица, и утврдио да је величина електричне силе између две кључне тачке пуњења директно пропорционална производу пуњења и обрнуто пропорционална квадрату растојања између њих.
Торзиона вага састоји се од шипке закачена кроз своју средину танким влакнима. Влакна делује као јако слаба торзиона опруга. У Кулоновом експерименту, торзиона вага је изолациони штап са лоптом са металном кошуљицом на једног краја закачена свиленим концем. Лопта је била наелектрисана са познатим наелектрисањем за статички електрицитет, а друга наелектрисана лопта истог поларитета је доведен до ње. Две наелектрисане кугле су се одбиле једна од друге, уврћући влакна под одређеним углом, који се може очитати са скале на инструменту.
Знајући колика је сила потребна да се уврну влакана до датог угла, Кулон је успео да израчуна силе између кугли и изведе свој инверзно-квадрати пропорционални закон.
Закон
[уреди | уреди извор]Кулонов закон наводи да:
- Интензитет електростатичке силе између два тачкаста наелектрисања је директно пропорционалан производу количина њихових наелектрисања, а обрнуто пропорционалан квадрату растојања између та два наелектрисања.

Кулонов закон се може навести као једноставан математички израз. Скаларни и векторски облици математичке једначине су
| и | , |
где је ke Кулонова константа, q1 i q2 су магнитуде наелектрисања, скаларно r је растојање између наелектрисања, вектор је векторско растојање између наелектрисања и (Јединични вектор од q2 do q1). Векторски облик једначине изнад израчунава силу примењује на q1 од стране q2. Ако је r12 уместо тога искоришћен, онда се ефекат на q2 може наћи. Такође се може израчунати коришћењем Њутновог трећег закона : .
Јединице
[уреди | уреди извор]Електромагнетна теорија обично се изражава помоћу Међународног система јединица. Сила се мери у њутнима, наелектрисање у кулонима, и удаљеност у метрима. Кулонова константа је дата са . Константа је диелектрична константа слободног простора у C2 m−2 N−1. И је релативна диелектрична константа материјала у који је уроњено наелектрисање, па је бездимензиона. У Међународном систему изведених јединица за електрично поље је волт по метру, Њутн по Кулону, или тесла метара у секунди. Кулонов закон и Кулонова константа може се тумачити у различитим условима:
- атомска јединица. У атомским јединицама снага се изражава у Хартрееју по Бохраовом радијусу, наелектрисање у смислу основног наелектрисања, и даљина у смислу Бохровог радијуса.
- електростатичке јединице или Гаусове јединице. У електростатичке јединице и Гаусова јединица, јединица пуњење се дефинише на такав начин да Кулонова константа k нестаје јер има вредност једног и постаје бездимензиона .
Електрично поље
[уреди | уреди извор]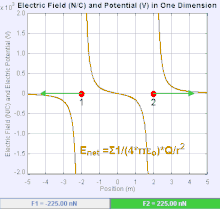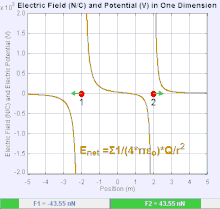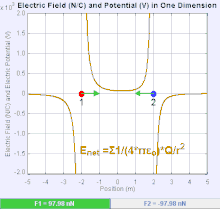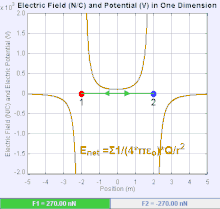
Електрично поље је векторско поље које повезује сваку тачку у простору Кулонових сила кроз који пролази тест наелектрисања. У најједноставнијем случају, сматра се да ће бити генерисан од стране искључиво једног извора наелектрисане тачке. Снага и правац силе Кулона на тест наелектрисања зависи од електричног поља да се нађе у њему, тако да је . Ако се поље генерише позитивно наелектрисаном изворном тачком , смер електричног поља тачака дуж линија усмерених радијално ка споља од њега, односно у смеру позитивном набоју тачка теста померило би се ако је стављено на поље. За негативно наелектрисани извор наелектрисања, правац је радијално ка унутра.
Величина електричног поља се може извести из Кулоновог закона. Избором једне од тачака наелектрисања да је извор, а други да буде тест пуњења, прати да је из Кулоновог закона величина овог електричног поља направљен од стране једног извора наелектрисане тачка на одређеној удаљености од њега у вакууму даје:
- .
Кулонова константа
[уреди | уреди извор]Кулонов константа пропорционалности је фактор који се појављује у Кулоновом закону, као и у другим електро-сродних формула. Означава , позната као константна електричне силе или електростатичка константа, па индексни .
Тачна вредност Кулонове константе је:
Стање пуноважности
[уреди | уреди извор]Постоје два услова које треба испунити за важења Кулоновог закона:
- Разматрана наелектрисање морају бити део тачке наелектрисања.
- Они треба да буду стационарне у међусобном односу једна на другу.
Скаларни облик
[уреди | уреди извор]
Када је то само од интереса да се зна величина електростатичке силе (а не његов смер), је лакше да се размотри скаларни облик закона. Скаларни облик Кулоновог закона се односи на обим и знак електростатичке силе која делује истовремено на две тачке оптужнице и на следећи начин:
где је растојање и Кулонова константа. Ако је производ позитиван, сила између два наелектрисања је одбојна, а ако је производ негативан, сила између њих је привлачна.
Векторски облик
[уреди | уреди извор]
Кулонов закон каже да се електростатичка сила на које утиче наелектрисање, на позицији , у близини другог наелектрисања, на позицији , у вакууму је једнака:
Где је , јединични вектор , и електрични константа .
Векторски облик Кулоновог закона је једноставна скаларна дефиниција закона са датим правцем од векторске јединице, , паралелно са линијом од наелектрисања до наелектрисања . Ако оба наелектрисања имају исти знак онда је производ позитиван и правац силе на је дат од стране ; Наелектрисања одбијају једни друге. Ако наелектрисања имају супротне знаке онда производа је негативан и правац силе је дат од стране ;Наелектрисања привлаче једни друге.
Електростатичка сила на које утиче наелектрисање , према трећем Њутновом закону, је .
Систем изолованих наелектрисања
[уреди | уреди извор]Закон поклапања Кулоновом закону дозвољава да буде проширен на било који број тачака наелектрисања. Сила која делује на тачку наелектрисања, због тога сто је система тачака наелектрисања једноставно векторско додавање појединачних сила које делују само на тачку наелектрисања због сваког наелектрисања. Резултат је вектор сила паралелна са електричним пољем вектора у том тренутку, с уклоњеном тачком наелектрисања.
Сила на малом наелектрисању , на позицији , због система изоловано наелектрисање у вакууму је:
Где су и величина и положај, у односно на наелектрисања, је јединични вектор у правцу (Вектор показује на основно наелектрисање од до )).
Непрекидна расподела наелектрисања
[уреди | уреди извор]У овом случају, принцип линеарне суперпозиције се такође користи. За непрекидну расподелу наелектрисања, интеграл целом региону који садржи наелектрисање одговара бесконачном збиру, третирајући сваки инфинитезимални елемент простора као тачка наелектрисања . Расподела наелектрисања је обично линеарна, површинска или запреминска.
За линеарну расподелу наелектрисања (добра апроксимација за наелектрисање у жице), где даје наелектрисање по јединици дужине на позицији , и је инфинитезимални елемент дужине,
- .
За расподелу површинског наелектрисања, где даје наелектрисање по јединици површине, на позицији и је инфинитезимални елемент простора,
За расподелу запреминског наелектрисања (као што су наелектрисање у оквиру расутих метала), где даје наелектрисање по јединици запремине, на позицији , и је инфинитезимални елемент запремине,
Сила на мали тест наелектрисања на позицији у вакууму дат од стране интеграла преко расподеле наелектрисања:
Једноставан експеримент за проверу Кулоновог закона
[уреди | уреди извор]Могуће проверити Кулонов закон са једноставним експериментом. Размотримо две мале сфере масе и истим знаком наелектрисања , које виси о два ужета занемарљиве масе дужине . Три силе које делују на сваку сфери су: тежина , затегнутост конопца и електричне силе .
У стању равнотеже:
|
|
(1) |
и:
|
|
(2) |
Дељењем (1) са (2):
|
|
(3) |
Ако је растојање између наелектрисаних сферама, онда је одбојна сила између њих , под претпоставком да је Кулонов закон тачно, је једнака
|
|
(Кулонов закон) |
тако да је:
|
|
(4) |
Ако сада разелектришемо једну од сфера, а ставимо је у контакту са наелектрисаном сфером, сваки од њих добија наелектрисање q/2. У стању равнотеже, растојање између наелектрисања ће бити и одбојност сила између њих ће бити:
|
|
(5) |
Знамо да је . И:
Дељењем (3) са (4), добијамо:
|
|
(6) |
Мерењем углове и и растојање између наелектрисања и могуће је проверити да једнакост важи, узимајући у обзир експерименталну грешку. У пракси, углови могу бити тешко измериви, па ако је дужина ужета довољно велика, углови ће бити довољно мали да би се добила следећа апроксимација:
|
|
(7) |
Користећи ову апроксимацију, однос (6) постаје много једноставнији израз:
|
|
(8) |
На овај начин, верификација је ограничена на мерење растојања између наелектрисања и провера да ли је подела апроксимира теоријску вредност.
Електростатичке апроксимације
[уреди | уреди извор]У обема формулацијама, скаларној и векторској, Кулонов закон је тачан само ако су наелектрисања у мировању, а остаје приближно тачан за мање брзине кретања. Када се наелектрисања крећу, ствара се магнетско поље које мења Кулонове силе које делују на наелектрисања. Сила која настаје услед магнетског поља може се сматрати као сила електростатичког поља под условом да се у обзир узме и Ајнштајнова теорија релативитета.
Види још
[уреди | уреди извор]Литература
[уреди | уреди извор]- Coulomb, Charles Augustin (1788) [1785]. „Premier mémoire sur l’électricité et le magnétisme”. Histoire de l’Académie Royale des Sciences. Imprimerie Royale. стр. 569—577.
- Coulomb, Charles Augustin (1788) [1785]. „Second mémoire sur l’électricité et le magnétisme”. Histoire de l’Académie Royale des Sciences. Imprimerie Royale. стр. 578—611.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd изд.). Prentice Hall. ISBN 978-0-13-805326-0.
- Tipler, Paul A.; Mosca, Gene (2008). Physics for Scientists and Engineers (6th изд.). New York: W. H. Freeman and Company. ISBN 978-0-7167-8964-2. LCCN 2007010418.
- Young, Hugh D.; Freedman, Roger A. (2010). Sears and Zemansky's University Physics : With Modern Physics (13th изд.). Addison-Wesley (Pearson). ISBN 978-0-321-69686-1.
Спољашње везе
[уреди | уреди извор]- MISN-0-114 Кулонов закон од J. Ковач за Project PHYSNET.
- Coulomb's Law on Project PHYSNET
- Electricity and the Atom Архивирано на сајту Wayback Machine (21. фебруар 2009)—a chapter from an online textbook
- A maze game for teaching Coulomb's Law—a game created by the Molecular Workbench software
- Electric Charges, Polarization, Electric Force, Coulomb's Law Walter Lewin, 8.02 Electricity and Magnetism, Spring 2002: Lecture 1 (video). MIT OpenCourseWare. License: Creative Commons Attribution-Noncommercial-Share Alike.











































































![{\displaystyle {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Longrightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c9166e7d5f120fd7a63a5c035838dbe36df9dcf)