Пенроузово поплочавање
Пенроузово поплочавање је апериодичко (понавља се, али не увек на исти начин) поплочавање равни плочицама у облику ромба које је 1973. открио Роџер Пенроуз.
Два првобитно откривена пара облика који учествују у поплочавању су „змај“ и „стрела“. Сваки од ових парова се може поделити на два једнакокрака троугла (Робинсонове троуглове) који се користе за конструкцију. Робинсонови троуглови су једнакокраки троуглови са угловима 36,36 и 108 или 72,72 и 36. Сваки од ових троуглова има странице чији је однос дужина (1+√5):2. Овај однос је познат као златни пресек.
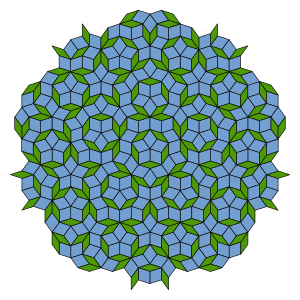
Плочице се не могу транслирати, одосно не постоји део поплочавања који се може више пута понављати у току поплочавања; међутим случајеви попут овог на слици имају осну и петоструку реотацијску симетрију. Ово пополочавање је и дводимензионални квазикристал (круто тело чија је кристална решетка непериодична).
Независно од Пенроуза овакав начин поплочавања је открио и Роберт Амен, у приближно истом временском периоду.
Ден Шектмен је 1982. године објавио да је узорак руде алуминијумовог мангана створио оштри дифрактограм с петоструком симетријом. Де Брујин показује да се Пенроузово поплочавање може добити пројекцијом из петодимензионалне коцкасте решетке. Пенроузово поплочавање је временом постало један од најчувенијих и најизучаванијих квазикристала.
