Алгоритми претраживања

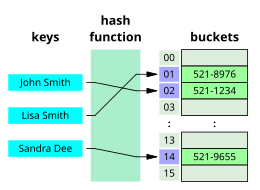
У рачунарству и информатици алгоритам претраживања је процес којим се у скупу података проналази жељени податак на основу одређене идентификације.

Класификација

Подела се може извршити на основу погодности одређеног алгоритма за претрагу над статичким, односно динамичким, скупом података, и сложености његове имплементације:

Основни алгоритми претраживања
Стабла претраживања
Хеширање

Основни алгоритми претраживања

Ови алгоритми су најједноставнији за имплементацију, а погодни су за претрагу статичких скупова података (уређених и неуређених табела). Овој групи спадају:

Секвенцијално претраживање
Бинарно претраживање

Секвенцијално претраживање

Овај начин претраге је најједноставнији за имплементацију, али има најлошије перформансе. Састоји се у томе да се крене редом и проверава за сваки елемент да ли је тај елемент онај који тражимо. Уколико јесте, претрага се успешно завршава, у супротном се иде даље, све док се не нађе жељени елемент или се не испитају сви елементи.

Претпоставимо да желимо да пронађемо позицију неког одређеног елемента у низу целих бројева. Пример овог алгоритма у програмском језику C, изгледао би овако:

int sek_pret(int niz[], int n, int k) {
    int i=0;
    while(i<n) {
      if(k==niz[i]) {
         return i;
      } else {
         i++;
      }
    }
    return -1;
}

У претходном примеру, niz[] је низ који претражујемо, n је број елемената у низу, k је жељени елемент, а i је тренутна итерација кроз низ.

Могу се извршити побољшања претходног алгоритма, заснована на претпоставци временске локалности. Сматра се, да ће тражени кључ, у блиској будућности, поново бити потребан, па се он помера ка почетку низа, како би раније био пронађен. Методом транспозиције, кључ се пребацује за једно место унапред, док се код методе пребацивања на почетак пронађени елемент ставља на почетак низа.

Бинарно претраживање

Овај алгоритам применљив је само на уређене скупове података. Не провера се редом да ли је тренутни елемент тај који тражимо, већ се почиње од елемента који је у средини уређеног низа.

Претпоставимо да је низ (табела) уређен растуће. Уколико је елемент у средини мањи од оног који тражимо, претрагу ћемо наставити у горњој половини низа, у супротном, ако је елемент у средини већи од оног који тражимо, претрагу настављамо у доњој половини низа. Затим поново узимамо средњи елемент преосталог интервала за претрагу и поредимо са жељеним елементом. Претрага се наставља док се елемент не пронађе, а у случају да елемент није пронађен у тој итерацији, интервал се дели на пола. Ако се интервал састоји само од једног елемента, а то није жељени елемент, претрага се завршава неуспешно, тј. тражени елемент није пронађен у датом низу.

Претпоставимо да желимо да пронађемо позицију неког одређеног елемента у уређеном низу целих бројева. Пример овог алгоритма у програмском језику C, изгледао би овако:

int bin_pret(int niz[], int n, int k) {
    int donja_gran= 0;
    int gornja_gran= n - 1;
    while(donja_gran<=gornja_gran) {
      int sred = (donja_gran+gornja_gran)/2;
      if(k==niz[sred]) {
         return sred;
      } else {
           if(k<niz[sred]) {
              gornja_gran = sred - 1;
           } else {
              donja_gran = sred + 1;
           }
      }
    }
    return -1;
}

Стабла претраживања

Код ове групе алгоритама, имплементација је нешто сложенија, али се они могу применити, једнако добро, и на скупове статичких и на скупове динамичких података. Операције над структурама података, који омогућавају успешност ових алгоритама, су захтевније у погледу меморије, процесорског и програмерског времена.

Стабло бинарног претраживања
Стабло м-арног претраживања
B стабло
B+ стабло
B* стабло
Стабла дигиталног претраживања

Стабло бинарног претраживања

Стабло бинарног претраживања примењује се на скуповима података који се динамички мењају, јер се његова структура ефикасно модификује приликом убацивања/брисања елемената.

Оно се дефинише као бинарно стабло за које важи:

за сваки кључ K постоји највише један чвор l где је kljuc(l) = K
кључеви свих потомака у левом стаблу су мањи од кључа тог чвора
кључеви свих потомака у десном стаблу су већи од кључа тог чвора

Претрага на одређени кључ у бинарном стаблу претраге, у програмском језику C изгледала би овако:

int bin_stab_pret(Cvor *koren, int k) {
    Cvor pom = koren;
    while((pom!=null) && (k!=pom->kljuc)) {
      if(k < pom->kljuc) {
         pom = pom->levi_potomak;
      } else {
         pom = pom->desni_potomak;
      }
    }
    return pom;
}

Функцији предајемо корен стабла који је типа „Чвор“ и жељени кључ. Чвор је структура која у себи садржи показивач на десног и левог потомка, као и кључ који чвор садржи. Функција враћа показивач на чвор који је резултат претраге (null pointer у случају неуспешне претраге).

Стабло м-арног претраживања

Стабло м-арног претраживања је стабло које задовољава следеће особине:

чвор стабла се састоји од показивача на подстабла и, највише м, кључева, који су организовани тако да сваки кључ раздваја два показивача(подстабла)
кључеви унутар једног чвора су растуће уређени
у произвољном чвору, сви кључеви подстабла, на који показује показивач лево од кључа К, су мањи од кључа К
у произвољном чвору, сви кључеви подстабла, на који показује показивач десно од кључа К, су већи од кључа К
подстабла, на која указују показивачи из вишег слоја стабла м-арног претраживања, су такође стабла м-арног претраживања

Претрага у овом стаблу се врши тако што се кључ прво тражи у кореном чвору. Ако се ту не нађе, онда се тражи одговарајући показивач на неко подстабло у којем је можда жељени кључ. Тај показивач се налази тако што се у кореном чвору нађу два узастопна кључа К_i-1 и К_i-2 таква да је жељени кључ већи од К_i-1, а мањи од К_i-2. Показивач између та два кључа указује на онај чвор у којем настављамо претрагу. Процес је претраге у било ком чвору је исти као у кореном, и он се понаваља све док се не нађе кључ или док не дођемо до неког од листова стабла у којем такође нисмо пронашли тражени кључ, а потрага се не може наставити јер нема више подстабала у којима можемо да вршимо претрагу.

Претрага на нивоу чвора се може извршити секвенцијалним или бинарним начином претраживања.

Литература

D. E. Knuth (1998). The Art of Computer Programming Volume 3: Sorting and Searching (3rd изд.). Addison-Wesley Professional. ISBN 978-0-201-48541-7.
William H. Press; Brian P. Flannery; Saul A. Teukolsky; William T. Vetterling (1992). Numerical Recipes in C: The Art of Scientific Computing (Second изд.). Cambridge University Press. ISBN 978-0-521-43108-8.
Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Stein, Clifford (2009). Introduction to Algorithms (Third изд.). The MIT Press. ISBN 978-0-262-03384-8.