Batervortov filter


Batervortov filter je tip filtra koji ima ravnu opadajuču karakteristiku, u propusnom opsegu i smatra se kompromisom između Čebiševog i Beselovog filtra. Filter je nazvan po Britanskom inžinjeru Stivenu Batervortu (Stephen Butterworth) koji ga je prvi opisao 1930. godine.
Uopšteno
[уреди | уреди извор]Ovaj termin se više odnosi na tip odziva nego na specifičan tip filtra. Prenosna funkcija se tako dimenzioniše da nema „talasanja“ u propusnom opsegu i opada prema nuli u nepropusnom[1]. Ovo se postiže izjednačavanjem izvoda prenosne funkcije sa nulom, na centralnoj učestanosti filtra (to je npr. nula za niskopropusne filtre).
Ovdje ću detaljnije obraditi niskopropusne, visokopropusne kao i filtre propusnike opsega, u slučaju kad je dato kolo nižeg ili kolo višeg reda. Filtri prvog reda su oni kod kojih odziv opada 6dB po oktavi (20dB po dekadi). Kod filtera drugog reda, riječ je o -12 dB/oct, dok se kod trećeg reda radi o -18/oct.
Dizajn filtra
[уреди | уреди извор]Postoje nekoliko različitih topologija, odnosno vrsta izrade ovog linearnog, analognog filtra. Najkorištenije su Kauerova i Salen-Ki topologije.
Salen-Ki topologija
[уреди | уреди извор]Salen-Ki topologija koristi aktivne i pasivne komponente (uglavnom su to operacioni pojačavači, otpornici i kondenzatori). Svaki stepen Salen-Kija dodaje po par polova. Na kraju se svi stepeni filtra povežu redno.[2]
Analiza generičkog primjera
[уреди | уреди извор]Sa slike se vidi da je kod OP-a zatvorena negativna sprega pa je stoga V-=V+=Vout. Napišimo jednačinu za čvor X:
ili:
Struja je ista kroz elemente Z2 i Z4 pa je očigledno:
Iz čega dobijamo
Uvrstimo li to u jednačinu za čvor X, dobijamo:
Iz čega dobijamo prenosnu funkciju:
Ako bi komponenta Z3 bila uzemljena, filter bi bio djelitelj napona (na Z1 i Z3), kaskadno vezan sa djeliteljem napona na Z2 i Z3.
Zavisno od odabira pasivnih komponenti za (otpornika i kondenzatora) može se dobiti niskopropusni, visokopropusni ili filter propusnik opsega.
Primjer analize niskopropusnog filtra
[уреди | уреди извор]Za amortizaciju (kao bafer) se koristi OP, ali se takođe može koristiti i BJT emiter . Komponente su odabrane na sljedeći način: Z1=R1; Z2=R2; Z3=1/(sC1); Z4=1/(sC2) .
Uvrštavanjem ovih vrijednosti u izraz za prenosnu funkciju koji smo dobili u prethodnom slučaju, dobijamo:
Da bi zadovoljili opštu formulu:
svodimo na:
iz čega se lako zaključi da je:
- tj. : Takođe se dobija da je :
predstavlja cutoff frekvenciju ( naravno cutoff kružnu učestanost), dok je faktor dobrote (bezdimenziona veličina) koji opisuje koliko je visok i širok pik odziva filtra. Veći Q faktor označava manji gubitak energije u odnosu na frekvenciju, tj. oscilacije se sporije gase (odumiru).
Dizajner mora odabrati parametre i zavisno od situacije. Naprimjer, Batervortov filter drugog reda, koji ima najveći flet odziv u propusnom opsegu, ima koji iznosi . Imamo 2 parametra za podešavanje, a 4 nepoznate (), obično se uzima jedan otpornik kao odnos sa drugim (tipa ). Isto se uradi i kod odabira kondendzatora.
Primjer odabira elemenata
[уреди | уреди извор]
Kolo sa slike ima od 15.9 kHz i faktor od 0.5. Prenosna funkcija izgleda ovako:
Poslije uvrštavanja (; ), dobijamo:
Odavde vidimo da se jednostavnom promjenom odnosa R,C ili m,n može postići ista frekvencija i faktor dobrote za bilo koji filter.
Primjer analize visokopropusnog filtra
[уреди | уреди извор]
Analiziraćemo visokopropusni filter drugog reda, sa slike. Njegova prenosna funkcija će biti oblika:
Iz jednačina:
Sređivanjem se dobija:
Upoređivanjem jednačina se dobija:
Primjer analize filtra propusnika opsega
[уреди | уреди извор]
Na slici je prikazan bandpass filter implementiran u VCVS topologiji. Iako nije ista topologija, metod analize je sličan i lakše ga je objasniti na ovom primjeru. Prenosna funkcija ovog filtra je data izrazom:
Centralna učestanost (frekvencija gdje odziv ima svoj pik) se dobija izrazom:
Naponski djeljitelj u kolu sa negativnom povratnom spregom kontroliše gejn. "Unutrašnji gejn" od operacionog pojačavača je
dok je gejn pojačavača, na frekvenciji pika, dat izrazom:
Vidimo da se mora držati ispod 3 da filter ne bi oscilirao. Filter se obično optimizuje odabirom i .
Butterworth filtri višeg reda
[уреди | уреди извор]Red filtra je broj njegovih polova i koji ćemo upotrijebiti, zavisi od praktične potrebe. Aktivan filter sa N polova ima rolloff rate od N x 6dB/oktavi (N x 20dB/dekadi). Slično, odziv visokopropusnog filtra sa N polova povecava se po N x 6dB/oktavi, sve do cutoff frekvencije. U oba slučaja, f_c je definisano kao:
Magnituda naponske prenosne funkcije za niskopropusne filtre N-tog reda je:

Za visokopropusne filtre N-tog reda, magnituda naponske prenosne funkcije je:
Na slici je prikazan niskopropusni Batervortov filter trećeg reda (ima 3 pola). Tri otpornika su jednaka a odnos između kapacitivnosti tako što se prvi i drugi izvod prenosne funkcije izjednače sa nulom.
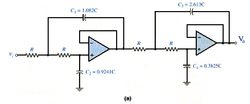
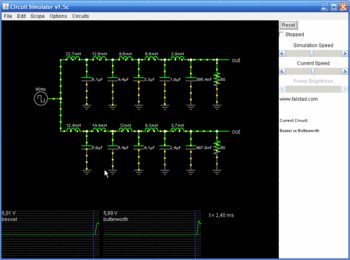
Filtri višeg reda se mogu konstruisati dodavanjem još RC mreža. Međutim, efekat punjenja za svaku dodatnu RC mrežu postaje sve vidljiviji. Ovo se prevazilazi tako što se kaskadno (redno) vežu filtri drugog reda sa OP-om (znači svaki filter ima po jedan OP u sebi).Zbog niske izlazne otpornosti OP-a, gotovo da nema efekta punjenja između kaskada. Primjer takvog filtra se može vidjeti na slici. Maksimalno ravan odziv se ne dobija prostim vezivanjem na red ovih dvo-polnih filtera. Potrebno je uskladiti kapacitivnosti izjednačavanjem prva tri izvoda funkcije prenosa, sa nulom. Na sličan način se mogu konstruisati i filtri višeg reda. Propusnici i nepropusnici opsega koriste sličnu konfiguraciju.
Primjer rješavanja niskopropusnog aktivnog Butterworth filtra trećeg reda
[уреди | уреди извор]Od raznih topologija koje su nam na raspolaganju za izradu filtra višeg reda, Sallen-Key zahtijeva najmanji broj komponenti pa je takav filter lakše analizirati (npr. samo jedan OP za 3-polni odziv 18 dB/oct). Slijedi opis analize sklopa sa slike 6.
Posmatramo čvor 3b (gdje je v3 = v3a = v3b). Jednačina za napon čvora se može napisati i ovako:
Označimo: Zatim:
Naponi za ostale čvorove glase:
Prenosna funkcija H(s) = Vout/Vin, sada izgleda H(s)=
Primijetimo da je opšti oblik za H(s) 3-polnog Butterworth niskopropusnog filtra na cutoff frekvenciji od 1 rad/sec:
Primijetimo:
gdje je Kac = M.
Izaberemo izlazni rast od: Kac = 3 (9,5 dB)
Takođe, izaberemo sljedeće vrijednosti komponenti:
Rješavajuči po R1, R2, R3 i R4 dobijamo:
- R1= 816.46 Om, R2= 481.26 Om, R3= 848.33 Om, R4= 10 kOm
Dozvoljeno nam je da promijenimo vrijednosti R1-R4 prema EIA standardu od 1% tolerancije po dekadi:
- R1= 825 Om, R2= 487 Om, R3= 845 Om, R4= 20 kOm
Praktični savjeti:
- Za različite vrijednosti rasta mogu se koristiti vrijednosti komponenti sa tabele ispod, ili svaki blok zasebno rješavati za različitu vrijednost Kac. Koristite samo pozitivne pozitivne potkorjene vrijednosti. Programski paket Mathcad(TM) može pomoći pri računu.
| M(Kac) | 0dB | 6dB | 12dB | 18dB | 24dB | 30dB | 36dB |
|---|---|---|---|---|---|---|---|
| R1(Ω) | 1.292 | 15.652 | 1.624 | 4.305 | 3.246 | 1.437 | 3.234 |
| R2(Ω) | 2.093 | 14.694 | 4.067 | 1.750 | 2.134 | 16.260 | 7.198 |
| R3(Ω) | 3.698 | 4.348 | 15.144 | 13.276 | 1.444 | 42.794 | 42.950 |
| R4(Ω) | 0 | 10.000 | 30.000 | 70.000 | 15.000 | 31.000 | 63.000 |
| R5(Ω) | ∞ | 10.000 | 10.000 | 10.000 | 1.000 | 1.000 | 1.000 |
| C1(F) | 10-3 | 10-4 | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 |
| C2(F) | 10-3 | 10-4 | 10-4 | 10-4 | 10-4 | 10-5 | 10-5 |
| C3(F) | 10-4 | 10-4 | 10-4 | 10-4 | 10-3 | 10-4 | 10-4 |
| M(Kac) | 42dB | 48dB | 54dB | 60dB | 66dB | 72dB | 78dB |
|---|---|---|---|---|---|---|---|
| R1(Ω) | 1.640 | 1.242 | 2.243 | 1.030 | 1.137 | 1.700 | 6.053 |
| R2(Ω) | 13.615 | 69.066 | 32.123 | 185.004 | 285.242 | 136.553 | 47.723 |
| R3(Ω) | 4.479 | 116.556 | 138.815 | 5.249 | 308.473 | 430.832 | 346.170 |
| R4(Ω) | 127.000 | 25.500 | 51.100 | 102.300 | 20.470 | 40.950 | 81.910 |
| R5(Ω) | 1.000 | 100 | 100 | 100 | 10 | 10 | 10 |
| C1(F) | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 | 10-3 |
| C2(F) | 10-5 | 10-6 | 10-6 | 10-6 | 10-7 | 10-7 | 10-7 |
| C3(F) | 10-3 | 10-4 | 10-4 | 10-3 | 10-4 | 10-4 | 10-4 |
Primjer tropolnog Batervortovog filtra
[уреди | уреди извор]
U prikazanoj šemi:
- 1. Tranzistori Mm6, 7, 8, 9 i 10 su tranzistori za strujno ogledalo u šemi za mješač.
- 2. Prvi transkonduktor čine Mf1 i 2 (i aktivno opterećenje). On se ponaša kao zaštita između mješača i filtra.
- 3. Rf1 i Cf1 su dva od uređaja koji se koriste u normalizovanom niskopropusnom filtru (podešenom na frekvenciju i impedansu)
- 4. Četiri transkonduktorske ćelije (Mf2-10 i odgovarajuća aktivna opterećenja) i kondenzator Cf2 čine aktivni induktor.
- 5. Rf2 i Cf3 su krajnje komponente normalizovanog niskopropusnog filtra.
Mreža za pomjeranje faze ima centralnu frekvenciju od 5,5 MHz i propusni opseg (gdje je fazni pomak linearan) od oko 1 MHz. To je u suštini paralelna RLC mreža gdje je induktor aktivni induktor.

U gornjoj šemi:
- 1. Kondenzatori Cps1 i 2 su izabrani tako da je njihova reaktansa jednaka reaktansi Rps1.
- 2. R je izabrano tako da određeni faktor dobrote Q (i potom širinu propusnog opsega fazno pomjerajuće mreže).
- 3. Cps3 i aktivni induktor (dvije transkonduktorske ćelije) podešavaju centralnu frekvenciju u mreži za pomjeranje faze.
Kauer topologija
[уреди | уреди извор]
Kauer topologija koristi pasivne komponente (kondenzatore i kalemove) za implementaciju linearnog analognog filtra. Izraz za k-ti element je dat u formi:
- ; k = neparno
- ; k = parno
Filter se može realizovati i sa serijski vezanim induktivitetom na početku, ali se u tom slučaju uzima da je Lk od k neparno a Ck od k parno.
Reference
[уреди | уреди извор]- ^ Giovanni Bianchi and Roberto Sorrentino (2007). Electronic filter simulation & design. McGraw-Hill Professional. стр. 17–20. ISBN 9780071494670.
- ^ Donald A Neamen (2009). Microelectronics Circuit Analysis and Design. McGraw-Hill. стр. 1050-1070. ISBN 978-0-07-338064-3, 9780073380643.
Литература
[уреди | уреди извор]- Donald A Neamen (2009). Microelectronics Circuit Analysis and Design. McGraw-Hill. стр. 1050-1070. ISBN 978-0-07-338064-3, 9780073380643.
- Giovanni Bianchi and Roberto Sorrentino (2007). Electronic filter simulation & design. McGraw-Hill Professional. стр. 17–20. ISBN 9780071494670.

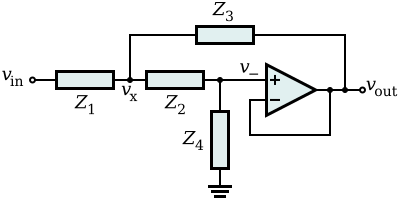


















































![{\displaystyle {\frac {\frac {M}{R_{1}\cdot R_{2}\cdot R_{3}\cdot C_{1}\cdot C_{2}\cdot C_{3}}}{\left[s^{3}+\left({\frac {1}{R_{1}\cdot C_{1}}}+{\frac {1}{R_{2}\cdot C_{1}}}+{\frac {1}{R_{2}\cdot C_{2}}}+{\frac {1-M}{R_{3}\cdot C_{3}}}+{\frac {1}{R_{3}\cdot C_{2}}}\right)\cdot s^{2}+\left({\frac {R_{3}\cdot C_{3}+R_{1}\cdot C_{3}+R_{2}\cdot C_{3}+C_{1}\cdot R_{1}+\left(1-M\right)\cdot \left(R_{1}+R_{2}\right)\cdot C_{2}}{R_{1}\cdot R_{2}\cdot R_{3}\cdot C_{1}\cdot C_{2}\cdot C_{3}}}\right)\cdot s+{\frac {1}{R_{1}\cdot R_{2}\cdot R_{3}\cdot C_{1}\cdot C_{2}\cdot C_{3}}}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e8ee843fec7366eeb49552f53d163f3b10cfc6d)







