Пређи на садржај

Директан ациклични граф

С Википедије, слободне енциклопедије
(преусмерено са Directed acyclic graph)
Пример директног ацикличног графа

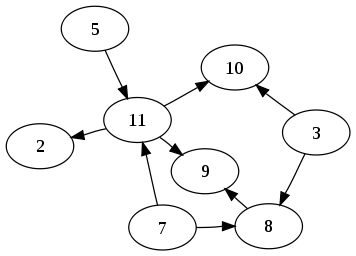
Директан ациклични граф (ДАГ) у математици и информатици је директан граф без усмерених циклуса. Састоји се од збира чворова и усмерених грана, свака грана повезује један чвор са другим, тако да не постоји начин да се почне у неком чвору в и прати редослед грана који се на крају петље опет враћа на чвор в.[1][2][3]

ДАГ може да се користи за моделирање многих различитих врста информација. Достизање везе у ДАГ форми делимичног реда, и било ког коначно делимичног реда може бити представљен од стране ДАГ који користи достизање. Колекција задатака која се мора одредити у низу, уз ограничење да морају бити извршени одређени задаци раније од других, може бити представљен као ДАГ са чвором за сваки задатак и граном за сваку препреку; алгоритми за тополошко уређење могу се користити за одређивање исправног низа. Додатно, ДАГ може да се користи као простор ефикасне заступљености низова са преклапајућим поднизовима. ДАГ се такође користи за представљање система догађаја или потенцијалних догађаја и узрочно–последичних односа између њих. ДАГ се такође може користити за моделовање процеса у којима је проток података у доследном правцу кроз мрежу процесора, или стања репозиторијума у верзији контроле система.

Одговарајући концепт неусмерених графова је шума, један неусмерен граф без циклуса. Избор оријентације за шуме производи посебну врсту директног ацикличног графа који се зове оријентисано стабло. Међутим, постоје многе друге врсте директног ацикличног графа које нису формиране прем оријентацији грана једног неусмереног ацикличног графа. Осим тога, сваки неусмерени граф има ацикличну оријентацију, доделу правца за своје гране које га чине директним ацикличним графом. Из тих разлога било би прецизније назвати директан ациклични граф ацикличан усмерени граф или ацикличан диграф.

Математичка својства

[уреди | уреди извор]

Достизање, транзитивно затворење, и транзитивна редукција

[уреди | уреди извор]
Хасеов дијаграм који представља парцијалан ред ⊆ између подскупова од три елемента скупа.

Сваки усмерени ациклични граф доводи до парцијалног реда ≤ на својим чворовима, где је у ≤ в тачно када постоји директан пут од у до в у ДАГ.[4] Међутим, много различитих ДАГ може довести до тог истог достижности односа:[5] на пример, ДАГ са две гране а → б и б → ц има исто достизање као и граф са три гране а → б, б → ц, и а → ц. Ако је Г ДАГ, његова транзитивна редукција је граф са најмањим бројем грана који представља исто достизање као и за Г, а његово транзитивно затворење је граф са највише грана који представља исто достизање. Транзитивна редукција и транзитивно затворење су јединствено дефинисани за ДАГ; насупрот томе, за усмерени граф који није ацикличан, не може бити више од једног минималног подграфа са истим достизањем односа.[6]

Транзитивно затварање на Г има једну грану у → в за сваки везани пар у ≤ в различитих елемената у достизању односа Г, и тако се може посматрати као директан превод достизања односа ≤ у граф - теоријском смислу: сваки парцијални ред скупа може се превести у ДАГ на овај начин. Ако ДАГ Г представља парцијални ред ≤, онда је транзитивна редукција од Г подграф од Г са једном граном у → в за сваки пар у пропратном односу ≤; транзитивне редукције су корисне у визуализацији парцијалних редова које они представљају, јер имају мање грана од других графова који представљају исте редове и самим тим доводе до једноставнијих цртежа графова. Хасе дијаграм парцијалног ред је цртеж транзитивне редукције у којима је оријентација сваке гране приказана тако да је почетни чвор гране на нижем нивоу него његов крајњи чвор.[7]

Тополошко сортирање

[уреди | уреди извор]

Сваки директан ациклични граф има тополошко сортирање, тј. редослед чворова је такав да се почетак крајње тачке сваке гране јавља раније у сортирању од краја крајње тачке гране. У принципу, ово сортирање није јединствено; ДАГ има јединствено тополошко сортирање ако и само ако има усмерен пут који садржи све врхове, у ком случају сортирање је исто као и ред у којем се чворови појављују на путу.[8] Породица тополошког сортирања једног ДАГ је иста као и породица линеарних продужетака достижности у односу на ДАГ,[9], тако било која два графа представљају исти парцијални ред са истим скупом тополошких редова.

Комбинаторно набрајање

[уреди | уреди извор]

Проблем графа набрајања бројања директног ацикличног графа испитивао је Робинсон (1973).[10] Број ДАГ са н обележених чворова, за н = 0, 1, 2, 3,....,(дозвољавајући да се ови бројеви појаве у било ком реду у тополошком сортирању ДАГ) је

1, 1, 3, 25, 543, 29281, 3781503, … (ред A003024 у OEIS).

Ови бројеви се могу израчунати понављањем везе:

[10]

Ерик В. Веинстејн је претпоставио,[11] а McKay et al. 2004 доказао,[12] да исти бројеви броје (0,1) матрице у којој су све својствене вредности позитивни реални бројеви. Доказ је бијекција: Матрица А је матрица повезаности ДАГ ако и само ако је А + И (0,1) матрица са свим својствено позитивним вредностима, где И означава матрицу идентитета. Зато што ДАГ не може имати циклус, његова суседна матрица мора имати нула дијагоналу, додајући И да сачува особине да су све матрице коефицијента 0 или 1.

Веза породице графа

[уреди | уреди извор]

Оријентисано стабло је усмерени граф формиран према оријентацији грана слободног стабла.[13] Свако оријентисано стабло је ДАГ. Конкретно, истина је да су стабла формирана на основу усмерења свих грана од споља ка корену стабла. Снажно недвосмислен граф представља усмерени граф у којем постоји највише једна усмерена путања (у оба смера) између било која два чвора; евентуално, то је ДАГ у којем, за сваки чвор в, постоји скуп чворова доступних из в обликовног стабла.[14]

Рачунарски проблеми

[уреди | уреди извор]

Тополошко сортирање и препознавање

[уреди | уреди извор]
Главни чланак: Тополошко сортирање

Тополошко сортирање је алгоритам проблема проналажења тополошког сортирања; може се решити у линеарном времену.[15] Канов алгоритам за тополошко сортирање гради чворове директног сортирања, одржавајући листу чворова који немају гране, повезујући их са чворовима који нису већ наведени, а више пута додајући један такав чвор на крај листе која се оснива.[16] Алтернативно, тополошко сортирање се може конструисати уназад после сортирања нумерације од прве претраге у дубину графа.[15]

Такође је могуће да се провери да ли је дати усмерени граф ДАГ у линеарном времену или је било покушаја да нађе тополошко сортирање а затим тестирање за сваку грану да ли је различито сортирање исправно[17] или алтернативно, за неке алгоритме тополошког сортирања, проверава се да ли алгоритам успешно сортира све чворове без грешке.[16]

Грађа цикличних графова

[уреди | уреди извор]

Сваки неусмерени граф може бити у ДАГ избором укупног сортирања својих чворова и оријентације својих грана из раније крајње тачке у сортиране касније крајње тачке. Међутим, различита потпуна сортирања могу довести до исте ацикличне оријентације. Број ацикличних оријентација је једнак |χ(−1)|, где је χ хроматски полином датог графа.[18]

Било који усмерени граф се може представити као ДАГ тако што се уклони скуп повратних чворова или скупа повратних лукова. Међутим, најмањи такав скуп је НП-тешки проблеми.[19] Произвољно усмерен граф може да се трансформише у ДАГ, назива се кондензација, уговарањем сваке од његових чврсто повезаних компоненти у један суперчвор.[20] Када је граф већ ацикличан његов најмањи скуп повратних информација чворова и скуп повратних информација лукова су празни, а његова кондензација је сам граф.

Транзитивно затворење и транзитивна редукција

[уреди | уреди извор]

Транзитивно затворење датог ДАГ, са n чворова и m грана, може се конструисати у времену O(mn) користећи или претрагу у ширину или претрагу у дубину ради тестирања достизања до сваког чвора. [21] Алтернативно, може се решити и у времену O(nω) где је ω < 2.373 експонент за брзо множење алгоритама матрице; ово је теоретски напредак у односу на O(mn) везан за густе графове. [22]

У свим овим алгоритмима транзитивног затворења, могуће је разликовати парове чворова који су доступни најмање једне путање дужине два или више од парова који се могу повезати само од дужине једне путање. Транзитивна редукција састоји се од грана чије су дужине једне путање једине путање које повезују своје крајње тачке. Стога, транзитивна редукција се може конструисати у истом асимптотском времену граничних линија као и транзитивна затвореност.[23]

Проблем затворења

[уреди | уреди извор]
Главни чланак: Проблем затворења

Проблем затворења узима као улаз директан ациклични граф са тежинама њених чворова и тражи минималну (или максималну) тежину затварања, скуп чворова без икаквих одлазећих грана. (Проблем може бити формулисан за усмерене графове без претпоставке да су ациклични, али без веће уопштености јер у овом случају је еквивалентан са проблемом кондензације графова.) Може се решити у полиномијалном времену користећи смањен максималан проблем тока.[24]

Апликације

[уреди | уреди извор]

Алгоритам путање

[уреди | уреди извор]

Неки алгоритми постају једноставнији када се користи ДАГ уместо општих графова, на основу принципа тополошког сортирања. На пример, могуће је наћи најкраће путеве и најдуже путеве са датим почетним чвором у ДАГ у линеарном времену обрадом чворова у тополошком реду, и израчунавање дужине пута за сваки чвор да буде минимална или максимална дужина добијена преко претходних грана. [25] Насупрот томе, за произвољне графове најкраћи пут може захтевати спорији алгоритам као што је Дајкстрин алгоритам или Белман-Фордов алгоритам,[26] и најдужи пут у произвољном графу је НП-тешки проблеми.[27]

Распоређивање

[уреди | уреди извор]

ДАГ репрезентације парцијалног сортирања има много захтева у распореду проблема за системе задатака са ограниченим сортирањем. [28] На пример, ДАГ може користити табелу за описивање зависности између ћелија: ако се једна ћелија израчунава по формули која укључује вредност друге ћелије, нацртати ДАГ грану од друге ћелије до прве. Ако се улазне вредности табеле промене, све преостале вредности табеле могу се прерачунати са једном променом по ћелији, од тополошког сортирања ћелија и поново вреднује сваку ћелију у том циљу.[29] Слични проблеми задатка сортирања настаје у прављењу фајлова за компилацију програма,[29] упутство за распоред за низак ниво оптимизације рачунарског програма,[30] и Перт распоред за управљање великих људских пројеката.[31] График зависности без кружне зависности облика директног ацикличног графа.

Обрада података мреже

[уреди | уреди извор]

Усмерен граф може да се користи за представљање мреже за обраду елемената; у овој формулацији подаци, улазни подаци обрађују елемент преко претходних грана и напуштају елемент преко одлазећих грана. Примери овога обухватају следеће:

  • У дизајну електронских кола, статички комбинациони логички блокови могу бити представљени као ациклични системи логичких кола који израчунава функцију једног улаза, где су улаз и излаз функције представљени као појединачни бит. У принципу, излаз ових блокова не може да се користи као улаз осим ако је заузет од стране регистра или главног елемента који одржава своја ациклична својства.[32] Шема електронског кружног пута или на папиру или у бази података је облик директног ацикличног графа који користи објекте или компоненте за формирање усмерене референце на нижем нивоу компоненте. Сама електронска кола нису нужно ациклична или усмерена.
  • Проток података програмски језици описују системе вредности који се односе на међусобно директан ациклични граф. Када промене једну вредност, његови наследници се прерачунавају; свака вредност је процењена као функција својих претходника у ДАГ.[33]
  • У компајлеру, равна линија кода (који је, секвенца исказа без петље или условна грана) може бити представљен ДАГ који описује улазе и излазе сваке аритметичке операције која се обавља у коду; ово представљање омогућава да компајлер обавља заједничко елиминисање подизраз ефикасно.[34]
  • У већини система за табеле, графикон зависности повезује једну ћелију са другом уколико прва ћелија чува формулу која користи вредност друге ћелије тако да мора бити директан ациклични граф. Циклуси зависности су поништени јер они узрокују ћелије укључене у циклус који нема добро дефинисану вредност. Поред тога, захтева се да зависност буде ациклична и омогућава тополошко сортирање које се користи да закаже поновни прерачун вредности ћелија када се мења табела.[29]

Узрочне структуре

[уреди | уреди извор]

Графови који имају чворове који представљају догађаје, и гране које представљају узрочно-везе између догађаја, често су ациклични[35] - уређење чворова у линеарном распореду времена, све стрелице указују у истом правцу као време, од родитеља на дете (због узрочности утиче будућност а не прошлост), и на тај начин немају петље.

На пример, Бајесова мрежа представља систем вероватноће догађаја као чворова у директном ацикличном графу, у којој се вероватоћа неког догађаја може израчунати из вероватноће својих претходника у ДАГ.[36] У том контексту, морални граф ДАГ је неусмерени граф створен додавањем (неусмерених) грана између свих родитеља истог чвора (понекад зовемо брак), а затим замените све усмерене гране са неусмереним гранама.[37]

Други тип графа са сличном узрочном структуром има утицај дијаграма, чворови на којима су представљене одлуке да буду или непознате информације, као и гране које представљају узрочне утицаје из једног чвора на други.[38] У епидемиологији, на пример, ови дијаграми се често користе за процену очекиване вреднсоти различитих избора за интервенцију.[39][40] Улога ДАГ у овим апликацијама је да га претвори иу узрочне-последичне претпоставке у условно независна ограничења, што се може прочитати из ДАГ користећи Пеарл д-сепарацију.[41] и тестиран у подацима.

Генеалогија и историјска верзија

[уреди | уреди извор]

Породица стабала се такође може посматрати као директан ациклични граф, са чвором за сваког члана породице и гране за сваку везу родитељ-дете.[42] Упркос имену, ти графови нису нужно стабла због могућности бракова између рођака (тако да дете има заједничког претка на обе стране мајке и оца) изазивајући педигре колапса. (Графови по мајчиној линији порекла ("мајка" односи између жена) и по очевој линији порекла ("отац" односи између мушкараца) су стабла у оквиру овог графа.) Зато што нико не може постати самостално предак, ови графови су циклични.

Из истог разлога, историјска верзија дистрибуираног управљачког система ревизије углавном има структуру директног ацикличног графа, у којима постоји чвор за сваку ревизију и гране повезују парове ревизије које су директно изведене од другог; ово нису стабла у целини због стапања.[43]

У многим случајним алгоритмима у рачунарској геометрији, алгоритам одржава историју ДАГ представља историјску верзију геометријске структуре током периода низа промена у структури. На пример, у случајном појединачном алгоритму за Делунаи триангулација, триангулација промене заменом једног троугла са три мања троугла када свака тачка дода, и "флип" операција замењује парове троуглова. Историја ДАГ за овај алгоритам има чворове за сваки троугао изграђен као део алгоритма, и гране сваког троугла, два или три троугла који га замењују. Тражење пута кроз овај ДАГ представља низ троуглова који садрже појединачну тачку која омогућава тачку локације пута која ће бити ефикасно одговорио.[44]

Сажимање података

[уреди | уреди извор]

Друга врста примене директног ацикличног графа настаје у сажетом представљању низа секвенци као путања у графу. На пример, усмерени ациклички граф речи је структура података у компјутерској науци формиран од стране директног ацикличног графа са једним извором и са гранама означеним словима или симболима; путеви од извора до понора у овом графу представљају скуп ниски, као што су Енглеске речи.[45] Било који низ секвенци се може представити као пут у стаблу, формирањем чвора стабла за сваки префикс секвенци и изграђивањем родитеља једног од тих чворова који представљају секвенцу са једним мање елементом; стабло формирано на овај начин са низом ниски зове се трие. Усмерен ациклични граф речи штеди простор над трие дозвољавајући да се путеви разилазе и поново придружују, тако да се скуп речи са истим могућим наставцима могу бити представљени једним чвором стабла.

Иста идеја користећи ДАГ представља породицу путања јавља се у бинарном дијаграму одлуке,[46][47] ДАГ - заснован на структури и подацима за представљање бинарних функција. У бинарном дијаграму одлуке, сваки не-потонули чвор обележен именом бинарне променљиве, а сваки потонули и свака грана је обележена 0 или 1. Функција вредности за било који истинити задатак променљиве је вредност у потонулом тражењу следећег пута, почевши од једног извора чвора, да на сваком не-потонулом чвору прати одлазну грану означену са вредношћу чвора променљиве. Баш као што се усмерени ациклични граф речи може посматрати као компликовани облик покушаја, бинарна одлука дијаграма се може посматрати као компликован облик стабла одлучивања која штеди простор тако што путање дозвољавају да се поново договоре о резултатима свих преосталих одлука.

Референце

[уреди | уреди извор]
  1. ^ Christofides, Nicos . Graph theory: an algorithmic approach. . Academic Press. 1975. pp. 170–174. 
  2. ^ Thulasiraman, K.; Swamy, M. N. S. . "5.7 Acyclic Directed Graphs", Graphs: Theory and Algorithms, John Wiley and Son. 1992. ISBN 978-0-471-51356-8. стр. 118.
  3. ^ Bang-Jensen, Jørgen. "2.1 Acyclic Digraphs", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag. 2008. ISBN 978-1-84800-997-4. стр. 32–34.
  4. ^ Kozen, Dexter . The Design and Analysis of Algorithms, Monographs in Computer Science. . Springer. 1992. ISBN 978-0-387-97687-7. 
  5. ^ Banerjee, Utpal . "Exercise 2(c)", Loop Transformations for Restructuring Compilers: The Foundations. . Springer. 1993. pp. 19. ISBN 978-0-7923-9318-4. 
  6. ^ Bang-Jensen, Jørgen; Gutin, Gregory Z. . "2.3 Transitive Digraphs, Transitive Closures and Reductions", Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics. . Springer. 2008. pp. 36–39. ISBN 978-1-84800-998-1. 
  7. ^ Jungnickel, Dieter . Graphs, Networks and Algorithms, Algorithms and Computation in Mathematics 5. . Springer. 2012. pp. 92–93. ISBN 978-3-642-32278-5. 
  8. ^ Sedgewick, Robert; Wayne, Kevin , "4,2,25 Unique topological ordering", Algorithms (4th ed.). . Addison-Wesley. 2011. pp. 598–599. ISBN 978-0-13-276256-4. 
  9. ^ Bender, Edward A.; Williamson, S. Gill , "Example 26 (Linear extensions – topological sorts)", A Short Course in Discrete Mathematics, Dover Books on Computer Science. . Courier Dover Publications. 2005. pp. 142. ISBN 978-0-486-43946-4. 
  10. ^ а б Robinson, R. W. (1973), „Counting labeled acyclic digraphs”, Ур.: Harary, F., New Directions in the Theory of Graphs, Academic Press, стр. 239—273 . See also Harary, Frank; Palmer, Edgar M. (1973), Graphical Enumeration, Academic Press, стр. 19, ISBN 978-0-12-324245-7 
  11. ^ Weisstein, Eric W., "Weisstein's Conjecture", MathWorld.
  12. ^ McKay, B. D.; Royle, G. F.; Wanless, I. M.; Oggier, F. E.; Sloane, N. J. A.; Wilf, H. (2004), "Acyclic digraphs and eigenvalues of (0,1)-matrices", Journal of Integer Sequences 7, Article 04.3.3.
  13. ^ Rebane, George; Pearl, Judea (1987), "The recovery of causal poly-trees from statistical data", in Proc. 3rd Annual Conference on Uncertainty in Artificial Intelligence (UAI 1987), Seattle, WA, USA, July 1987 (PDF). стр. 222–228.
  14. ^ Furnas, George W.; Zacks, Jeff (1994). „Multitrees: enriching and reusing hierarchical structure”. Proceedings of the SIGCHI conference on Human factors in computing systems celebrating interdependence - CHI '94. стр. 330—336. ISBN 0897916506. S2CID 18710118. doi:10.1145/191666.191778. 
  15. ^ а б Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. Introduction to Algorithms (2nd изд.). MIT Press and McGraw-Hill. ISBN 0-262-03293-7.  Section 22.4, Topological sort. стр. 549–552.
  16. ^ а б Jungnickel 2012, стр. 50–51
  17. ^ For depth-first search based topological sorting algorithm, this validity check can be interleaved with the topological sorting algorithm itself; see e.g. Skiena, Steven S. , The Algorithm Design Manual. . Springer. 2009. pp. 179–181. ISBN 978-1-84800-070-4. 
  18. ^ Stanley, Richard P. (1973). „Acyclic orientations of graphs”. Discrete Mathematics. 5 (2): 171—178. doi:10.1016/0012-365X(73)90108-8. 
  19. ^ Garey, Michael R.; Johnson, David S. , Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman. 1979. ISBN 978-0-7167-1045-5. Problems GT7 and GT8. стр. 191–192.
  20. ^ Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, John Wiley & Sons. стр. 63.
  21. ^ Skiena 2009, стр. 495.
  22. ^ Skiena 2009, стр. 496.
  23. ^ Bang-Jensen & Gutin (2008). стр. 38.
  24. ^ Picard, Jean-Claude (1976). „Maximal Closure of a Graph and Applications to Combinatorial Problems”. Management Science. 22 (11): 1268—1272. doi:10.1287/mnsc.22.11.1268. 
  25. ^ Cormen 2001, стр. 592–595.
  26. ^ Cormen et al. 2001, Sections 24.1, The Bellman–Ford algorithm. стр. 588–592, and 24.3, Dijkstra's algorithm. стр. 595–601.
  27. ^ Cormen 2001, стр. 966.
  28. ^ Skiena 2009, стр. 469.
  29. ^ а б в Gross, Yellen & Zhang 2013, стр. 1181
  30. ^ Srikant, Y. N.; Shankar, Priti . The Compiler Design Handbook: Optimizations and Machine Code Generation, (2nd ed.). . CRC Press. 2007. pp. 19–39. ISBN 978-1-4200-4383-9. 
  31. ^ Wang, John X. . What Every Engineer Should Know About Decision Making Under Uncertainty. . CRC Press. 2002. pp. 160. ISBN 978-0-8247-4373-4. 
  32. ^ Sapatnekar, Sachin , Timing. . Springer. 2004. pp. 133. ISBN 978-1-4020-7671-8. 
  33. ^ Programming Symposium. Lecture Notes in Computer Science. 19. 1974. ISBN 978-3-540-06859-4. S2CID 38955165. doi:10.1007/3-540-06859-7. 
  34. ^ Touati & de Dinechin 2014, стр. 123
  35. ^ Gopnik, Alison; Schulz, Laura . Causal Learning. . Oxford University Press. 2007. pp. 4. ISBN 978-0-19-803928-0. 
  36. ^ Shmulevich, Ilya; Dougherty, Edward R. , Probabilistic Boolean Networks: The Modeling and Control of Gene Regulatory Networks, Society for Industrial and Applied Mathematics. 2010. ISBN 978-0-89871-692-4. стр. 58.
  37. ^ Cowell, Robert G.; Dawid, A. Philip; Lauritzen, Steffen L.; Spiegelhalter, David J. , "3.2.1 Moralization", Probabilistic Networks and Expert Systems. . Springer. 1999. pp. 31–33. ISBN 978-0-387-98767-5. 
  38. ^ Dorf, Richard C. . The Technology Management Handbook. . CRC Press. 1998. pp. 9–7. ISBN 978-0-8493-8577-3. 
  39. ^ Boslaugh, Sarah , Encyclopedia of Epidemiology, Volume 1, SAGE. 2008. ISBN 978-1-4129-2816-8. стр. 255.
  40. ^ Pearl, Judea (1995). „Causal diagrams for empirical research”. Biometrika. 82 (4): 669—688. doi:10.1093/biomet/82.4.669. 
  41. ^ Bayesian network
  42. ^ Kirkpatrick, B. B. (2011). „Haplotypes versus genotypes on pedigrees”. Algorithms for Molecular Biology : Amb. 6 (1): 10. PMC 3102622 Слободан приступ. PMID 21504603. doi:10.1186/1748-7188-6-10. 
  43. ^ Bartlang, Udo , Architecture and Methods for Flexible Content Management in Peer-to-Peer Systems. . Springer. 2010. pp. 59. ISBN 978-3-8348-9645-2. 
  44. ^ Pach, János; Sharir, Micha, Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical surveys and monographs 152, American Mathematical Society. ISBN 978-0-8218-7533-9. стр. 93–94.
  45. ^ Combinatorial Pattern Matching. Lecture Notes in Computer Science. 1264. 1997. стр. 116—129. ISBN 978-3-540-63220-7. S2CID 29560680. doi:10.1007/3-540-63220-4. 
  46. ^ Lee, C. Y. (1959). „Representation of Switching Circuits by Binary-Decision Programs”. Bell System Technical Journal. 38 (4): 985—999. doi:10.1002/j.1538-7305.1959.tb01585.x. 
  47. ^ Akers (1978). „Binary Decision Diagrams”. IEEE Transactions on Computers (6): 509—516. S2CID 21028055. doi:10.1109/TC.1978.1675141. 

Литература

[уреди | уреди извор]

Спољашње везе

[уреди | уреди извор]
Директан ациклични граф на Викимедијиној остави.
Преузето из „https://sr.wikipedia.org/w/index.php?title=Директан_ациклични_граф&oldid=28510317”