Poziciona notacija
Poziciona notacija, ili notacija u kojoj pozicija oređuje vrednost, metod je predstavljanja ili kodiranja brojeva. Poziciona notacija se razlikuje od drugih notacija (kao što su rimski brojevi) po njenoj upotrebi istog simbola za različite redove veličine (na primer, mesto jedinica, mesto desetica, mesto stotina). Time se znatno pojednostavljuje aritmetika, što je dovelo do brzog širenja notacije širom sveta.
Sa upotrebom radiks tačke (decimalne tačke kod osnove-10), notacija se može proširiti tako da obuhvata razlomke i numeričke ekspanzije realnih brojeva.
Vavilonski numerički sistem, čija je osnova 60, je bio prvi pozicioni sistem, i njegov uticaj je prisutan danas u načinu na koji se vreme i uglovi izražavaju u grupama od 60, poput 60 minuta u satu, 360 stepeni u krugu. Indusno–arapski brojni sistem, osnova-10, je najšire korišćeni sistem na svetu danas za većinu proračuna.
Istorija
[уреди | уреди извор]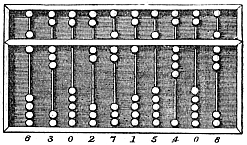
U današnje vreme je decimalni sistem sveprisutan. Njegov nastanak je verovatno bio inspirisan brojem prstiju. Međutim i niz drugih osnova je korišten u prošlosti, i dalje se koristi danas. Na primer, Vavilonski numerički sistem je imao osnovu 60, ali mu je nedostajala vrednosti 0. Nula je indicirana prostorom između brojeva. Do 300. p. n. e. interpunkcioni simbol (dva zakošena klinasta znaka) je ušao u upotrebu za označavanje nule u Vavilonskom sistemu. Na pločicama koje su pronađene u Kišu (koje datiraju iz 700. p.n.e), pisar Bêl-bân-aplu je zapisao nule sa tri kuke, umesto dva zakošena znaka.[1] Vavilonska oznaka nije bila nula u današnjem smislu reči, jer nije korišćena samostalno, niti je korištena na kraju broja. Stoga su brojevi poput 2 i 120 (2×60), 3 i 180 (3×60), 4 i 240 (4×60), izgledali isto, jer je velikim brojevima nedostajala krajnja seksagezimalna oznaka. Oni su se jedino mogli diferecirati u datom kontekstu.
Polimat Arhimed (ca. 287–212 BC) je izumeo decimalni pozicioni sistem u svom radu Psammites, koji je bio baziran na 108[2], što je kasnije navelo nemačkog matematičara Karla Gausa da jadikuje za nivoom koji bi nauka već bila dosegla do njegovog doba da je Arhimed ostvario pun potencijal svog genijalnog izuma.[3]
Pre nego što je poziciona notacija postala standard, jednostavni aditivni sistemi poput rimskih brojeva su korišćeni, i računovođe u antičkom Rimu i tokom Srednjeg veka su koristili abakus ili kamene brojače da rade aritmetiku.[4]

Horizontalna forma donjeg reda
Štapovi za brojanje i većina abakusa korišćeni su za predstavljanje brojeva u pozicionom numeričkom sistemu. Pomoću štapova za brojanje ili abakusa za izvođenje aritmetičkih operacija, pisanje početnih, srednjih i konačnih vrednosti proračuna može se lako obaviti jednostavnim sistemom aditiva u svakoj poziciji ili koloni. Ovaj pristup nije zahtevao pamćenje tabela (kao i poziciona notacija) i mogao je brzo da proizvede praktične rezultate.
Najstariji postojeći sistem pozicionih oznaka je bilo onaj kineskih štapićastih brojeva, koji se koriste najmanje od ranog 8. veka, ili možda kmerskih brojeva, koji pokazuju moguću upotrebu pozicionih brojeva u 7. veku. Kmerski brojevi i drugi indijski brojevi potiču od brahmanskih brojeva iz oko 3. veka pre nove ere, čiji se simboli u to vreme nisu koristili poziciono. Srednjovekovni indijski brojevi su pozicioni, kao i izvedeni arapski brojevi, zabeleženi od 10. veka.
Posle Francuske revolucije (1789–1799), nova francuska vlada je promovisala proširenje decimalnog sistema.[5] Neki od tih prodecimalnih napora — kao što su decimalno vreme i decimalni kalendar — bili su neuspešni. Drugi francuski prodecimalni napori - decimalizacija valute i metrika težina i mera - proširili su se iz Francuske na skoro ceo svet.
Istorija pozicionih razlomaka
[уреди | уреди извор]J. Lenart Bergren primećuje da je pozicione decimalne razlomke prvi put upotrebio arapski matematičar El-Uklidisi još u 10. veku.[6] Jevrejski matematičar Imanuel Bonfils koristio je decimalne razlomke oko 1350. godine, ali nije razvio notaciju koja bi ih predstavljala.[7] Persijski matematičar Jamšid al-Kaši napravio je isto otkriće decimalnih razlomaka u 15. veku.[6] Muhamed el Horezmi je uveo frakcije u islamske zemlje početkom 9. veka; njegova prezentacija razlomaka bila je slična tradicionalnim kineskim matematičkim razlomcima iz Suenci Suanđinga.[8] Ovaj oblik razlomka sa brojilcem na vrhu i imeniocem na dnu bez horizontalne trake takođe su koristili El-Uklidisi iz 10. veka i delo Džamšida el-Kašija iz 15. veka „Aritmetički ključ”.[8][9]
Usvajanje decimalnog predstavljanja brojeva manjih od jedan, razlomka, često se pripisuje Simonu Stevinu kroz njegov udžbenik De Thiende;[10] mada Stevin i E. J. Dijksterhuis ukazuju da je Regiomontanus doprineo evropskom usvajanju opštih decimala:[11]
- Evropski matematičari, kada su od Hindusa, preko Arapa, preuzeli ideju o pozicionoj vrednosti za cele brojeve, zanemarili su da ovu ideju prošire na razlomke. Nekoliko vekova oni su se ograničavali na upotrebu običnih i seksagezimalnih razlomaka... Ova polovičnost nikada nije u potpunosti prevaziđena, a seksagezimalni razlomci i dalje čine osnovu naše trigonometrije, astronomije i merenja vremena. ... Matematičari su nastojali da izbegnu razlomke uzimajući radijus R jednak broju jedinica dužine oblika 10n, a zatim su pretpostavili za n toliku integralnu vrednost da su sve veličine koje se pojavljuju mogle da se izraze sa dovoljnom tačnošću celim brojevima. Prvi je primenio ovu metodu nemački astronom Regiomontanus. U meri u kojoj je izrazio goniometrijske segmente linija u jedinici R/10n, Regiomontanus se može nazvati anticipatorom doktrine decimalnih pozicionih razlomaka.[11]:17,18
Po Dijksterhuisovoj proceni, „nakon objavljivanja De Thiende bio je potreban samo mali napredak da bi se uspostavio kompletan sistem decimalnih pozicionih razlomaka, i ovaj korak su odmah preduzeli brojni pisci... pored Stevina najznačajnija figura u ovom razvoju bio je Regiomontanus“. Dijksterhuis je primetio da [Stevin] „pripisuje puno priznanje Regiomontanu za njegov prethodni doprinos, rekavši da trigonometrijske tabele nemačkog astronoma zapravo sadrže celu teoriju 'brojeva desetne progresije'.[11]:19
Nepozicioni sistemi brojeva
[уреди | уреди извор]Osnovna karakteristika nepozicionih sistema brojeva je da simboli koji označavaju cifre imaju istu vrednost na različitim mestima u zapisu broja. Nama najpoznatiji nepozicioni sistem brojeva je rimski sistem brojeva. Pored njega, tu su egipatski brojni sistem i brojni sistem Maja.
Rimski sistem brojeva (200 godina p. n. e.) je aditivan sistem brojeva. Simboli ovog sistema su prikazani u sledecoj tabeli:
| Čitanje rimskih brojeva | Čitanje egipatskih brojeva | Čitanje brojeva Maja | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Pravila za pisanje
[уреди | уреди извор]Nikad se ne koristi niz koji ima više od tri identična simbola.
Ako je manja vrednost iza veće vrednosti, te dve vrednosti se sabiraju.
Ako je manja vrednost ispred veće vrednosti, oduzimanjem manje od veće vrednosti dobija se vrednost broja. Oduzimanje može da se vrši samo za vrednosti koje su umnošci 1, 10, 100 (I, X i C respektivno). Oduzimanje se vrši za sledeće simbole:
- I se oduzima od V i X; X se oduzima od L i C; C se oduzima od D i M.
Za vrednosti preko 3999 koristila se crta za nadvlačenje da se ukaze na množenje sa 1000. Ipak, Rimljani su retko pisali velike brojeve, tako da danas postoje neslaganja kad je u pitanju ovakav način zapisa velikih brojeva u ovom brojnom sistemu.
Reference
[уреди | уреди извор]- ^ Kaplan, Robert (2000). The Nothing That Is: A Natural History of Zero. Oxford: Oxford University Press.
- ^ „Greek numerals”. Архивирано из оригинала 26. 11. 2016. г. Приступљено 3. 2. 2017.
- ^ Menninger, Karl (1979). Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl. Vandenhoeck & Ruprecht. стр. 150—153. ISBN 978-3-525-40725-7.. Vandenhoeck und Ruprecht, 3rd. ed.
- ^ Ifrah, стр. 187
- ^ L. F. Menabrea. Translated by Ada Augusta, Countess of Lovelace. "Sketch of The Analytical Engine Invented by Charles Babbage" Архивирано 15 септембар 2008 на сајту Wayback Machine. 1842.
- ^ а б Berggren, J. Lennart (2007). „Mathematics in Medieval Islam”. The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. стр. 518. ISBN 978-0-691-11485-9.
- ^ Gandz, S.: The invention of the decimal fractions and the application of the exponential calculus by Immanuel Bonfils of Tarascon (c. 1350). Sarton, George; Gandz, Solomon (1936). „The Invention of the Decimal Fractions and the Application of the Exponential Calculus by Immanuel Bonfils of Tarascon (C. 1350)”. Isis. 25: 16—45. doi:10.1086/347058..
- ^ а б Lam Lay Yong, "The Development of Hindu-Arabic and Traditional Chinese Arithmetic", Chinese Science, 1996 pp. 38, Kurt Vogel notation
- ^ Lay Yong, Lam. „A Chinese Genesis, Rewriting the history of our numeral system”. Archive for History of Exact Sciences. 38: 101—108.
- ^ B. L. van der Waerden (1985). A History of Algebra. From Khwarizmi to Emmy Noether
 . Berlin: Springer-Verlag.
. Berlin: Springer-Verlag.
- ^ а б в E. J. Dijksterhuis (1970) Simon Stevin: Science in the Netherlands around 1600, Martinus Nijhoff Publishers, Dutch original 1943
Literatura
[уреди | уреди извор]- O'Connor, John; Robertson, Edmund (2000). „Babylonian Numerals”. Архивирано из оригинала 11. 09. 2014. г. Приступљено 21. 8. 2010.
- Kadvany, John (2007). „Positional Value and Linguistic Recursion”. Journal of Indian Philosophy. 35 (5–6): 487—520. S2CID 52885600. doi:10.1007/s10781-007-9025-5.
- Knuth, Donald (1997). The art of Computer Programming. 2. Addison-Wesley. стр. 195—213. ISBN 978-0-201-89684-8.
- Ifrah, George (2000). The Universal History of Numbers: From Prehistory to the Invention of the Computer. Wiley. ISBN 978-0-471-37568-5.
- Kroeber, Alfred (1976). Handbook of the Indians of California. Courier Dover Publications. стр. 176. ISBN 9780486233680. Непознати параметар
|orig-date=игнорисан (помоћ) - J.P. Mallory and D.Q. Adams, Encyclopedia of Indo-European Culture, Fitzroy Dearborn Publishers, London and Chicago, 1997.
- Nissen, Hans J.; Damerow, Peter; Englund, Robert K. (1993). Archaic Bookkeeping: Early Writing and Techniques of Economic Administration in the Ancient Near East. University of Chicago Press. ISBN 978-0-226-58659-5.
- Schmandt-Besserat, Denise (1996). How Writing Came About. University of Texas Press. ISBN 978-0-292-77704-0.
- Zaslavsky, Claudia (1999). Africa counts: number and pattern in African cultures. Chicago Review Press. ISBN 978-1-55652-350-2.
- Florian Cajori, (1929), 2 volumes. Cajori, Florian (јануар 1993). A History of Mathematical Notations. Courier Corporation. ISBN 0-486-67766-4.
- Mazur, Joseph (6. 12. 2016). Enlightening Symbols: A Short History of Mathematical Notation and Its Hidden Powers. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-15463-3.
- „Decimal point definition and meaning | Collins English Dictionary”. www.collinsdictionary.com (на језику: енглески). Приступљено 2018-07-05.
- Weisstein, Eric W. „Decimal Point”. mathworld.wolfram.com (на језику: енглески). Приступљено 2020-08-22.
- „decimal point Meaning in the Cambridge English Dictionary”. dictionary.cambridge.org (на језику: енглески). Приступљено 2018-07-05.
- „How to Change Excel's Decimal Separators from Periods to Commas” (на језику: енглески). Приступљено 2018-07-05.
- „Decimal Separators: Points or commas? - Elementary Math”. Elementary Math (на језику: енглески). 2018-01-19. Приступљено 2018-07-05.
- „Definition of Decimal Point”. www.mathsisfun.com. Приступљено 2020-08-22.
- „Mythematics: a decimal point”. Grammarphobia (на језику: енглески). 2012-02-17. Приступљено 2018-07-05.


