Функција расподеле простих бројева

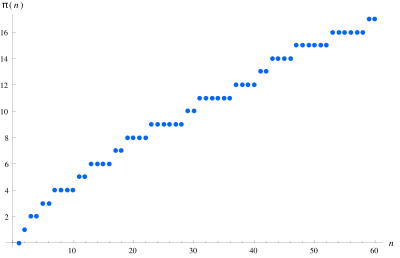
У математици, функција расподеле простих бројева је функција расподеле броја простих бројева мањих или једнаких некој стварном броју x. Означава се $\scriptstyle \pi (x)$ (неповезани са бројем π).

Вредности π(n) за првих 60 целих бројева

Историја

Од великог интересовања у теорији бројева је стопа раста функције расподеле простих бројева. То су претпоставили крајем 18. века Гаус и Лежандр да буде приближно

$x/\operatorname {ln} (x)\!$

у смислу да

$\lim _{x\rightarrow \infty }{\frac {\pi (x)}{x/\operatorname {ln} (x)}}=1.\!$

Овај израз је теорема простих бројева. Еквивалентни израз је

$\lim _{x\rightarrow \infty }\pi (x)/\operatorname {li} (x)=1\!$

где јеli је логаритамска интегрална функција. Теорему простих бројева је први пут доказао 1896. године Жак Адамард и Чарлс де ла Вале Пусон самостално, користећи својства Риманове зета функције коју је увео Риман 1859. године.

Прецизније процене $\pi (x)\!$ које су сада познате; на пример

$\pi (x)=\operatorname {li} (x)+O{\bigl (}xe^{-{\sqrt {\ln x}}/15}{\bigr )}\!$

где је О је бележење за велико О. За већину вредности $x$ ми смо заинтересовани за (то јест, када $x$ није неразумно велики) $\operatorname {li} (x)\!$ је већи од $\pi (x)\!$, али бескрајно често је супротно. За расправу о томе, погледај Скјуесов број.

Докази о теореми простих бројева не користе зета функцију или сложене анализе које су пронађени око 1948. године Атл Селберг и Пол Ердош(у највећој мери независно).

Табеле π(x), x / ln x, и li(x)

Табела приказује како су три функције π(x), x / ln x и li(x) упоређујуће на степен 10. Види још,иd

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)
10	4	−0.3	2.2	2.500
102	25	3.3	5.1	4.000
103	168	23	10	5.952
104	1,229	143	17	8.137
105	9,592	906	38	10.425
106	78,498	6,116	130	12.740
107	664,579	44,158	339	15.047
108	5,761,455	332,774	754	17.357
109	50,847,534	2,592,592	1,701	19.667
1010	455,052,511	20,758,029	3,104	21.975
1011	4,118,054,813	169,923,159	11,588	24.283
1012	37,607,912,018	1,416,705,193	38,263	26.590
1013	346,065,536,839	11,992,858,452	108,971	28.896
1014	3,204,941,750,802	102,838,308,636	314,890	31.202
1015	29,844,570,422,669	891,604,962,452	1,052,619	33.507
1016	279,238,341,033,925	7,804,289,844,393	3,214,632	35.812
1017	2,623,557,157,654,233	68,883,734,693,281	7,956,589	38.116
1018	24,739,954,287,740,860	612,483,070,893,536	21,949,555	40.420
1019	234,057,667,276,344,607	5,481,624,169,369,960	99,877,775	42.725
1020	2,220,819,602,560,918,840	49,347,193,044,659,701	222,744,644	45.028
1021	21,127,269,486,018,731,928	446,579,871,578,168,707	597,394,254	47.332
1022	201,467,286,689,315,906,290	4,060,704,006,019,620,994	1,932,355,208	49.636
1023	1,925,320,391,606,803,968,923	37,083,513,766,578,631,309	7,250,186,216	51.939
1024	18,435,599,767,349,200,867,866	339,996,354,713,708,049,069	17,146,907,278	54.243
1025	176,846,309,399,143,769,411,680	3,128,516,637,843,038,351,228	55,160,980,939	56.546
1026	1,699,246,750,872,437,141,327,603	28,883,358,936,853,188,823,261	155,891,678,121	58.850

График показује однос функције расподеле простих бројева π(x)до две своје апроксимације, x/ln x и Li(x). Као x расте ( напомена x оса је логаритамска), оба односа нагињу ка 1. Однос за x/ln x конвергира одозго врло споро, док је однос за Li(x) конвергира брже одоздо.

У онлајн енциклопедији целих секвенци, π(x)Колона је секвенца А006880 π(x) - x / ln x је секвенц  A057835, и li(x) − π(x) је секвенца  A057752.

Вредност за π(10²⁴)су првобитно израчунава Ј. Ботх, Ј. Франке, А. Џост, и Т. Клејњунг под претпоставком Риманове хипотезе. Касније је проверио безусловним израчунавањем Д. Ј. Плат. За вредност π(10²⁵)је због Ј. Ботх, Ј. Франке, А. Џост, и Т. Клеињунг. За вредност π(10²⁶)израчунао је Д. Б. Стапл. Сви остали уписи у овој табели су верификовани као делови тог посла.

Алгоритми за вредновање π(x)

Једноставан начин да се пронађе $\pi (x)$, ако $x$ није превелико, је да се користи Ератостеново сито и произведу прости бројеви мањи или једнаки$x$а затим их пребројати.

Подробнији начин проналажења$\pi (x)$ је због Лежандреја: дато $x$, ако $p_{1},p_{2},\ldots ,p_{n}$ су различити прости бројеви, онда је број целих бројева мањи или једнак $x$који су недељиви са $p_{i}$ је

$\lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots$

(где $\lfloor \cdots \rfloor$ означава спрат функцију). Овај број је стога једнак

$\pi (x)-\pi \left({\sqrt {x}}\right)+1$

када бројеви $p_{1},p_{2},\ldots ,p_{n}$ су прости бројеви мањи или једнаки од кв.корена $x$.

У серији текстова објављених између 1870. и 1885. године Ернест Мејсел описује (и користи) практичан начин вредновања комбинаторног $\pi (x)$. Let $p_{1}$, $p_{2},\ldots ,p_{n}$ где први $n$ прости бројеви и означавају стране $\Phi (m,n)$број природних бројева не већи о $m$ који нису дељив са $p_{i}$. Тада

$\Phi (m,n)=\Phi (m,n-1)-\Phi \left({\frac {m}{p_{n}}},n-1\right)$

Датје природан број $m$, ако $n=\pi \left({\sqrt[{3}]{m}}\right)$ и ако $\mu =\pi \left({\sqrt {m}}\right)-n$, тада

$\pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right)$

користећи овај приступ, Мејсел је израчунао $\pi (x)$, за $x$ једнако 5×10⁵, 10⁶, 10⁷, и 10⁸.

Године 1959, Дерик Хенри Лехмер је проширио и поједноставио Мејселобу методу. Дефинисати, за реалан $m$ и за природне бројев $n$ и $k$, $P_{k}(m,n)$ као број бројева није већи од m са тачно k простим чиниоцем, бољим од $p_{n}$. Осим тога, комплет $P_{0}(m,n)=1$. Тада

$\Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n)$

где збир заправо има само коначно много различитих од нула услове. $y$означава цео број такав да је ${\sqrt[{3}]{m}}\leq y\leq {\sqrt {m}}$, и склоп $n=\pi (y)$. Тада $P_{1}(m,n)=\pi (m)-n$ и $P_{k}(m,n)=0$ када $k$ ≥ 3. Стога

$\pi (m)=\Phi (m,n)+n-1-P_{2}(m,n)$

Прорачун $P_{2}(m,n)$може се добити на овај начин:

$P_{2}(m,n)=\sum _{y<p\leq {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right)$

С друге стране, рачунање $\Phi (m,n)$ може бити урађено користећи следећа правила:

1. $\Phi (m,0)=\lfloor m\rfloor$
2. $\Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)$

Користећи свој метод и IBM 701, Лехмер је могао да израчуна $\pi \left(10^{10}\right)$.

Даљи напредак ове метода су направили Лагаријас, Милер, Одлиско, Делеглиз и Риват.

Друге функције расподеле простих бројева

Друге функције расподеле простих бројева се користе јер су погодније за рад. Једна је Риманова функција расподеле простих бројева, обично означена као $\Pi _{0}(x)$или $J_{0}(x)$. Овај скок 1/n за просте степене pⁿ, уз то узимање вредности на пола пута између две стране у дисконтинуитету. Детаљ је додат јер онда може бити дефинисан од стране супротности. Мелин га је преобразио. Формално, можемо дефинисати $\Pi _{0}(x)$ као

$\Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )}$

где је p прост број. 

Могуће је и написати

$\Pi _{0}(x)=\sum _{2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}(x^{1/n})$

гдеје Λ(n) вон Манголдотова функција и 

$\pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.$

Мебијусова инверзна формула даје

$\pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}(x^{1/n})$

Знајући однос између Риманове зета функције и вон Манголдотове функције  $\Lambda$, и коришћењем Перонове формуле имамо

$\ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\,dx$

Чебишева функција тежине простих бројева или простих степена pⁿ од ln(p):

$\theta (x)=\sum _{p\leq x}\ln p$

$\psi (x)=\sum _{p^{n}\leq x}\ln p=\sum _{n=1}^{\infty }\theta (x^{1/n})=\sum _{n\leq x}\Lambda (n).$

Пиманова функција расподеле простих бројева има обичну производну функцију која се може изразити у смислу формалне серије степена као:

$\sum _{n=1}^{\infty }\Pi _{0}(n)x^{n}=\sum _{a=2}^{\infty }{\frac {x^{a}}{1-x}}-{\frac {1}{2}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }{\frac {x^{ab}}{1-x}}+{\frac {1}{3}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }{\frac {x^{abc}}{1*x}}-{\frac {1}{4}}\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }\sum _{d=2}^{\infty }{\frac {x^{abcd}}{1-x}}+\cdots$

Формуле за функције расподеле простих бројева

Формула за функције расподеле простих бројева се јављају у две врсте: аритметичке формула и аналитичке формула. Аналитичке формуле за расподелу простих бројева биле су први пут употребљене да се докаже проста теорема бројева. Оне произилазе из Римановог и вон Манголдотовог рада, и опште су позната као експлицитне формуле.

Имамо следећи израз за ψ:

$\psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\ln 2\pi -{\frac {1}{2}}\ln(1-x^{-2})$

где 

$\psi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.$

Овде ρ су нуле Риманова зета функција у критичној траци, где је права дели ρ је између нула и јединице. Формула важи за вредности xвећи од један, што је област интересовања. Износ по корену је условно конвергира, а треба узети у циљу повећања апсолутну вредност имагинарног дела. Имајте на уму да исту сума над тривијалним кореновима даје последње одузимање у формули.

за $\scriptstyle \Pi _{0}(x)$ имамо више сложену формулу

$\Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\ln 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\ln t}}.$

Поново, формула је валидна за x > 1, док  ρ су нетривијалне нуле зета функције према њиховој апсолутној вриједности, а, опет, други интегрални, узет са минус знаком, је исто сума, али током тривијалних нула. Први термин li(x)је уобичајена логаритамска интегрална функција; израз li(x^ρ) у другом термину треба сматрати Ei(ρ ln x), где Ei је аналитички наставак експоненцијалне интегралне функције из позитивних реалних бројева у комплексној равни са гране дуж негативних реалних бројева.

Дакле Мебијусова инверзна функција нам даје

$\pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho })-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}$

за x > 1, где

$\operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k!k\zeta (k+1)}}$

је такозвана Риманова Р-функција. Последња серија која је позната је Грамова серија  и конвергира за све позитивн x.

Збир свих нетривијалних зета нула у формули за $\scriptstyle \pi _{0}(x)$ описује флустрације $\scriptstyle \pi _{0}(x)$, док  преостали термини дају "углађене" делове функције расподеле простих бројева, па може се користити

$\operatorname {R} (x)-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}$

као најбољи естиматор $\scriptstyle \pi (x)$ за x > 1.

Амплитуда "буке" је хеуристички део о $\scriptstyle {\sqrt {x}}/\ln x$, тако да флуктуације расподеле простих бројева могу бити јасно представљене са Δ-функцијом:

$\Delta (x)=\left(\pi _{0}(x)-\operatorname {R} (x)+{\frac {1}{\ln x}}-{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}\right){\frac {\ln x}{\sqrt {x}}}.$

Вредносна табела Δ(x) је доступна.

Неједнакости

Ово су неке неједнакости за π(x).

${\frac {x}{\ln x}}<\pi (x)<1.25506{\frac {x}{\ln x}}\!$за x ≥ 17.

Лева неједнакост прати за  x ≥ 17 и десна неједнакост прати за x > 1.  

Објашњење константе 1.25506 дато је као (секвенца А209883 у ОЕИС)

Пјер Дурсат је доказао 2010 године:

${\frac {x}{\ln x-1}}<\pi (x)$ за $x\geq 5393$, и

$\pi (x)<{\frac {x}{\ln x-1.1}}$ за $x\geq 60184$.

Ово су неке неједнакости за n-ти просте бројеве, p_n.

$n(\ln(n\ln n)-1)<p_{n}<n{\ln(n\ln n)}\!$ за n ≥ 6.

Лева неједнакост показује за n ≥ 1 и десна неједнакост показује за  n ≥ 6.

Апроксимација за n-ти прост број је

$p_{n}=n(\ln(n\ln n)-1)+{\frac {n(\ln \ln n-2)}{\ln n}}+O\left({\frac {n(\ln \ln n)^{2}}{(\ln n)^{2}}}\right).$

Риманова хипотеза

Риманова хипотеза је еквивалнтна много чвршћим везаним грешкама у процени за $\pi (x)$, и стога је више ка редовној дистрибуцији простих бројева,

$\pi (x)=\operatorname {li} (x)+O({\sqrt {x}}\log {x}).$

Види још

• Бертранов постулат
• Ојлерова претпоставка
• Foias constant

Спољашње везе

• Chris Caldwell, The Nth Prime Page at The Prime Pages.
• Tomás Oliveira e Silva, Tables of prime-counting functions.