Пређи на садржај

Брзина светлости

Уреди везе
С Википедије, слободне енциклопедије
(преусмерено са Speed of light)
Брзина светлости
alt = The distance from the Sun to the Earth is shown as 150 million kilometers, an approximate average. Sizes to scale.
Сунчевој свјетлости је потребно око 8 минута и 17 секунди да пређе просечно растојање од површине Сунца до Земље.
Тачне вредности
метара у секунди299792458
Планкова дужина по Планковом времену
(i.e., Планкове јединице)		1
Приближне вредности (до три значајне цифре)
Километара на сат1080 милион (1,08×109)
миља по секунди186000
миља по сату[1]671 милион (6,71×108)
астрономских јединица на дан173[Note 1]
парсека годишње0,307[Note 2]
Приближно време путовања светлосног сигнала
РастојањеВреме
једна стопа1,0 ns
један метар3,3 ns
од геостационарне орбите до Земље119 ms
дужина Земљиног екватора134 ms
од Месеца до Земље1,3 s
од Сунца до Земље (1 АУ)8,3 мин
једна светлосна година1,0 година
један парсек3,26 година
од најближе звезде до Сунца (1,3 pc)4,2 година
од најближе галаксије (патуљасте галаксије Велики пас) до Земље25,000 година
преко Млечног пута100,000 година
од галаксије Андромеда до Земље2,5 милиона година
од Земље до краја видљивог свемира46,5 милијарди година

Брзина светлости у вакууму износи тачно 299.792.458 m/s (приближно 300.000 km/s), односно 1.079.252.848,8 km/h, представља важну физичку константу и зато се обележава посебним словом c (од латинске речи celeritas). У теорији релативности, c међусобно повезује простор и време, а исто тако се јавља у познатој једначини једнакости масе и енергије E = mc2.[2] У различитим срединама (течностима, гасовима итд.) брзина светлости је различита и увек мања него у вакууму.[3] С обзиром да је светлост облик електромагнетног зрачења, њена брзина зависи од електричних и магнетних својстава средине кроз коју се креће и константна је за ту средину.[4] Израчунава се на основу формуле: . У вакууму је .

Брзина светлости је један од важнијих појмова у Ајнштајновој теорији релативности. Према истој теорији није могуће кретање брзинама већим од брзине светлости у вакууму.[5]

Прву познату и признату историјску методу за мерење брзине светлости извео је дански астроном Оле Кристенсен Ремер 1675. године. После Ремера, Физо без астрономских метода долази до брзине светлости која износи 313.870 km/s.

Најпознатије мерење брзине је извео Алберт Мајкелсон, уз помоћ ротирајућих огледала у Калифорнији. Захваљујући тим експериментима, утврђено је да је брзина светлости 299.792,458 km/s, а сам Мајкелсон је добио Нобелову награду 1907.

С обзиром да се основна мерна јединица за време (секунда) може прецизније измерити од основне јединица за дужину, метра, брзина светлости је искоришћена за прецизну дефиницију ове мерне јединице. Тако је од 21. октобра 1983. године метар одређен као растојање које светлост пређе у вакууму за 1/299.792.458 део секунде.[6]

Нумеричка вредност, нотација, и јединице

[уреди | уреди извор]

Врзина светлости у вакууму се обично означава малим словом c, за constant" или лат. celeritas (са значењем „брзина“). Године 1856, Вилхелм Едуард Вебер и Рудолф Колрауш су користили c за различите константе за које је касније показано да су једнаке √2 пута брзина светлости у вакууму. Историјски, симбол V је кориштен као алтернативни симбол за брзину светлости, који је увео Џејмс Клерк Максвел 1865. године. Пол Друд је 1894. године редефинисао симбол c у његово садашње значење. Ајнштајн је користио V у својим оригиналним публикацијама на немачком о специјалној релативности 1905, али је 1907. прешао на c, које је у то време постало стандардни симбол за брзину светлости.[7][8]

Понекад се c користи за брзину таласа у било ком материјалном медију, а c0 за брзину светлости у вакууму.[9] Ова усвојена нотација, која је подржана у званичној СИ литератури,[6] има исту форму као и друге сродне константе: наиме, μ0 за пермеабилност вакуума или магнетна константа, ε0 за диелектричну константу вакуума или електричну константу, и Z0 за отпорност простора. Овај чланак искључиво користи c за брзину светлости у вакууму.

Од 1983, метар је дефинисан у Међународном систему јединица (СИ) као растојање које светлост пређе у вакууму за 1⁄299792458 секунди. Ова дефиниција подразумева брзину светлости у вакууму на тачно 299,792,458 m/s.[10][11][12] Као димензиона физичка константа, нумеричка вредност c се разликује за различите системе јединица. Брзина светлости у империјалним (британским) јединицама и САД јединицама је базирана на инчу са тачно 2,54 cm и њена вредности је тачно 186.282 миља, 698 јарди, 2 стопе, и 5+21/127 инча по секунди.[13] У гранама физике у којима се c често јавља, као што је теорија релативности, уобичајено се користе системи природних јединица кретања или геометријски систем јединица где c = 1.[14][15] Користећи ове јединице, c се не појављује експлицитно пошто множење или дељење са 1 не утиче на резултат.

Историја

[уреди | уреди извор]

Пре првих научних покушаја мерења брзине светлости, у старој Грчкој код Хераклита и Емпедокла постојало је мишљење да је светлост некакво испаравање, или исијавање, али је постојала разлика између неких (као Емпедокло) који су мислили да се светлост креће тако брзо да ту брзину само није могуће мерити и других (као Аристотел) који су говорили да се светлост шири простором тренутно (бесконачно брзо).[16]

После, у новом веку мишљење да се светлост креће бесконачном брзином била је сумњива Галилеју и он је покушао, помоћу телескопа, да одреди брзину светлости, али је удаљеност од неколико километара, на коју је био поставио светиљке била је мала да се одреди брзина светлости.[17]

Ремеров покушај мерења

[уреди | уреди извор]
Скица Ремеровог метода за одређивање брзине светлости на основу кашњења заласка Јупитеровог месеца Ио

Дански астроном Оле Кристенсен Ремер је 1675. установио да тренуци опажања окултација (кад се небеско тело, гледано са Земље, скрива иза другог) Јупитерових сателита (пример је Ио) зависе од брзине ширења светлости. До тада се сматрало да се светлост шири бесконачном брзином. Када се Земља налази у положају 1. (види слику доле), посматрач уочава да до окултација долази у једнаким временским размацима, тада се Земља нити приближава нити удаљава од Јупитера. У положају 2. Земља се удаљава од Јупитера, а посматрач налази да тренуци окултације касне. Разлог је у томе што је светлости потребно додатно време да превали повећану удаљеност до Земље. Знајући у којим су се размацима времена окултације појављивале у положају 1, може се предвидети време окултације када се дође у положају 3. Међутим до ње не би долазило још толико времена колико је светлости потребно да превали удаљеност од положаја Земље 1. до положаја Земље 3, а то је дужина 2а. Ремер је измерио да укупно кашњење износи око t = 1,000 секунди. За брзину светлости следи:[18]

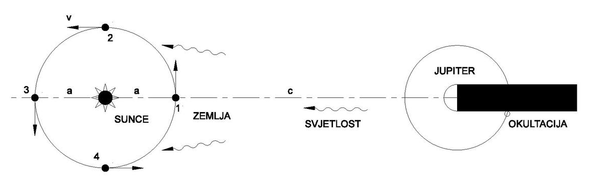
Астрономска метода мерења брзине светлости

где је: c – брзина светлости, a – удаљеност Земље од Сунца, t – време кашњења светлости.

Бројна вредност брзине светлости директно зависи од тачности с којом је позната средња удаљеност до Сунца (у оно време позната као 140 милиона километара). Однос брзине светлости и брзине Земље не зависи од средње удаљености до Сунца. Наиме, како је брзина кретања Земље по стази једнака v = 2aπ / Z, где је Z сидеричка година, то је:

где је: c – брзина светлости, v = брзина кретања Земље, a – удаљеност Земље од Сунца, Z - сидеричка година Земље, π = 3.14, t – време кашњења светлости.

Ремер је вршио мерења око 8 година и однос c : v је изашао око 7600. Данашње вредности су 299.792 km/s : 29,8 km/s ≈ 10,100. У ствари Ремер није направио никакав прорачун и није проценио брзину светлости. На основу његових мерења то је обавио Кристијан Хајгенс и он је добио за око 25% мању вредност од данашњих мерења. Значајно је да је Ремер доказао да је брзина светлости коначна. Његови резултати нису у почетку прихваћени, све док Џејмс Бредли 1727. није открио аберацију светлости. Године 1809. француски астроном Жан-Батист-Жозеф Деламбр је поновио Ремерова мерења, која су тада обављена с много тачнијим мерним инструментима и добио за брзину светлости око 300.000 km/s. Он је у ствари измерио да светлост путује са Сунца до Земље 8 минута и 12 секунди (стварна вредност је 8 минута и 19 секунди).

Мерења на Земљи

[уреди | уреди извор]

Главни проблем с првим земаљским (терестричким) мерењима је био што су научници у експериментима могли да проучавају распростирање светлости на релативно малим удаљеностима.

Први важнији покушај је спровео Иполит Физо помоћу уређаја с ротирајућим зупчаником кроз чије зупце је пропуштао светлост. Мерењима је добио вредност од око 313.300 km/s.

Амерички физичар Мајкелсон за своја је мерења светлости у раздобљу од 1880. до 1920. примио Нобелову награду за физику. Користио се осмостаничним ротирајућим огледалом и извором светлости удаљеним око 35 km. Својим мерењима је добио вредност од око 300.000 km/s.

После је с колегом Едвардом Морлејем спровео Мајкелсон—Морлијев експеримент, у којем су доказали да брзина светлости не зависи од извора, нити од брзине кретања извора.

Савремена мерења су утврдила брзину светлости на тачно 299.792.458 m/s.

Улога у физици

[уреди | уреди извор]

Гранична брзина

[уреди | уреди извор]

Према посебној теорији релативности, енергија предмета масе m и брзине v дата је једначином γmc2, где је γ Лоренцов фактор. Ако тело мирује, v је једнака нули, па је γ једнак 1, из чега следи E = mc2, којим се дефинише еквиваленција масе и енергије. γ се приближава бесконачности како се v приближава c, па би била потребна бесконачна количина енергије како би објект масе m достигао брзину светлости. Другим речима, маса m тела које мирује мања је од масе m0 тела које се креће: у складу са формулом . То значи да што је тело брже, и што се више приближава брзини светлости, треба му све више енергије како би своју, све већу масу, успело да убрза. Брзина светлости је тиме горња граница брзине за објекте који посједују масу, па због тога појединачни фотони не могу путовати брзинама већим од брзине светлости.[19][20] Ово је експериментално доказано у многим тестирањима релативистичке енергије и момента.[21]

Напомене

[уреди | уреди извор]
  1. ^ Тачна вредност:
    (299792458 × 60 × 60 × 24 / 149597870700) АУ/дан
  2. ^ Тачна вредност:
    999992651π/10246429500 pc/y

Референце

[уреди | уреди извор]
  1. ^ Larson & Hostetler 2007, стр. 197.
  2. ^ Uzan, J-P; Leclercq, B (2008). The Natural Laws of the Universe: Understanding Fundamental Constants. Springer. стр. 43—4. ISBN 978-0-387-73454-5. 
  3. ^ Penrose, R (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage Books. стр. 410—11. ISBN 978-0-679-77631-4. „... the most accurate standard for the metre is conveniently defined so that there are exactly 299.792.458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris.” 
  4. ^ „How is the speed of light measured?”. Архивирано из оригинала 21. 8. 2015. г. 
  5. ^ Stachel 2002, стр. 226
  6. ^ а б International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th изд.), стр. 112, ISBN 92-822-2213-6 
  7. ^ Gibbs, P (2004) [1997]. „Why is c the symbol for the speed of light?”. Usenet Physics FAQ. University of California, Riverside. Архивирано из оригинала 17. 11. 2009. г. Приступљено 16. 11. 2009.  "The origins of the letter c being used for the speed of light can be traced back to a paper of 1856 by Weber and Kohlrausch [...] Weber apparently meant c to stand for 'constant' in his force law, but there is evidence that physicists such as Lorentz and Einstein were accustomed to a common convention that c could be used as a variable for velocity. This usage can be traced back to the classic Latin texts in which c stood for 'celeritas' meaning 'speed'."
  8. ^ Mendelson, KS (2006). „The story of c”. American Journal of Physics. 74 (11): 995—997. Bibcode:2006AmJPh..74..995M. doi:10.1119/1.2238887. 
  9. ^ See for example:
  10. ^ Sydenham, PH (2003). „Measurement of length”. Ур.: Boyes, W. Instrumentation Reference Book (3rd изд.). Butterworth–Heinemann. стр. 56. ISBN 978-0-7506-7123-1. „... if the speed of light is defined as a fixed number then, in principle, the time standard will serve as the length standard ...” 
  11. ^ „CODATA value: Speed of Light in Vacuum”. The NIST reference on Constants, Units, and Uncertainty. NIST. Приступљено 21. 8. 2009. 
  12. ^ Jespersen, J; Fitz-Randolph, J; Robb, J (1999). From Sundials to Atomic Clocks: Understanding Time and Frequency (Reprint of National Bureau of Standards 1977, 2nd изд.). Courier Dover. стр. 280. ISBN 978-0-486-40913-9. 
  13. ^ Savard, J. „From Gold Coins to Cadmium Light”. John Savard. Архивирано из оригинала 14. 11. 2009. г. Приступљено 14. 11. 2009. 
  14. ^ Lawrie, ID (2002). „Appendix C: Natural units”. A Unified Grand Tour of Theoretical Physics (2nd изд.). CRC Press. стр. 540. ISBN 978-0-7503-0604-1. 
  15. ^ Hsu, L (2006). „Appendix A: Systems of units and the development of relativity theories”. A Broader View of Relativity: General Implications of Lorentz and Poincaré Invariance (2nd изд.). World Scientific. стр. 427—8. ISBN 978-981-256-651-5. 
  16. ^ Логос 2017, стр. 22.
  17. ^ Логос 2017, стр. 274.
  18. ^ Владис Вујновић : "Астрономија", Школска књига, 1989.
  19. ^ It's official: Time machines won't work, Los Angeles Times, pristupljeno 25. јула 2011., pristupljeno 8. decembra 2016.
  20. ^ HKUST Profesori dokazali da fotoni ne nadilaze brzinu svetlosti, pristupljeno 8. decembra 2016.
  21. ^ Fowler, M (март 2008). „Notes on Special Relativity” (PDF). University of Virginia. стр. 56. Приступљено 7. 5. 2010. 

Литература

[уреди | уреди извор]

Спољашње везе

[уреди | уреди извор]
Брзина светлости на Викимедијиној остави.
Преузето из „https://sr.wikipedia.org/w/index.php?title=Брзина_светлости&oldid=27680073”