Индекс преламања

Индекс преламања материјала је број који показује колико пута је брзина светлости у некој средини мања од брзине у вакууму. Преламање је најочигледнија манифестација промене брзине светлости (електромагнетног (ЕМ) зрачења) при преласку из једне средине у другу. Индекс преламања зависи од таласне дужине (фреквенције) светлости што се експериментално испољава у појави спектра када се зрак полихроматске (беле) светлости пропусти кроз призму. Индекс преламања је важна особина материјала и зато се брижљиво мери (рефрактометром) и табулира.
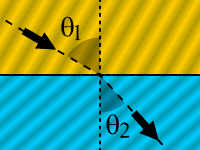
Индекс преламања одређује колико је путања светлости савијена или преломљена при уласку у материјал. Ово је описано Снеловим законом преламања, n1 sin θ1 = n2 sin θ2, где су θ1 и θ2 упадни и преламајући угао зрака који прелази границу између две средине са индексима преламања n1 и n2. Индекси преламања такође одређују количину светлости која се рефлектује када дође до интерфејса, као и критични угао за укупну унутрашњу рефлексију, њихов интензитет (Фреснелове једначине) и Брустеров угао.[1]
Индекс преламања се може посматрати као фактор за који се брзина и таласна дужина зрачења смањују у односу на њихове вакуумске вредности: брзина светлости у медијуму је v = c/n, а сходно томе и таласна дужина у том медијуму је λ = λ0/n, где је λ0 таласна дужина те светлости у вакууму. Ово имплицира да вакуум има индекс преламања 1 и претпоставља да на фреквенцију (f = v/λ) таласа не утиче индекс преламања.
Индекс преламања може варирати у зависности од таласне дужине. Ово узрокује да се бела светлост дели на саставне боје када се прелама. Ово се зове дисперзија. Овај ефекат се може посматрати у призмама и дугама, и као хроматска аберација у сочивима. Ширење светлости у апсорбујућим материјалима може се описати коришћењем индекса преламања комплексне вредности.[2] Имагинарни део тада управља слабљењем, док реални део узима у обзир преламање. За већину материјала индекс преламања се мења са таласном дужином за неколико процената у видљивом спектру. Ипак, индекси преламања за материјале се обично извештавају коришћењем једне вредности за n, која се обично мери на 633 nm.
Концепт индекса преламања примењује се на цео електромагнетни спектар, од рендгенских зрака до радио таласа. Такође се може применити на таласне појаве као што је звук. У овом случају се користи брзина звука уместо брзине светлости и мора се изабрати референтни медијум који није вакуум.[3]
Дефиниције
[уреди | уреди извор]Индекс преламања има много дубље значење поготову што може да се повеже са другим особинама материјала и сагласно томе може се дефинисати на више начина.[1]
Стриктно говорећи, индекс преламања је однос који показује за колико пута је фазна брзина електромагнетног (ЕМ) зрачења у њему, , мања у односу на брзину у вакууму, . Обично се обележава симболом , и за материјал дефинише као:
У материјалу са индексом преламања 1,5 = 3/2 брзина светлости износи тачно 2/3 брзине светлости у вакууму, приближно 300.000 km/s.
Пошто је брзина светлости (електромагнетних таласа) повезана са електричним и магнетним особинама материјала индекс преламања се еквивалентно може изразити и релацијом:
где је релативна (диелектрична) пермитивност материјала, а релативна (магнетна) пермеабилност. За немагнетне материјале је врло блиско јединици па је приближно једнако . Фазна брзина представља брзину којом се креће врх таласа, дакле, брзину којом се креће фаза таласа. Групна брзина је брзина којом путује обвојница таласа.
Брзина светлости
[уреди | уреди извор]Брзина простирања електромагнетних таласа у вакууму, c, је иста за све врсте зрачења и приближно износи 3×108 метара у секунди. Дакле, ако је v фазна брзина зрачења одређене фреквенције у датом материјалу, индекс преламања је дат изразом:
Овај број је типично већи од један: што је већи индекс преламања светлост се у материјалу спорије креће. Међутим, на неким фреквенцијама (рецимо у близини апсорпционе резонанције или код х-зрака) n постаје мање од јединице. То не противуречи теорији релативности према којој сигнал који носи информацију не може да се креће брзином већом од c, јер фазна брзина није иста као и групна брзина којом се информација преноси.
Понекад се дефинише и „индекс преламања групне брзине“, групни индекс:
где је vg групна брзина. Овај индекс не треба мешати са n који се увек односи на фазну брзину.
Смањење фазне брзине може се објаснити и класичном сликом на микроскопској скали. Променљиво електрично поље ЕМ таласа наводи на додатне осцилације наелектрисања у материјалу што се због њихове мале масе, углавном односи на електроне. Дакле, свеприсутни електрони (из атома и молекула од којих је сачињен материјал) осцилују под утицајем ЕМ таласа али због постојећих привлачних сила између електрона и атомских језгара, које се супротстављају поремећају, осцилације малко касне у односу на осцилације ЕМ таласа. Свако наелектрисање приликом промене брзине емитује сопствено зрачење, па тако и електрони који осцилују под утицајем ЕМ таласа. То зрачење има исту фреквенцију као и побудни ЕМ таласи, али мало касни у фази за ЕМ таласима. Макроскопска сума свих елементарних извора је нови ЕМ талас са истом фреквенцијом као и побудни али са нешто мањом таласном дужином. Дакле, до успоравања фазе долази због смањења таласне дужине ЕМ зрачења приликом проласка кроз материју, које је пак изазвано отпором који пружају електрони у материјалу принудним осцилацијама. Укупан ефекат је да се уместо првобитног ЕМ таласа чија енергија је утрошена на принудне осцилације електрона, кроз материјал простире талас исте фреквенције, али нешто мање таласне дужине. Међутим, нови микроскопски извори зрачења могу нешто енергије да емитују и у другим правцима што се експериментално испољава као распршење светлости (видети расејање светлости.
Ако су за два материјала, на датој фреквенцији, индекси преламања познати, тада се помоћу Снеловог закона може израчунати угао под којим се прелама ЕМ талас дате фреквенције при преласку из једне средине у другу.
Недавна истраживања са микроталасима су показала постојање негативног индекса преламања што се може догодити ако су и ε и μ истовремено негативни. Таква појава није очекивана у природи, али се може постићи у такозваним метаматеријалима и пружа могућност конструкције савршених сочива и других егзотичних појава попут обрнутог Снеловог закона.
Дисперзија и апсорпција
[уреди | уреди извор]У реалним материјалима до поларизације не долази истог момента када се материјал изложи пољу. Поларизација мало касни за примењеним електричним пољем што доводи до појаве диелектричних губитака. Диелектрични губици се изражавају преко комплексне пермитивности која још зависи од фреквенције. Реални материјали нису ни савршени изолатори, дакле, помало проводе једносмерну струју. Узимајући у обзир диелектричне губитке и проводљивост, може се дефинисати комплексни индекс преламања:
где се n, као и пре, односи на промену фазне брзине док κ, коефицијент екстинкције, показује меру у којој долази до апсорпционих губитака када ЕМ талас пролази кроз материјал. Обе величине, n и κ зависе од фреквенције (таласне дужине) ЕМ зрачења.
Због фреквентне зависности неопходно је навести вакуумску таласну дужину ЕМ таласа којима је индекс преламања мерен. Обично се мерења врше на неколико добро дефинисаних спектралних линија. На пример, nD је индекс преламања на Фрауенхоферовој "D" линији, центру жутог натријумовог дублета таласне дужине 589,29 nm.
Зависност индекса преламања од фреквенције (изузев у вакууму где све фреквенције имају исту брзину, c) позната је као дисперзија и захваљујући њој призма разлаже белу светлост у спектралне боје. Оптичка дисперзија је и главни извор хроматске аберације сочива. У спектралном подручју где материјал не апсорбује зрачење реални део индекса преламања расте са фреквенцијом зрачења. У близини апсорпционих максимума, међутим, зависност индекса преламања од таласне дужине поприма сложен облик и n може да опада са порастом фреквенције.
Анизотропија
[уреди | уреди извор]Индекс преламања извесних средина може да зависи од поларизације и смера кретања светлости кроз средину. Та је појава позната као двојно преламање или анизотропија и њоме се бави кристална оптика. У општем случају, диелектрична константа је тензор другог ранга (матрица 3 х 3) који не може да се опише једноставно прело индекса преламања изузев када је поларизација дуж главних оптичких оса.
У магнетно-оптичким и оптички активним материјалима, главне осе су комплексне (одговарају елиптичкој поларизацији) а диелектрични тензор је комплексни-Ермитски (за средине без губитака); за такве материјале не важи симетрија по инверзије времена и они се користе рецимо за прављење Фарадејевих изолатора.
Нелинеарност
[уреди | уреди извор]Јако електрично поље врло интензивне светлости, рецимо ласерског зрака, може да промени индекс преламања средине кроз коју пролази (нелинеарна оптика). Пораст индекса са квадратом поља (линеарна зависност индекса са интензитетом) назива се оптички Керов ефекат и доводи до појава као што су самофокусирање и само фазна модулација. Линеарна зависност индекса од јачине поља (што је могуће само у материјалима без инверзионе симетрије), назива се Покелсов ефекат.
Историја
[уреди | уреди извор]
Томас Јанг је вероватно био особа која је прва употребила и измислила назив „индекс преламања“ 1807. године.[4] Истовремено је променио ову вредност рефракционе моћи у један број, уместо традиционалног односа два броја. Однос је имао недостатак различитог изгледа. Њутн, који га је назвао „пропорција синуса инциденције и преламања“, написао га је као однос два броја, попут „529 према 396“ (или „скоро 4 према 3“; за воду).[5] Хоксби, који га је назвао „однос преламања“, написао га је као однос са фиксним бројиоцем, попут „10000 до 7451,9“ (за урин).[6] Хатон је то написао као однос са фиксним имениоцем, као што је 1,3358 према 1 (вода).[7]
Јанг није користио симбол за индекс преламања, 1807. године. У каснијим годинама, други су почели да користе различите симболе: n, m, и µ.[8][9][10] Симбол n је постепено преовладао.
Види још
[уреди | уреди извор]- Листа индекса преламања
- Селмајерова једначина
- Тотална рефлексија
- Негативни индекс преламања или Метаматеријал
- Директна метода призме
Референце
[уреди | уреди извор]- ^ а б Hecht 2002
- ^ Attwood, David (1999). Soft X-rays and extreme ultraviolet radiation: principles and applications. стр. 60. ISBN 978-0-521-02997-1.
- ^ Kinsler, Lawrence E. (2000). Fundamentals of Acoustics
 . John Wiley. стр. 136. ISBN 978-0-471-84789-2.
. John Wiley. стр. 136. ISBN 978-0-471-84789-2.
- ^ Young, Thomas (1807). A course of lectures on natural philosophy and the mechanical arts. J. Johnson. стр. 413.
- ^ Newton, Isaac (1730). Opticks: Or, A Treatise of the Reflections, Refractions, Inflections and Colours of Light. William Innys at the West-End of St. Paul's. стр. 247.
- ^ Hauksbee, Francis (1710). „A Description of the Apparatus for Making Experiments on the Refractions of Fluids”. Philosophical Transactions of the Royal Society of London. 27 (325–336): 207. S2CID 186208526. doi:10.1098/rstl.1710.0015.
- ^ Hutton, Charles (1795). Philosophical and mathematical dictionary. стр. 299. Архивирано из оригинала 2017-02-22. г.
- ^ von Fraunhofer, Joseph (1817). „Bestimmung des Brechungs und Farbenzerstreuungs Vermogens verschiedener Glasarten”. Denkschriften der Königlichen Akademie der Wissenschaften zu München. 5: 208. Архивирано из оригинала 2017-02-22. г. Exponent des Brechungsverhältnisses is index of refraction
- ^ Brewster, David (1815). „On the structure of doubly refracting crystals”. Philosophical Magazine. 45 (202): 126. doi:10.1080/14786441508638398. Архивирано из оригинала 2017-02-22. г.
- ^ Herschel, John F.W. (1828). On the Theory of Light. стр. 368. Архивирано из оригинала 2015-11-24. г.
Литература
[уреди | уреди извор]- Hecht, Eugene (2002). Optics. Addison-Wesley. ISBN 978-0-321-18878-6.
- S. Anantha Ramakrishna; Tomasz M. Grzegorczyk (2008). Physics and Applications of Negative Refractive Index Materials (PDF). CRC Press. ISBN 978-1-4200-6875-7. doi:10.1201/9781420068764.ch1. Архивирано из оригинала (PDF) 2016-03-03. г.
- Ramakrishna, S Anantha (2005). „Physics of negative refractive index materials”. Reports on Progress in Physics. 68 (2): 449. Bibcode:2005RPPh...68..449R. doi:10.1088/0034-4885/68/2/R06.
- Pendry, J.; Holden, A.; Stewart, W.; Youngs, I. (1996). „Extremely Low Frequency Plasmons in Metallic Mesostructures” (PDF). Physical Review Letters. 76 (25): 4773—4776. Bibcode:1996PhRvL..76.4773P. PMID 10061377. doi:10.1103/PhysRevLett.76.4773. Архивирано из оригинала (PDF) 2011-07-17. г. Приступљено 2011-08-18.
- Pendry, J B; Holden, A J; Robbins, D J; Stewart, W J (1998). „Low frequency plasmons in thin-wire structures” (PDF). Journal of Physics: Condensed Matter. 10 (22): 4785—4809. Bibcode:1998JPCM...10.4785P. doi:10.1088/0953-8984/10/22/007. Also see the Preprint-author's copy.
- Padilla, Willie J.; Basov, Dimitri N.; Smith, David R. (2006). „Negative refractive index metamaterials”. Materials Today. 9 (7–8): 28. doi:10.1016/S1369-7021(06)71573-5
 .
. - Slyusar V.I. Metamaterials on antenna solutions. (Free PDF download). International Conference on Antenna Theory and Techniques, 6–9 October 2009, Lviv, Ukraine.
- Bayindir, Mehmet; Aydin, K.; Ozbay, E.; Markoš, P.; Soukoulis, C. M. (2002-07-01). „Transmission properties of composite metamaterials in free space”. Applied Physics Letters. 81 (1): 120. Bibcode:2002ApPhL..81..120B. doi:10.1063/1.1492009. hdl:11693/24684
 .
.
Спољашње везе
[уреди | уреди извор]- Диелектрични материјали (на енглеском)
- NIST calculator for determining the refractive index of air
- Science World
- Filmetrics' online database Free database of refractive index and absorption coefficient information
- RefractiveIndex.INFO Refractive index database featuring online plotting and parameterisation of data
- sopra-sa.com Архивирано 2009-02-28 на сајту Wayback Machine Refractive index database as text files (sign-up required)
- LUXPOP Архивирано на веб-сајту Wayback Machine (7. септембар 2013) Thin film and bulk index of refraction and photonics calculations











