Колацова хипотеза
Изглед
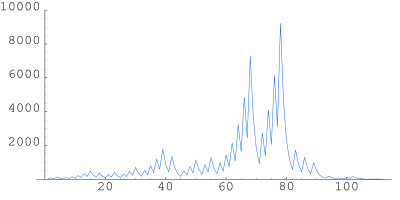
Колацова хипотеза, позната још као: 3n+1 хипотеза, хипотеза Сиракуза, Уламова хипотеза, један је од најпознатијих нерешених математичких проблема. Име је добила по немачком математичару Лотару Колацу, који је формулисао овај проблем 1. јула 1932.[1].
Формулација проблема
[уреди | уреди извор]У проблему се ради о низу целих бројева који је конструисан по следећим правилима:
- почиње се са било којим природним бројем
- ако је паран, следећи број је
- ако је непаран, следећи број је
- процес се даље понавља по горе наведеним правилима.
На пример, ако је почетни број , низ је
- 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, …
Секвенца долази до бројева 4, 2, 1 који се непрекидно понављају.
Колацова хипотеза тврди:
- Низ бројева се увек завршава секвенцом 4, 2, 1, без обзира који природан број започиње низ.
До данас, ова хипотеза није ни доказана, ни оповргнута.
Пројекат „Колацова конјектура” (енгл. Collatz Conjecture)
[уреди | уреди извор]Августа 2009. на платформи BOINC започео је пројекат рачунарске провере Колацове хипотезе[2].
До априла 2021. проверени су сви природни бројеви до 9 789 690 303 392 599 179 036[3], и сви они испуњавају услове Колацове хипотезе.
Референце
[уреди | уреди извор]- ^ P. Winkler, Mathematical Puzzles: A connoisseur’s collection (A K Peters, 2004, ISBN 978-1-56881-201-4)
- ^ Официальный сайт проекта «Collatz Conjecture» Архивирано на сајту Wayback Machine (4. децембар 2017).
- ^ „Today's High Steps”. boinc.thesonntags.com. Архивирано из оригинала 2021-04-29. г. Приступљено 2021-04-29.





