Акари (слагалица)

Овај чланак је започет или проширен кроз пројекат семинарских радова. Потребно је проверити превод, правопис и вики-синтаксу.
Када завршите са провером, допишете да након |проверено=.

Akari (Japanski: 明かり akari), такође позната и као Light up и Музеј (Japanski: 美術館 bijutsukan), је логичка слагалица коју је издао Nikoli. Akari слагалица је НП - комплетан проблем.

Историјат[уреди | уреди извор]

Прва верзија Akari слагалице је издата 2001. године. Њен оригинални креатор је јапанска издавачка кућа Nikoli, која се бави искључиво логичким слагалицама и играма. Имена која су приписана овој слагалици говоре и проблему о ком она говори: "Колики је најмањи број сијалица потребан да би се осветлиле све просторије музеја?" Због тога се табла ове слагалице може постматрати и као план интеријера неког Музеја, ради лакшег разумевања циља ове слагалице.^[1]

Правила[уреди | уреди извор]

Слагалица се састоји од квадратне мреже (табеле), састављене од белих и црних ћелија, сличне табели за укрштене речи. Потребно је поставити сијалице у беле ћелије, тако да све беле ћелије у мрежи буду осветљење, при чему ниједна сијалица не сме да обасјава другу (ниједна сијалица не сме бити у истој колони или врсти, осим уколико између њих не постоји црна ћелија). Позиције црних ћелија су унапред одређене и светлост сијалица не утиче на њих (не обасјава их). Могу да садрже бројеве од 0 до 4, који означавају број сијалица који мора да се налази уз ивице ћелије која садржи број.

Методе решавања[уреди | уреди извор]

На једноставном примеру 6x6 Akari слагалице, можемо погледати једну од метода решавања.

Уколико постоји црна ћелија са бројем 4 у себи, она може имати само једну конфигурацију за постављање сијалица, као на слици изнад, јер сијалице морају бити уз сваку ивицу те ћелије. Слично је и са црним ћелијама које садрже број 3 у себи и налазе се уз ивицу табеле или уз другу црну ћелију, или са ћелијама које садрже број 2 и налазе се у углу табеле или између друге две црне ћелије.

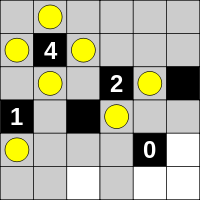
Правила о постављању сијалица нам говоре о наредним корацима решавања проблема. Због тога што светлост једне сијалице не сме да обасјава другу сијалицу, постоји само једна конфигурација решења за ћелију са бројем 1 и ћелију са бројем 2 у себи.

На самом крају примећујемо да уз ивице црне ћелије са бројем 0 у себи, не сме да стоји ниједна сијалица, одакле закључујемо да сијалица мора бити смештена у ћелију у доњем десном углу. Постављањем последње сијалице све беле ћелије табеле постају осветљене, чиме долазимо до решења Akari слагалице.

Остале методе[уреди | уреди извор]

Другачији приступ решавању Akari слагалице заснива се на проналажењу и обележавању белих ћелија (прецртавањем или уписивањем тачкице), у којима се сијалице не смеју налазити. Најбољи пример за то су ћелије суседне црној ћелији са бројем 0 у себи. Као додатни пример можемо узети конфигурацију у којој црна ћелија са бројем 1 већ има сијалицу у једној од својих суседних ћелија, из чега следи да било које друге беле ћелије, које су у њеном суседству, могу бити обележене прецртане или обележене, и у њима не може да се постави сијалица.