Бипартитне димензије

Овај чланак је започет или проширен кроз пројекат семинарских радова. Потребно је проверити превод, правопис и вики-синтаксу.
Када завршите са провером, допишете да након |проверено=.

U matematičkim oblastima teorije grafova i kombinatorne optimizacije, bipartitna dimenzija ili biklikni pokrivač broja grafa G = (V, E) је минималан број биклика (то је комплетни бипартитни подграф), који би требало да покрије све гране у E. Колекција бикликних покривача који покривају све гране у G се зове бикликни покривач грана, или понекад бикликни покривач. Бипартитна димензија у G је често означена симболом d(G).

Пример[уреди | уреди извор]

Примери бикликног покривача грана су дати у следећим дијаграмима:

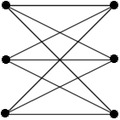
Пример за бикликну покривеност грана
Бипартитни граф...
...и покривеност са четири биклика
црвени биклик покривености
плави биклик покривености
зелени биклик покривености
црни биклик покривености

Формуле за бипартитне димензије за неки граф[уреди | уреди извор]

Бикликна димензије за комплетан граф од н чворова $K_{n}$ је $\lceil \log _{2}n\rceil$ . Бипартитна димензија крунског графа са 2н чвора једнак је $\sigma (n)$ где је

\sigma (n)=\min \left\{\,k\mid n\leq {\binom {k}{\lfloor k/2\rfloor }}\,\right\}

инверзна функција централног биномног коефицијента (de Caen, Gregory & Pullman 1981). Фишбурн и Хамер (Fishburn & Hammer 1996) су дефинисали бипартитну димензију за неке посебне графове. На пример, пут $P_{n}$ има $d(P_{n})=\lfloor n/2\rfloor$ и циклус $C_{n}$ има $d(C_{n})=\lceil n/2\rceil$ .

Израчунавање бипартитне димензије[уреди | уреди извор]

Задатак израчунавања бипартитне димензије за дати граф Г је проблем оптимизације. Проблем решавања бипартитне димензије може се формулисати као:

PRIMER: graf  $G=(V,E)$  i pozitivan ceo broj  $k$ .
PITANJE: Da li G zaista ima biklikni prekrivač grana koji sadrži najviše  $k$  biklika?

Овај проблем се јавља као проблем ГТ18 у књизи Герија и Џонсона о НП-комплетности, и доста је директна реформулација другог проблема решавања породице ограниченог скупа.

Базни проблем се појављује као проблем СП7 у књизи Герија и Џонсона. Овде, за породицу ${\mathcal {S}}=\{S_{1},\ldots ,S_{n}\}$ подскупова ограниченог скупа ${\mathcal {U}}$ , основни скуп за ${\mathcal {S}}$ је још једна породица подскупова ${\mathcal {B}}=\{B_{1},\ldots ,B_{\ell }\}$ од ${\mathcal {U}}$ тако да сваки скуп $S_{i}$ као унија неких основних елемената из ${\mathcal {B}}$ . Скуп основног проблема се сада приказује овако:

PRIMER: Ograničeni skup  ${\mathcal {U}}$ , porodica  ${\mathcal {S}}=\{S_{1},\ldots ,S_{n}\}$  podskupova  ${\mathcal {U}}$  i pozitivan ceo broj k.
PITANJE: Da li postoji osnovni skup ne veći od  $k$  za  ${\mathcal {S}}$ ?

Овај проблем је доказан да је НП-комплетан од стране Орлина (Orlin 1977), чак и за бипартитне графове. Стокмејер (Stockmeyer 1975) је раније доказао да је НП-комплетност формула основног базног проблема. Проблем остаје НП-тежак, чак и ако ограничимо нашу пажњу на бипартитне графове чија је бипартитна димензија загарантована да буде највише $O(\log \,\!n)$ , где н означава величину датог проблема (Gottlieb, Savage & Yerukhimovich 2005). Са позитивне стране, проблем је решив у полиномијалном времену на бипартитном домино-слободним графовима (Amilhastre, Janssen & Vilarem 1997).

Што се тиче постојања приближних алгоритама, Симон (Симон 1990) је доказао да проблем не може бити лепо објашњен (ако се претпостави да је '''P''' ≠ '''NP'''). Заиста, бипартитну димензију је НП-тежак приближио унутар $|V|^{1/3-\epsilon }$ за свако устаљено $\epsilon >0$ , већ за бипартитне графове (Gruber & Holzer 2007).

У супротности са тиме, доказује да је проблем прилагодљив устаљеним параметрима је вежба дизајнирања језгровитих алгоритама, како се појављује у уџбенику Даунија и Фелоуса (Downey & Fellows 1999). Флајшнер, Муџуни и Зајдер (Fleischner, Mujuni & Szeider 2009) такође су обезбедили конкретну границу величине резултујећег језгра, што је у међувремену унапредио Нор ет ал (Nor et al. 2010). Заправо, за дати бипартитни граф са н чворова, може се на време закључити да је $O(f(k))+n^{3}$ са $f(k)=2^{k2^{k-1}+3k}$ небитно да ли је његова бипартитна димензија највише к (Nor et al. 2010).

Апликације[уреди | уреди извор]

Проблем одређивања бипартитне димензије графа се појављује у разним контекстима рачунарства. На пример, у рачунарским системима, различитим корисницима система може бити дозвољен или одбијен приступ разним ресурсима. У систему за контрилу приступа] заснованог на улози, улога снабдева право приступа скупу ресурса. Корисник може да поседује вишеструке улоге и има дозволу да приступи свим ресурсима које му одобравају неке од његових улога. Такође, улога може бити у власништву више корисника. Проблем са улогама јесте наћи минимални скуп ресурса, тако да све улоге свих корисника пружају приступ свим назначеним ресурсима. Скуп корисника заједно са скупом ресурса у систему природне индукције бипартитни граф, чије гране представљају дозволе. Сваки биклик у свом графу је потенцијална улога, а оптимално решење главног проблема је управо минимални биклик покривача грана (Ene et al. 2008).

Слични сценарио се може наћи и у компјутерској безбедности, тачније у емитовању. У том случају, више порука мора бити појединачно послато комплету пријемника, преко непровереног канала. Свака порука мора да буде кодирана коришћењем неког криптографског кључа познатог само оним пријемницима којима су намењене. Сваки пријемник може имати више кључева за шифровање, а сваки кључ ће бити расподељен између више пријемника. Проблем оптималног кључа јесте пронаћи минимални скуп кључева за шифровање за обезбеђивање сигурног преноса. Као што је горе наведено, проблем се може подесити помоћу бипартитног графа чији се минимални број бикликних прекривача грана подудара са решевањем за оптимални проблем проналажења кључа (Shu, Lee & Yannakakis 2006).

Другачија апликација може се наћи у биологији, где се минимални број бикликних покривености грана користи у математичким обрасцима леукоцитног антигена код људи (ХЛА) (Nau et al. 1978).

Референце[уреди | уреди извор]

Литература[уреди | уреди извор]

Амилхастре, Јéрôме; Јанссен, Пхилиппе; Виларем, Марие-Цатхерине (1997), „Цомпутинг а минимум бицлиqуе цовер ис полyномиал фор бипартите домино-фрее грапхс”, Процеедингс оф тхе Еигхтх Аннуал АЦМ-СИАМ Сyмпосиум он Дисцрете Алгоритхмс, 5–7 Јануарy 1997, Неw Орлеанс, Лоуисиана., АЦМ/СИАМ, стр. 36—42
де Цаен, Доминиqуе; Грегорy, Давид А.; Пуллман, Норман Ј. (1981), „Тхе Боолеан ранк оф зеро-оне матрицес”, Ур.: Цадоган, Цхарлес C., 3рд Цариббеан Цонференце он Цомбинаторицс анд Цомпутинг, Департмент оф Матхематицс, Университy оф тхе Wест Индиес, стр. 169—173 .
Доwнеy, Род; Феллоwс, Мицхаел Р. (1999), Параметеризед цомплеxитy, Спрингер, ИСБН 978-0-387-94883-6 .
Ене, Алина; Хорне, Wиллиам Г.; Милосављевиц, Никола; Рао, Прасад; Сцхреибер, Роберт; Тарјан, Роберт Ендре (2008), „Фаст еxацт анд хеуристиц метходс фор роле минимизатион проблемс”, Ур.: Раy, Индраксхи; Ли, Нингхуи, 13тх АЦМ Сyмпосиум он Аццесс Цонтрол Моделс анд Тецхнологиес (САЦМАТ 2008), АЦМ, стр. 1—10 .
Фисхбурн, Петер C.; Хаммер, Петер L. (1996), „Бипартите дименсионс анд бипартите дегреес оф грапхс”, Дисцрете Матхематицс, 160 (1–3): 127—148, дои:10.1016/0012-365X(95)00154-О .
Флеисцхнер, Херберт; Мујуни, Егберт; Паулусма, Даниëл; Сзеидер, Стефан (2009), „Цоверинг грапхс wитх феw цомплете бипартите субграпхс”, Тхеоретицал Цомпутер Сциенце, 410 (21-23): 2045—2053, дои:10.1016/ј.тцс.2008.12.059 .
Гареy, Мицхаел Р.; Јохнсон, Давид С. (1979), Цомпутерс анд Интрацтабилитy: А Гуиде то тхе Тхеорy оф НП-Цомплетенесс, W.Х. Фрееман, ИСБН 978-0-7167-1045-5 .
Готтлиеб, Лее-Ад Ј.; Саваге, Јохн Е.; Yерукхимовицх, Аркадy (2005), „Еффициент дата стораге ин ларге наноарраyс”, Тхеорy оф Цомпутинг Сyстемс, 38 (4): 503—536, дои:10.1007/с00224-004-1196-9 .
Грубер, Херманн; Холзер, Маркус (2007), „Инаппроxимабилитy оф Нондетерминистиц Стате анд Транситион Цомплеxитy Ассуминг П <> НП.”, Ур.: Харју, Терјо; Кархумäки, Јухани; Лепистö, Арто, 11тх Интернатионал Цонференце он Девелопментс ин Лангуаге Тхеорy (ДЛТ 2007), ЛНЦС, 4588, Турку, Финланд: Спрингер, стр. 205—216, дои:10.1007/978-3-540-73208-2_21 .
Монсон, Сyлвиа D.; Пуллман, Норман Ј.; Реес, Ролф (1995), „А сурвеy оф цлиqуе анд бицлиqуе цоверингс анд фацторизатионс оф (0,1)-матрицес”, Буллетин оф тхе ИЦА, 14: 17—86 .
D. С. Нау, D. С.; Маркоwскy, Г.; Wоодбурy, M. А.; Амос, D. Б. (1978), „А матхематицал аналyсис оф хуман леукоцyте антиген серологy” (ПДФ), Матхематицал Биосциенцес, 40: 243—270, дои:10.1016/0025-5564(78)90088-3 .
Нор, Игор; Хермелин, Даннy; Цхарлат, Сyлваин; Енгелстадтер, Јан; Реутер, Маx; Дурон, Оливиер; Сагот, Марие-Франце (2010). „Мод/Ресц Парсимонy Инференце”. арXив:1002.1292  [цс.ДС].
Орлин, Јамес (1977), „Цонтентмент ин грапх тхеорy: цоверинг грапхс wитх цлиqуес”, Индагатионес Матхематицае, 80 (5): 406—424, дои:10.1016/1385-7258(77)90055-5 .
Сху, Гуоqианг; Лее, Давид; Yаннакакис, Михалис (2006), „А ноте он броадцаст енцрyптион кеy манагемент wитх апплицатионс то ларге сцале емергенцy алерт сyстемс.”, 20тх Интернатионал Параллел анд Дистрибутед Процессинг Сyмпосиум (ИПДПС 2006), ИЕЕЕ .
Симон, Ханс-Улрицх (1990), „Он Аппроxимате Солутионс фор Цомбинаториал Оптимизатион Проблемс”, СИАМ Јоурнал он Дисцрете Матхематицс, 3 (2): 294—310, дои:10.1137/0403025 .
Стоцкмеyер, Ларрy Ј. (1975), Тхе сет басис проблем ис НП-цомплете, Тецхницал Репорт РЦ-5431, ИБМ .

Спољашње везе[уреди | уреди извор]

blog entry about bipartite dimension by David Eppstein