Центрипетална сила

На тело које се креће по кружници делује центрипетална сила која је усмерена дуж полупречника круга тачки на кружници у којој се тело у том тренутку налази ка центру кружнице.

Центрипетална сила (од латинских речи centrum, „центар” и petere, „тражити”) је сила која узрокује да тело следи закривљену путању. Њен правац је увек ортогоналан на вектор брзине тела у датој тачки и усмерен је према центру закривљености путање.

Најједноставнији случај деловања центрипеталне силе је кружно кретање у којем се тело креће константном брзином по кружници. Центрипетална сила је у овом случају усмерена дуж полупречника круга од тачке у којој се тело у датом тренутку налази ка центру круга.

Математички опис кретања тела по кружној путањи извео је холандски физичар Кристијан Хајгенс 1659. године. Исак Њутн је центрипеталну силу описао као „силу којом се тела повлаче или присиљавају, или на било који начин теже ка тачки као центру”. У Њутновој механици, сила гравитација је центрипетална сила која је одговорна за орбитална кретања планета, сателита, итд.

Сноп електрона закривљен магнетним пољем које у овом случају има улогу центрипеталне силе. Електрони се налазе у посуди испуњеној гасом и у судару са молекулима гаса емитује се светлост љубичасте боје, тако да она оцртава трајекторију кретања електрона.

Појам центрифугалне силе се објашњава преко центрипеталне силе. Центрипетална сила је реална сила која делује на тело при кружном кретању гледано из стационарног инерцијалног система референције. У покретном неинерцијалном систему референције везаном за тело које ротира, не види се центрипетална сила, али да би се објаснило кретање тела уводи се центрифугална сила која има исти интензитет и правац као центрипетална сила, али је супротног смера у односу на центрипеталну силу и усмерена је од центра закривљене путање ка телу.

Формула

Центрипетална сила која делује на објект масе m који се креће по кружници је задата Другим Њутновим законом:

$F_{c}=ma_{c}$

где је $a_{c}$ центрипетално убрзање које се за тело које се креће тангенцијалном брзином v дуж пута радијуса закривљености r може израчунати као:

$a_{c}={\frac {v}{t}}{\hat {r}}={\frac {r\omega }{t}}{\hat {r}}=v\omega ={\frac {v^{2}}{r}}$

тако да за центрипеталну силу важи:

$F_{c}=ma_{c}={\frac {mv^{2}}{r}}$

$$a_{c}=\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {v}}|}{\Delta t}}$$

где је $\Delta {\textbf {v}}$ разлика између вектора брзине. Пошто вектори брзине у горњем дијаграму имају константну величину и пошто је сваки окомит на свој одговарајући вектор положаја, једноставно одузимање вектора подразумева два слична једнакокрака троугла са конгруентним угловима – један који садржи основу од $\Delta {\textbf {v}}$ и дужину ноге од $v$, а други основу од $\Delta {\textbf {r}}$ (разлика у вектору положаја) и дужина ноге од $r$:

$${\frac {|\Delta {\textbf {v}}|}{v}}={\frac {|\Delta {\textbf {r}}|}{r}}$$

$$|\Delta {\textbf {v}}|={\frac {v}{r}}|\Delta {\textbf {r}}|$$

Стога, $|\Delta {\textbf {v}}|$ може се заменити са ${\frac {v}{r}}|\Delta {\textbf {r}}|$:

$$a_{c}=\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {v}}|}{\Delta t}}={\frac {v}{r}}\lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta t}}=\omega \lim _{\Delta t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta t}}=v\omega ={\frac {v^{2}}{r}}$$

правац силе је ка центру кружнице у којој се објекат креће, односно оскулирајућим кругом (круг који најбоље одговара локалној путу, ако путања није кружна). Брзина у формули је на квадрат, тако да је за двоструку брзину потребна четири пута већа сила. Инверзни однос са радијусом кривине показује да је за пола радијалног раста потребна двоструко већа сила.

Центрипетална сила изражена преко угаоних величина

Центрипетална сила се понекад изражава преко угаоне брзине објекта ω који ротира око центра круга. Угаона брзина је везана за тангенцијалну брзину формулом

$v=\omega r$

тако да је центрипетална сила преко угаоне брзине изражена као:

$F_{c}=mr\omega ^{2}\,.$

Центрипетална сила се за периодична кретања може изразити и преко периода T , односно времена потребном да тело направи пун обрт око центра круга. Како је веза између угаоне брзине и периода $\omega ={\frac {2\pi }{T}}\,$, једначина за центрипеталну силу постаје:

$F_{c}=mr\left({\frac {2\pi }{T}}\right)^{2}.$

Центрипетална сила код релативистичког кретања

У акцелераторима честица, брзина честица може бити веома висока (упоредива са брзином светлости у вакууму). За кретање код тако великих релативистичких брзина не важи класична механика, већ се мора користити физика специјалне релативности.

Израз за центрипеталну силу при релативистичком кретању је:

$F_{c}={\frac {\gamma mv^{2}}{r}}=\gamma mv\omega$

где је

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

Лоренцов фактор.

Извори

Тело које има равномерно кружно кретање захтева центрипеталну силу, према оси као што је приказано, да задржи своју кружну путању.

У случају предмета који се љуља око краја ужета у хоризонталној равни, центрипетална сила на предмет се обезбеђује затезањем ужета. Пример ужета је пример који укључује силу 'повлачења'. Центрипетална сила се такође може испоручити као сила 'гурања', као на пример у случају када нормална реакција зида обезбеђује центрипеталну силу за зид смрти или возача ротора.

Њутнова идеја о центрипеталној сили одговара ономе што се данас назива централном силом. Када је сателит у орбити око планете, гравитација се сматра центрипеталном силом иако је у случају ексцентричних орбита гравитациона сила усмерена ка фокусу, а не према тренутном центру закривљености.

Други пример центрипеталне силе настаје у спирали која се налази када се наелектрисана честица креће у униформном магнетном пољу у одсуству других спољних сила. У овом случају, магнетна сила је центрипетална сила која делује према оси спирале.

Примери

За тело које помоћу ужета ротира у хоризонталној равни, у улози центрипеталне силе која изазива кружно кретање тела је сила затезања ужета. У овом случају центрипетална сила је сила повлачења. Центрипетална сила може бити пружена и као сила гурања, као у случају када нормална реакција зида пружа центрипеталну силу возачу на зиду смрти.

Када наелектрисана честица уђе у униформно магнетно поље под правим углом у односу на правац поља, магнетна сила ће бити центрипетална сила за наелектрисану честицу и у одсуству других спољашњих сила, честица ће се кретати по спирали око магнетног поља. Када наелектрисана честица изгуби своју брзину, кретаће се по кружници око осе магнетног поља.

Анализа неколико случајева

Испод су дата три примера све веће сложености, са извођењем формула за брзину и убрзање.

Уједначено кружно кретање

Такође погледајте: Равномерно кружно кретање

Равномерно кружно кретање се односи на случај константне брзине ротације. Следе два приступа описа овог случаја.

Рачунско извођење

У две димензије, вектор положаја ${\textbf {r}}$, који има величину (дужину) $r$ и усмерен под углом $\theta$ изнад x-осе, може се изразити у Декартовим координатама помоћу јединичних вектора ${\hat {\mathbf {x} }}$ анд ${\hat {\mathbf {y} }}$: $${\textbf {r}}=r\cos(\theta ){\hat {\mathbf {x} }}+r\sin(\theta ){\hat {\mathbf {y} }}.$$

Претпоставка о равномерном кружном кретању захтева три услова:

• Објекат се креће само по кругу.
• Полупречник круга $r$ се не мења током времена.
• Објекат се креће константном угаоном брзином $\omega$ око круга. Према томе, $\theta =\omega t$ где је $t$ време.

Брзина ${\textbf {v}}$ кретања и убрзање ${\textbf {a}}$ су први и други деривати положаја у односу на време:

$${\textbf {r}}=r\cos(\omega t){\hat {\mathbf {x} }}+r\sin(\omega t){\hat {\mathbf {y} }},$$ $${\textbf {v}}={\dot {\textbf {r}}}=-r\omega \sin(\omega t){\hat {\mathbf {x} }}+r\omega \cos(\omega t){\hat {\mathbf {y} }},$$ $${\textbf {a}}={\ddot {\textbf {r}}}=-\omega ^{2}(r\cos(\omega t){\hat {\mathbf {x} }}+r\sin(\omega t){\hat {\mathbf {y} }}).$$

Термин у загради је оригинални израз ${\textbf {r}}$ у Декартовим координатама. Следствено, $${\textbf {a}}=-\omega ^{2}{\textbf {r}}.$$ негативна вредност показује да је убрзање усмерено ка центру круга (насупрот полупречника), те се зато назива „центрипетално” (тј. „тражећи центар”). Док објекти природно прате праву путању (због инерције), ово центрипетално убрзање описује кружну путању кретања узроковану центрипеталном силом.

Извођење помоћу вектора

Векторски односи за равномерно кружно кретање; вектор Ω који представља ротацију је нормалан на раван орбите са поларитетом одређеним правилом десне руке и магнитудом дθ /дт.

Слика десно приказује векторске односе за равномерно кружно кретање. Сама ротација је представљена вектором угаоне брзине Ω, који је нормалан на раван орбите (помоћу правила десне руке) и има величину дату као:

$|\mathbf {\Omega } |={\frac {\mathrm {d} \theta }{\mathrm {d} t}}=\omega \ ,$

са θ угаоним положајем у тренутку т. У овом пододељку, дθ/дт се претпоставља да је константно, независно од времена. Пређено растојање дℓ честице за време дт дуж кружне путање је

$\mathrm {d} {\boldsymbol {\ell }}=\mathbf {\Omega } \times \mathbf {r} (t)\mathrm {d} t\ ,$

које по својствима векторског унакрсног производа има магнитуду рдθ и налази се у правцу тангенте на кружну путању.

Сходно томе,

${\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\lim _{{\Delta }t\to 0}{\frac {\mathbf {r} (t+{\Delta }t)-\mathbf {r} (t)}{{\Delta }t}}={\frac {\mathrm {d} {\boldsymbol {\ell }}}{\mathrm {d} t}}\ .$

Другим речима,

$\mathbf {v} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\frac {\mathrm {d} \mathbf {\boldsymbol {\ell }} }{\mathrm {d} t}}=\mathbf {\Omega } \times \mathbf {r} (t)\ .$

Диференцирајући у односу на време, $$\mathbf {a} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {v} }{d\mathrm {t} }}=\mathbf {\Omega } \times {\frac {\mathrm {d} \mathbf {r} (t)}{\mathrm {d} t}}=\mathbf {\Omega } \times \left[\mathbf {\Omega } \times \mathbf {r} (t)\right]\ .$$

Лагранжова формула наводи: $$\mathbf {a} \times \left(\mathbf {b} \times \mathbf {c} \right)=\mathbf {b} \left(\mathbf {a} \cdot \mathbf {c} \right)-\mathbf {c} \left(\mathbf {a} \cdot \mathbf {b} \right)\ .$$

Примењујући Лагранжову формулу уз запажање да је Ω • р(т) = 0 у сваком тренутку, $$\mathbf {a} =-{|\mathbf {\Omega |} }^{2}\mathbf {r} (t)\ .$$

Речју, убрзање је усмерено директно супротно од радијалног померања р у сваком тренутку и има магнитуду: $$|\mathbf {a} |=|\mathbf {r} (t)|\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}=r{\omega }^{2}$$

где вертикалне шипке |...| означавају векторску величину, која је у случају р(т) једноставно полупречник р путање. Овај резултат се слаже са претходним одељком, иако је нотација мало другачија.

Када се брзина ротације учини константном у анализи неуједначеног кружног кретања, та анализа се слаже са овом.

Предност векторског приступа је у томе што је очигледно независан од било ког координатног система.

Пример: Нагнуто скретање

Главни чланак: Нагнуто скретање

Такође погледајте: Реактивна центрифугална сила

Горњи панел: Лопта на нагнутој кружној стази која се креће константном брзином в; Доњи панел: Силе на лопти

Горњи панел на слици десно приказује лопту у кружном кретању на нагнутој кривини. Крива је нагнута под углом θ у односу на хоризонталу, а површина пута се сматра клизавом. Циљ је пронаћи који угао мора имати банкина да лопта не склизне са пута. Интуиција нам говори да ће, на равној кривини без икаквог нагиба, лопта једноставно склизнути са пута; док са веома стрмим нагибом, лопта ће клизити до центра осим ако брзо путује кривином.

Осим било каквог убрзања које се може догодити у правцу путање, доњи панел горње слике показује силе на лопту. Постоје две силе; једна је сила гравитације вертикално надоле кроз центар масе лопте мг, где је м маса лопте, а г гравитационо убрзање; друга је нормална сила навише коју врши пут под правим углом у односу на површину пута ма_н. Центрипетална сила коју захтева закривљено кретање је такође приказана изнад. Ова центрипетална сила није трећа сила примењена на лопту, већ се мора обезбедити нето силом на лопту која је резултат векторског сабирања нормалне силе и силе гравитације. Резултантна или нето сила на лопти пронађена векторским сабирањем нормалне силе коју врши пут и вертикалне силе услед гравитације мора бити једнака центрипеталној сили коју диктира потреба да се путује кружном путањом. Закривљено кретање се одржава све док ова нето сила обезбеђује центрипеталну силу потребну за кретање.

Хоризонтална нето сила на лопту је хоризонтална компонента силе од пута, која има магнитуду |Ф_х| = м|а_н| син θ. Вертикална компонента силе од пута мора да се супротстави гравитационој сили: |Ф_в| = м|а_н| цос θ = м|г|, што имплицира |а_н| = |г| / цос θ. Замена у горњу формулу за |Ф_х| даје хоризонталну силу која је: $$|\mathbf {F} _{\mathrm {h} }|=m|\mathbf {g} |{\frac {\sin \theta }{\cos \theta }}=m|\mathbf {g} |\tan \theta \,.$$

С друге стране, при брзини |в| на кружној путањи полупречника р, кинематика каже да је сила потребна да се лопта непрекидно окреће у заокрету радијално унутра центрипетална сила Ф_ц магнитуде: $$|\mathbf {F} _{\mathrm {c} }|=m|\mathbf {a} _{\mathrm {c} }|={\frac {m|\mathbf {v} |^{2}}{r}}\,.$$

Следствено, лопта је на стабилној путањи када је угао пута постављен тако да се задовољи услов: $$m|\mathbf {g} |\tan \theta ={\frac {m|\mathbf {v} |^{2}}{r}}\,,$$ или, $$\tan \theta ={\frac {|\mathbf {v} |^{2}}{|\mathbf {g} |r}}\,.$$

Како се угао нагиба θ приближава 90°, тангентна функција се приближава бесконачности, дозвољавајући веће вредности за |в|²/р. Ова једначина наводи да за веће брзине (веће |в|) пут мора бити стрмије нагнут (већа вредност за θ), а за оштрија скретања (мање р) пут такође мора бити стрмије нагнут, што је у складу са интуицијом. Када угао θ не задовољава горњи услов, хоризонтална компонента силе коју врши пут не обезбеђује исправну центрипеталну силу, а додатна сила трења тангенцијална на површину пута се позива да обезбеди разлику. Ако трење то не може да уради (тј. коефицијент трења је прекорачен), лопта клизи на други радијус где се равнотежа може остварити.

Ове идеје важе и за ваздушни лет. Погледајте упутство за ФАА пилоте.

Неуједначено кружно кретање

Види још: Кружно кретање и Неуједначено кружно кретање

Брзина и убрзање за неуједначено кружно кретање: вектор брзине је тангенцијалан на орбиту, али вектор убрзања није радијално унутра због своје тангенцијалне компоненте а_θ која повећава брзину ротације: дω / дт = а_θ / Р.

Као генерализација случаја равномерног кружног кретања, претпоставимо да угаона брзина ротације није константна. Убрзање сада има тангенцијалну компоненту, као што је приказано на слици десно. Овај случај се користи за демонстрирање стратегије деривације засноване на поларном координатном систему.

Нека је р(т) вектор који описује положај тачке масе као функцију времена. Пошто се претпоставља кружно кретање, нека је р(т) = Р·у_р, где је Р константа (полупречник круга), а у_р је јединични вектор који иде од координатног почетка до тачке масе. Правац у_р је описан са θ, углом између x-осе и јединичног вектора, мерено у смеру супротном од казаљке на сату од x-осе. Други јединични вектор за поларне координате, у_θ је окомит на у_р и усмерен је у правцу повећања θ. Ови поларни јединични вектори могу се изразити у виду Декартових јединичних вектора у x и y правцима, означени као ${\hat {\mathbf {i} }}$ и ${\hat {\mathbf {j} }}$, респективно: $$\mathbf {u} _{r}=\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}$$ анд $$\mathbf {u} _{\theta }=-\sin \theta \ {\hat {\mathbf {i} }}+\cos \theta \ {\hat {\mathbf {j} }}.$$

Може се диференцирати да би се пронашла брзина: $${\begin{aligned}\mathbf {v} &=r{\frac {d\mathbf {u} _{r}}{dt}}\\&=r{\frac {d}{dt}}\left(\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}{\frac {d}{d\theta }}\left(\cos \theta \ {\hat {\mathbf {i} }}+\sin \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}\left(-\sin \theta \ {\hat {\mathbf {i} }}+\cos \theta \ {\hat {\mathbf {j} }}\right)\\&=r{\frac {d\theta }{dt}}\mathbf {u} _{\theta }\\&=\omega r\mathbf {u} _{\theta }\end{aligned}}$$ где је ω угаона брзина дθ/дт.

Овај резултат за брзину одговара очекивањима да брзина треба да буде усмерена тангенцијално на круг и да величина брзине треба да буде рω. Поновним диференцирањем и констатацијом да $${\frac {d\mathbf {u} _{\theta }}{dt}}=-{\frac {d\theta }{dt}}\mathbf {u} _{r}=-\omega \mathbf {u} _{r}\ ,$$ налази се да је убрзање а: $$\mathbf {a} =r\left({\frac {d\omega }{dt}}\mathbf {u} _{\theta }-\omega ^{2}\mathbf {u} _{r}\right)\ .$$

Дакле, радијалне и тангенцијалне компоненте убрзања су: $$\mathbf {a} _{r}=-\omega ^{2}r\ \mathbf {u} _{r}=-{\frac {|\mathbf {v} |^{2}}{r}}\ \mathbf {u} _{r}$$ анд $$\mathbf {a} _{\theta }=r\ {\frac {d\omega }{dt}}\ \mathbf {u} _{\theta }={\frac {d|\mathbf {v} |}{dt}}\ \mathbf {u} _{\theta }\ ,$$ где је |в| = р ω магнитуда брзине.

Ове једначине математички изражавају да се, у случају објекта који се креће дуж кружне путање са променљивом брзином, убрзање тела може разложити на окомиту компоненту која мења смер кретања (центрипетално убрзање) и паралелу, или тангенцијална компонента, која мења брзину.

Генерално планарно кретање

Види још: Генерализоване силе, Генерализована сила, Криволинијске координате, Генерализоване координате и Ортогоналне координате

Вектор положаја р, увек усмерен радијално од координатног почетка

Вектор брзине в, увек тангентан на путању кретања.

Вектор убрзања а, није паралелан са радијалним кретањем, већ је померен угаоним и Кориолисовим убрзањем, нити је тангентан на путању, већ је померен центрипеталним и радијалним убрзањима.

Кинематички вектори у равним поларним координатама. Обратите пажњу да подешавање није ограничено на 2д простор, већ на раван у било којој вишој димензији.

Поларни јединични вектори у два времена т и т + дт за честицу са путањом р ( т ); са леве стране јединични вектори у_ρ и у_θ у два времена се померају тако да им се сви репови састају, и приказано је да прате лук круга јединичног полупречника. Њихова ротација у времену дт је дθ, под истим углом као и ротација путање р ( т ).

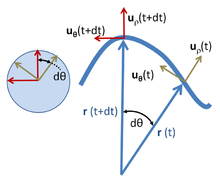
Поларне координате

Горе наведени резултати могу се можда једноставније извести у поларним координатама, и истовремено проширити на опште кретање унутар равни, као што је приказано у наставку. Поларне координате у равни користе радијални јединични вектор у_ρ и угаони јединични вектор у_θ, као што је приказано изнад. Честица на позицији р је описана са:

$$\mathbf {r} =\rho \mathbf {u} _{\rho }\ ,$$

где се ознака ρ користи да опише растојање путање од координатног почетка уместо Р да би се нагласило да ово растојање није фиксно, већ да варира са временом. Јединични вектор у_ρ путује са честицом и увек је усмерен у истом правцу као р(т). Јединични вектор у_θ такође путује са честицом и остаје ортогоналан на у_ρ. Дакле, у_ρ и у_θ формирају локални Декартов координатни систем везан за честицу и везан за путању коју је прешла честица. Померањем јединичних вектора тако да им се репови поклапају, као што се види у кругу лево на слици изнад, види се да у_ρ и у_θ формирају пар под правим углом са врховима на јединичном кругу који се крећу напред-назад по ободу овог круга са истим углом θ(т) као р(т).

Када се честица креће, њена брзина је

$\mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho {\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}\,.$

За процену брзине потребан је извод јединичног вектора у_ρ. Пошто је у_ρ јединични вектор, његова величина је фиксна и може се мењати само у правац, односно његова промена ду_ρ има компоненту само управну на у_ρ. Када трајекторија р(т) ротира за износ дθ, у_ρ, који је усмерен у истом правцу као и р(т), он такође ротира за дθ. Види слику изнад. Према томе, промена у_ρ је

$\mathrm {d} \mathbf {u} _{\rho }=\mathbf {u} _{\theta }\mathrm {d} \theta \,,$

или

${\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}=\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\,.$

На сличан начин је проналази брзина промене у_θ. Као и код у_ρ, у_θ је јединични вектор и може само да се ротира без промене величине. Да остане ортогоналан на у_ρ док трајекторија р(т) ротира за износ дθ, у_θ, који је ортогоналан на р(т), такође ротира за дθ. Види слику изнад. Према томе, промена ду_θ је ортогонална на у_θ и пропорционална са дθ (погледајте слику изнад):

${\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}=-{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {u} _{\rho }\,.$

Једначина изнад показује да је предзнак негативан: да би се одржала ортогоналност, ако је ду_ρ позитиван са дθ, онда ду_θ мора да се смањи.

Замена деривата у_ρ у израз за брзину:

$\mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}=v_{\rho }\mathbf {u} _{\rho }+v_{\theta }\mathbf {u} _{\theta }=\mathbf {v} _{\rho }+\mathbf {v} _{\theta }\,.$

Да би се добило убрзање, врши се још једно временска диференцијација:

$\mathbf {a} ={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\,.$

Заменом деривата од у_ρ и у_θ, убрзање честице је:

${\begin{aligned}\mathbf {a} &={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}-\rho \mathbf {u} _{\rho }\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\ ,\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]\\&=\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} v_{\rho }}{\mathrm {d} t}}-{\frac {v_{\theta }^{2}}{\rho }}\right]+\mathbf {u} _{\theta }\left[{\frac {2}{\rho }}v_{\rho }v_{\theta }+\rho {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {v_{\theta }}{\rho }}\right]\,.\end{aligned}}$

Као посебан пример, ако се честица креће у кругу константног радијуса Р, онда је дρ/дт = 0, в = в_θ, и:

$$\mathbf {a} =\mathbf {u} _{\rho }\left[-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]=\mathbf {u} _{\rho }\left[-{\frac {v^{2}}{r}}\right]+\mathbf {u} _{\theta }\left[{\frac {\mathrm {d} v}{\mathrm {d} t}}\right]\$$

где је $v=v_{\theta }.$

Ови резултати се слажу са онима изнад за неуједначено кружно кретање. Погледајте и чланак о неуједначеном кружном кретању. Ако се ово убрзање помножи са масом честице, водећи члан је центрипетална сила, а негативна вредност другог члана који се односи на угаоно убрзање се понекад назива Ојлерова сила.

За путање које нису кружно кретање, на пример, општију путању приказану на горњој слици, тренутни центар ротације и полупречник кривине путање су повезани само индиректно са координатним системом дефинисаним са у_ρ и у_θ и са дужином |р(т)| = ρ. Сходно томе, у општем случају, није једноставно одвојити центрипеталне и Ојлерове чланове из горње опште једначине убрзања. Да би се директно адресирало ово питање, пожељније су локалне координате, као што ће бити речи у наставку.

Локалне координате

Локални координатни систем за планарно кретање на кривој. Два различита положаја су приказана за растојања с и с + дс дуж криве. На свакој позицији с, јединични вектор у_н је усмерен дуж спољашње нормале на криву, а јединични вектор у_т је тангенцијалан на путању. Полупречник кривине путање је ρ као што је пронађено из брзине ротације тангенте на криву у односу на дужину лука, а представља полупречник оскулационог круга на позицији с. Јединични круг са леве стране показује ротацију јединичних вектора са с.

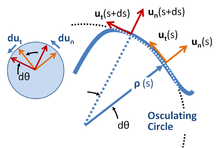
Локалне координате означавају скуп координата које путују са честицом, и имају оријентацију која је одређена путањом честице. Јединични вектори се формирају као што је приказано на слици десно, оба, тангенцијални и нормални на путању. Овај координатни систем се понекад назива унутрашњим координатама или координатама путање или нт-координатама, за нормално-тангенцијално, које се односе на ове јединичне векторе. Ове координате су веома посебан пример општијег концепта локалних координата из теорије диференцијалних облика.

Растојање дуж путање честице је дужина лука с, за коју се сматра да је позната функција времена.

$s=s(t)\ .$

Центар закривљености је дефинисан на свакој позицији с која се налази на растојању ρ (полупречник кривине) од криве на линији дуж нормале у_н (с). Захтевано растојање ρ(с) на дужини лука с је дефинисано у смислу брзине ротације тангенте на криву, која је заузврат одређена самом путањом. Ако је оријентација тангенте у односу на неку почетну позицију θ(с), онда је ρ(с) дефинисано изводом дθ/дс:

${\frac {1}{\rho (s)}}=\kappa (s)={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .$

Полупречник криве се обично узима да је позитиван (односно као апсолутна вредност), док је закривљеност κ величина са предзнаком.

Геометријски приступ проналажењу центра кривине и полупречника кривине користи ограничавајући процес који води до оскулационог круга. Види слику изнад.

Користећи ове координате, кретање дуж путање се посматра као низ кружних путања стално променљивог центра, и на свакој позицији с представља неуједначено кружно кретање на тој позицији полупречника ρ. Локална вредност угаоне брзине ротације је тада дата са:

$\omega (s)={\frac {\mathrm {d} \theta }{\mathrm {d} t}}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}{\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {1}{\rho (s)}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {v(s)}{\rho (s)}}\ ,$

са локалном брзином в датом са:

$v(s)={\frac {\mathrm {d} s}{\mathrm {d} t}}\ .$

Што се тиче осталих примера изнад, пошто јединични вектори не могу да мењају величину, њихова брзина промене је увек окомита на њихов правац (погледајте леви уметак на слици изнад):

${\frac {d\mathbf {u} _{\mathrm {n} }(s)}{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {d\theta }{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {1}{\rho }}\ ;$ ${\frac {d\mathbf {u} _{\mathrm {t} }(s)}{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} \theta }{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {1}{\rho }}\ .$

Према томе, брзина и убрзање су:

$\mathbf {v} (t)=v\mathbf {u} _{\mathrm {t} }(s)\ ;$

и користећи ланчано правило диференцијације:

$\mathbf {a} (t)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\ ;$ wитх тхе тангентиал аццелератион ${\frac {\mathrm {\mathrm {d} } v}{\mathrm {\mathrm {d} } t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ v\ .$

У овом локалном координатном систему, убрзање личи на израз за неуједначено кружно кретање са локалним радијусом ρ(с), а центрипетално убрзање је идентификовано као други члан.

Проширивање овог приступа на тродимензионалне просторне криве доводи до Френет-Серетових формула.

Алтернативни приступ

Гледајући горњу слику, неко би се могао запитати да ли је узета у обзир разлика у кривини између ρ(с) и ρ(с + дс) при израчунавању дужине лука као дс = ρ(с)дθ. Уверење по овом питању може се наћи коришћењем формалнијег приступа који је наведен у наставку. Овај приступ успоставља везу и са чланком о закривљености.

Да би се увели јединични вектори локалног координатног система, један приступ је да се почне од Декартових координата и опишу локалне координате у смислу ових Декартових координата. У погледу дужине лука с, нека путања буде описана као: $$\mathbf {r} (s)=\left[x(s),\ y(s)\right].$$

Тада се инкрементално померање дуж путање дс описује са: $$\mathrm {d} \mathbf {r} (s)=\left[\mathrm {d} x(s),\ \mathrm {d} y(s)\right]=\left[x'(s),\ y'(s)\right]\mathrm {d} s\ ,$$

где се уводе прости бројеви за означавање извода у односу на с. Величина овог помака је дс, што показује да:

$\left[x'(s)^{2}+y'(s)^{2}\right]=1\ .$ (Еq. 1)

Ово померање је нужно тангента на криву у с, показујући да је јединични вектор тангента на криву:

$$\mathbf {u} _{\mathrm {t} }(s)=\left[x'(s),\ y'(s)\right],$$

док је спољашњи јединични вектор нормалан на криву

$$\mathbf {u} _{\mathrm {n} }(s)=\left[y'(s),\ -x'(s)\right],$$

Ортогоналност се може проверити показујући да је скаларни производ вектор нула. Јединична величина ових вектора је последица једначине 1. Користећи вектор тангенте, угао θ тангенте на криву је дат са:

$$\sin \theta ={\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=y'(s)\ ;$$ анд $\cos \theta ={\frac {x'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=x'(s)\ .$

Полупречник кривине се уводи потпуно формално (без потребе за геометријском интерпретацијом) као:

$${\frac {1}{\rho }}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .$$

Извод на θ се може наћи из оног за синθ: $${\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}=\cos \theta {\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}\cos \theta \ ={\frac {1}{\rho }}x'(s)\ .$$

Сада: $${\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}={\frac {\mathrm {d} }{\mathrm {d} s}}{\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}={\frac {y''(s)x'(s)^{2}-y'(s)x'(s)x''(s)}{\left(x'(s)^{2}+y'(s)^{2}\right)^{3/2}}}\ ,$$

у коме је именилац јединица. Са овом формулом за извод синуса, полупречник кривине постаје:

$${\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}=y''(s)x'(s)-y'(s)x''(s)={\frac {y''(s)}{x'(s)}}=-{\frac {x''(s)}{y'(s)}}\ ,$$

где еквиваленција облика произилази из диференцијације једначине 1:

$$x'(s)x''(s)+y'(s)y''(s)=0\ .$$

Са овим резултатима, убрзање се може наћи да је:

$${\begin{aligned}\mathbf {a} (s)&={\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {v} (s)={\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\frac {\mathrm {d} s}{\mathrm {d} t}}\left(x'(s),\ y'(s)\right)\right]\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)+\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}\left(x''(s),\ y''(s)\right)\\&=\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)-\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}{\frac {1}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\end{aligned}}$$

што се може проверити узимањем скаларног производа са јединичним векторима у_т(с) и у_н(с). Овај резултат за убрзање је исти као и за кружно кретање засновано на полупречнику ρ. Користећи овај координатни систем у инерцијалном оквиру, лако је идентификовати силу која је нормална на путању као центрипеталну силу, а ону паралелну са путањом као тангенцијалну силу. Са квалитативног становишта, путања се може апроксимирати луком кружнице за ограничено време, и за ограничено време се примењује одређени радијус кривине, те се центрифугалне и Ојлерове силе могу анализирати на основу кружног кретања са тим полупречником.

Овај резултат за убрзање се слаже са оним раније пронађеним. Међутим, у овом приступу, питање промене полупречника закривљености са с се решава потпуно формално, у складу са геометријском интерпретацијом, али не ослањајући се на њу, чиме се избегавају било каква питања која би горња слика могла да сугерише о занемаривању варијације у ρ.

Пример: кружно кретање

Да бисмо илустровали горње формуле, нека су x, y дати као:

$x=\alpha \cos {\frac {s}{\alpha }}\ ;\ y=\alpha \sin {\frac {s}{\alpha }}\ .$

Онда је:

$x^{2}+y^{2}=\alpha ^{2}\ ,$

које се може препознати као кружна путања око координатног почетка са полупречником α. Положај с = 0 одговара [α, 0] или 3 сата. Да би се користио горњи формализам, потребни су деривати:

$y^{\prime }(s)=\cos {\frac {s}{\alpha }}\ ;\ x^{\prime }(s)=-\sin {\frac {s}{\alpha }}\ ,$

$y^{\prime \prime }(s)=-{\frac {1}{\alpha }}\sin {\frac {s}{\alpha }}\ ;\ x^{\prime \prime }(s)=-{\frac {1}{\alpha }}\cos {\frac {s}{\alpha }}\ .$

Са овим резултатима, може се потврдити да:

$x^{\prime }(s)^{2}+y^{\prime }(s)^{2}=1\ ;\ {\frac {1}{\rho }}=y^{\prime \prime }(s)x^{\prime }(s)-y^{\prime }(s)x^{\prime \prime }(s)={\frac {1}{\alpha }}\ .$

Јединични вектори се такође могу наћи:

$\mathbf {u} _{\mathrm {t} }(s)=\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]\ ;\ \mathbf {u} _{\mathrm {n} }(s)=\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]\ ,$

који служе да се покаже да се с = 0 налази на позицији [ρ, 0] и с = ρπ/2 ат [0, ρ], што се слаже са оригиналним изразима за x и y. Другим речима, с се мери у супротном смеру од казаљке на сату око круга од 3 сата. Такође, могу се наћи деривати ових вектора:

${\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {t} }(s)=-{\frac {1}{\alpha }}\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]=-{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ;$

$\ {\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {n} }(s)={\frac {1}{\alpha }}\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]={\frac {1}{\alpha }}\mathbf {u} _{\mathrm {t} }(s)\ .$

За добијање брзине и убрзања неопходна је временска зависност за с. За кретање супротно од казаљке на сату при променљивој брзини в(т):

$s(t)=\int _{0}^{t}\ dt^{\prime }\ v(t^{\prime })\ ,$

где је в(т) брзина и т време, и с(т = 0) = 0. Онда је:

$\mathbf {v} =v(t)\mathbf {u} _{\mathrm {t} }(s)\ ,$

$\mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)+v{\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-v{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} s}{\mathrm {d} t}}$

$\mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ,$

где је већ утврђено да је α = ρ. Ово убрзање је стандардни резултат за неуједначено кружно кретање.

Види још

• Центрифугална сила
• Угаона брзина

Литература

• Серwаy, Раyмонд А.; Јеwетт, Јохн W. (2004). Пхyсицс фор Сциентистс анд Енгинеерс (6тх изд.). Броокс/Цоле. ИСБН 978-0-534-40842-8. 
• Типлер, Паул (2004). Пхyсицс фор Сциентистс анд Енгинеерс: Мецханицс, Осциллатионс анд Wавес, Тхермодyнамицс (5тх изд.). W. Х. Фрееман. ИСБН 978-0-7167-0809-4. 
• Центрипетал форце вс. Центрифугал форце, фром ан онлине Регентс Еxам пхyсицс туториал бy тхе Осwего Цитy Сцхоол Дистрицт
• Ланцзос, Цорнелиус (1970). Тхе вариатионал принциплес оф мецханицс (4тх изд.). Неw Yорк: Довер Публицатионс Инц. Интродуцтион, пп. xxи–xxиx. ИСБН 0-486-65067-7. 
• Сyнге, Ј. L. (1960). „Цлассицал дyнамицс”. Ур.: Флüгге, С. Принциплес оф Цлассицал Мецханицс анд Фиелд Тхеорy / Принзипиен дер Классисцхен Мецханик унд Фелдтхеорие. Енцyцлопедиа оф Пхyсицс / Хандбуцх дер Пхyсик. 2 / 3 / 1. Берлин, Хеиделберг: Спрингер Берлин Хеиделберг. ИСБН 978-3-540-02547-4. ОЦЛЦ 165699220. дои:10.1007/978-3-642-45943-6. 
• Арнолʹд, VI (1989). Матхематицал метходс оф цлассицал мецханицс (2нд изд.). Спрингер. Цхаптер 8. ИСБН 978-0-387-96890-2. 
• Доран, C; Ласенбy, А (2003). Геометриц алгебра фор пхyсицистс. Цамбридге Университy Пресс. стр. §12.3, пп. 432–439. ИСБН 978-0-521-71595-9. 
• Меррифиелд, Мицхаел. „γ – Лорентз Фацтор (анд тиме дилатион)”. Сиxтy Сyмболс. Брадy Харан фор тхе Университy оф Ноттингхам. 
• Меррифиелд, Мицхаел. „γ2 – Гамма Релоадед”. Сиxтy Сyмболс. Брадy Харан фор тхе Университy оф Ноттингхам. 
• Гомез, Р W; Хернандез-Гомез, Ј Ј; Марqуина, V (25. 7. 2012). „А јумпинг цyлиндер он ан инцлинед плане”. Еур. Ј. Пхyс. ИОП. 33 (5): 1359—1365. Бибцоде:2012ЕЈПх...33.1359Г. С2ЦИД 55442794. арXив:1204.0600 . дои:10.1088/0143-0807/33/5/1359. Приступљено 25. 4. 2016. ЦС1 одржавање: Формат датума (веза)

Спољашње везе

• Notes from University of Winnipeg
• Notes from Physics and Astronomy HyperPhysics at Georgia State University; see also home page
• Notes from Britannica
• Notes from PhysicsNet
• NASA notes by David P. Stern
• Notes from U Texas.
• Analysis of smart yo-yo
• The Inuit yo-yo
• Kinematic Models for Design Digital Library (KMODDL)