Хеш функција

Хеш функција која слика имена у целе бројеве у опсегу од 0-15. Долази до колизије у случајевима "Јохн Смитх" и "Сандра Дее".

Хеш функција је сваки алгоритам који подацима произвољне дужине додељује податке фиксне дужине.

Вредност коју враћа хеш функција зове се хеш вредност или хеш код.

Опис

Хеш функције се првенствено користе за генерисање фиксне дужине излазних података који се понашају као референце на оригиналне податке. Ово је корисно када су оригинални подаци сувише гломазни да би се користили у целости. Једна практицна примена је структура података која се зове хеш табела у којој су подаци смештени асоцијативно. Линеарна претрага имена особе у листи траје дуже како се дужина листе повећава, али хеширана вредност може бити складиштити референцу на оригинални податак, па тако добијамо константно време за претрагу.

Друга употреба је у криптографији, науци кодирања и очувања података. Хеш функције представљају основни принцип за ПГП алгоритам за валидацију података. Такође се користе да би се убрзало тражење ставки у базама података, детектовање дуплираних или сличних вредности у великом фајлу и проналажење сличних сегмената у ДНК секвенци. Хеш функција треба да буде детерминистички одредјена, тј. када се два пута позове над идентичним подацима (нпр. две ниске које садрже потпуно исте карактере), функција треба да произведе исту вредност. То је од кључног значаја за исправност готово свих алгоритама на основу хеширања. Хеш функције обично нису инвертибилне, што значи да није могуће реконструисати улазну вредност x само из њене хеш вредности х(x). У многим апликацијама уобичајено је да се неколико различитих вредности слика у исту хеш вредност и то стање зовемо хеш колизијама. Ови судари могу изазвати забуну медју објектима, што може допринети да алгоритми раде спорије и да буду мање прецизни. Хеш функције су дизајниране тако да се што више смањи вероватноћа судара. За криптографске намене, хеш функције су пројектоване на такав начин да је немогуће реконструисати било какав улаз само из хеш функције, без трошења великог рачунарског времена.

Употреба

Хеш табеле

Хеш функције се првенствено користе у хеш табелама, да се брзо пронађе податак (дефиниција у речнику нпр.) ако имамо дат кључ, односно реч чије значење тражимо. Претпоставимо да је дато н кључева из скупа У величине |У|=M>>н. Идеја је да кључеве сместимо у табелу величине м, тако да м није много веће од н. Конкретно, потребно је дефинисати функцију х: {0, 1, ... , M-1} -> {0, 1, ... , м-1}, хеш функцију, која за сваки податак одређује његову позицију на основу вредности одговарајућег кључа. Типично, домен хеш функција (скуп могућих кључева) је већи од свог опсега (броја раличитих индекса табеле), тако да се више различитих кључева пресликава у исти индекс. Дакле, потребно је решити два проблема: налажење хеш функција које минимизирају могућност појаве колизија и поступак за обраду колизија када до њих ипак дође. Иако је величина M скупа У много већа од величине табеле м, стварни скуп кључева које треба обрадити обично није велики. Добра хеш функција пресликава кључеве равномерно по табели - да би се минимизирала могућност колизија проузрокованих нагомилавањем кључева у неким областима табеле. У просеку се у сваку локацију табеле овако изабраном хеш функцијом пресликава велики број (из скупа свих могућих) кључева, њих M/м. Хеш функција треба да трансформише скуп кључева равномерно у скуп случајних локација из скупа {0, 1, ... , м-1}. Униформност и случајност су битне особине хеш функције. Тако, на пример, погрешно је за хеш функцију од 13-цифреног матичног броја узети број који чине пета, шеста и седма цифра матичног броја: те три цифре су три најниже цифре године рођења, па за било коју величину групе студената узимају мање од десетак различитих вредности од 1000 могућих. Ако је величина табеле м прост број, а кључеви су цели бројеви, онда је једноставна и добра хеш функција дата изразом х(x)=x мод м. Ако пак м није прост број (нпр. м=2^к), онда се може користити функција х(x)=(x мод п) мод м, где је п прост број такав да је м<<п<<M. Неугодна је ситуација кад су сви кључеви облика р + к * п за неки цели број р, јер ће сви кључеви имати исту вредност хеш функције р. Тада има смисла увести још један ниво рандомизације, тиме што би се сама хеш функција бирала на случајан начин. На пример, број п могао би се бирати са унапред припремљене листе простих бројева. Друга могућност је да се користе хеш функције облика х(x) = (аx + б мод п) мод м, где су а≠0 и б случајно изабрани бројеви мањи од п. Вредности ове функције се израчунавају на сложенији начин, али је њена предност да је у просеку добра за све улазе. Разуме се да се за све приступе у истој табели мора користити иста хеш функција. У много случајева потребно је више независних хеш табела, или се табеле често креирају и бришу. Тада се за сваку нову табелу може користити друга хеш функција.

Кеш

Хеш функције се такође користе за изградњу кешева за велике скупове података ускладиштених у спорим медијима. Кеш је генерално једноставнији од хеш табеле за претрагу, пошто сваки судар може да се реши одбацивањем старије од две сударајуће ставке.

Блумов филтер

Хеш функције су есенцијални састојак у Блумовом филтеру, структури података која се користи да се утврди да ли елемент припада датом скупу.

Проналажење дуплираних записа

Када се складиште записи у великој обичној датотеци, може се користити хеш функција да сваком податку додели индекс у табели Т и да сакупи у исти низ Т[и] листу бројева свих података са истом хеш вредности и. Када се табела попуни, сви дупликати податка ће завршити у истом низу. Дупликати се онда могу наћи читањем сваког низа Т[и] који садржи два или више елемента, њиховим преузимањем и поредјењем. Са табелом одговарајуће величине, вероватно је да ће овај метод бити много бржи него алтернативни приступи као што су сортирање датотеке и упоређивање свих узастопних парова.

Заштита података

Хеш вредност у криптографији је број генерисан из ниски текста. Хеш вредност је знатно мања од самог текста и генерисана је хеш алгоритмом на такав начин да је вероватноћа да неки други текст има исту хеш вредност занемарљива.

Проналажење сличних записа

Хеш функције се такође могу користити да лоцирају податке чији су кључеви слични, али не и идентични датом кључу или парове података у дугачкој датотеци који имају сличне кључеве. За ту намену потребна је хеш функција која додељује сличне кључеве хеш вредностима који се разликују највише до м, где је м мали цео број (1,2). Ако формирамо табелу Т са бројевима свих података, користећи такву хеш функцију, онда ће слични подаци завршити у истом или у суседном низу. Онда само треба проверити податке у сваком низу Т[и] и оне у низовима Т[и+к], где се к креће од -м до м. Ово се такође користи у алгоритмима који проналазе сличне делове аудио записа у великој колекцији аудио записа. За ово је потребно да хеш функција буде неосетљива на грешке у преносу података и на тривијалне промене као што су јачина звука и компресија.

Проналажење сличних подниски

Иста техника се може користити да се пронађу једнаки или слични сегменти у великим колекцијама ниски. У овом случају улазна ниска се дели на више мањих делова и хеш функција се користи за детектовање потенцијално једнаких делова, као горе. Рабин-Карп алгоритам је релативно брз алгоритам који претражује ниске у просечном времену О(н). Базиран је на коришћењу хеширања при поређењу ниски.

Геометријска хеширања

Овај принцип се широко користи у компјутерској графици, рачунарској геометрији и многим другим дисциплинама, при решавању многих проблема у равни и простору, као што су проналажење најближих парова у скупу тачака, сличних облика, сличних слика у базама података итд. У овим апликацијама, скуп свих улаза је нека врста метричког простора, а хеш функција дели тај простор на мрежу ћелија. Геометријско хеширање се такође користи у телекомуникацијама за кодирање и компресију мултидимензионалних сигнала.

Стандардна употреба хеширања у криптографији

Неке стандардне апликације које користе хеш функције укључују аутентификацију, интегритет порука, откривање корумпираних података и ефикасност дигиталног потписа.

Особине хеш фукције

Детерминизам

Поступак хеширања мора бити детерминистички одређен, тј. за сваку улазну вредност мора да се генерише иста хеш вредност. Овај услов искључује хеш функције које зависе од спољашних параметара , као што су генератори псеудо-случајних бројева. Такодје су искључене функције које зависе од меморијске локације објекта који се хешира, зато што његова адреса приликом извршавања може да се промени (на системима који користе неке методе сакупљача отпадака нпр.).

Униформност

Свака хеш вредност треба да се генерише са приближно истом вероватноћом. Разлог за то је што се трошкови хеширања повећавају како број колизија расте. Хеш табеле често садрже само мали подскуп важећих улаза. На пример, листа чланова неког клуба ће садржати само стотинак имена, од веома великог скупа свих могућих имена. У овим случајевима, критеријум униформности треба да важи за све типичне подскупове улаза који се могу наћи у табели, не само за глобални сет свих могућих улаза.

Опсег променљивих

У многим апликацијама, опсег хеш вредности може бити различит при сваком покретању програма, или може да се промени прликом самог извршавања (нпр. када хеш табела треба да се прошири). У тим ситуацијама потребна нам је хеш функција која узима два параметра - улазни податак з и број н дозвољених хеш вредности.

Када се хеш функција користи за чување вредности у хеш табели које живе ван извршавања програма или када хеш табела треба да се прошири или смањи, хеш табела се назива динамичком хеш табелом.

Нормализација података

У неким апликацијама, улазни подаци могу садрзати карактеристике које су ирелевантне за потребе поређења. На пример, када претражујемо име особе, пожељно би било да се игнорише разлика између великих и малих слова. Такви подаци, ако се сматрају еквивалентним, морају имати исту хеш вредност. Ово се може постићи нормализацијом улаза пре његовог хеширања, нпр. пребацивањем свих слова у велика.

Континуитет

Хеш фукција која се користи при претрази сличних података који се сматрају еквивалентним, мора бити континуална што је више могуће. Два улаза која се мало разликују морају се сликати у исту или приближно исту хеш вредност. Требати имати на уму да се континуалност може сматрати фаталном грешком у криптографији и сличним концептима. Континуалност је пожељна за хеш функције које се користе само у неким апликацијама, као што су хеш табеле у којима се тражи најближи сусед датог податка.

Агоритми хеш функција

За већину типова функција хеширања избор функције зависи од природе улазних података и вероватноће њиховог коришћења у намераваној апликацији.

Тривијална хеш функција

Ако је податак који треба да се хешира довољно мали, онда се као хеш вредност може користити сам податак (представљен као цео број у бинарној нотацији). Трошак израчунавања ове функције ефективно је нула и ова хеш функција је савршена (идентитет). Значење "довољно мали" зависи од величине типа који се користи као хеширана вредност. На пример, у Јави, хеш код је 32-битни цео број, тако да 32-битни објекат класе Интегер и 32-битни објекат класе Флоат могу једноставно директно да се користе као хеш вредности, док 64-битни објекти обе класе не могу да користе овај метод.

Савршена хеш функција

Савршена хеш функција за четири имена

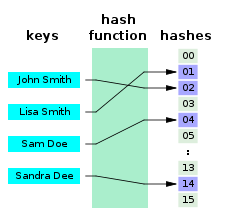
За хеш функцију која је ињективна (сваки валидан улаз додељује разлицитој хеш вредности), кажемо да је савршена. Са таквом функцијом можемо директно лоцирати жељени улаз у хеш табели, без додатног тражења.

Минимално савршено хеширање

Минимална хеш функција за четири имена

За савршену функцију од н кључева кажемо да је минимална ако се њен опсег састоји од н узастопних целих бројева, обично од 0 до н-1. Поред тога што је потребан један корак за проналажење, минимална савршена функција даје компактну хеш табелу, без празних поља. Минималне савршене функције је много теже пронаћи него оне савршене са ширим опсегом.

Хеширање униформно распоређених података

Ако су улази ниске фиксне дужине и сваки улаз може самостално доћи са униформном вероватноћом (као што су телефонски бројеви, бројеви регистарских таблица и слично), тада хеш функција сваком броју грубо додељује своју хеш вредност. На пример, претпоставимо да је сваки улаз цео број з у опсегу од 0 до Н-1, а излаз х мора бити у опсегу од 0 до н-1, где је Н много веће од н. Тада би се хеш функција могла дефинисати као х = з мод н или х = (з * н) / Н. Ове једноставне формуле неце радити ако улазне вредности нису једнаке или независне. На пример, корисници једног супермаркета ће да живе у истој географској области, тако да је вероватно да ће њихови бројеви поцињати са 3 или 4 исте цифре. У том случају, ако је м 10000 или слично, формула (з * м) / M која зависи углавном од водећих цифара ће да генерисе много колизија.

Хеширање података променљиве дужине

Када су подаци дугачки карактерски низови - као лична имена, адресе wеб страница, њихова дистрибуција је обично врло неуједначена, са компликованим зависностима. На пример текст на било ком језику има неуниформну расподелу карактера. За овакве податке мудро је користити хеш функцију која зависи од сваког карактера на другачији начин. У криптографији се користи Меркле Дамград кострукција. Схема за хеширање оваквих података јесте да се разбије улаз на низ мањих једница (битова, бајтова, речи) и да се комбинују те једнице б[1], б[2], ... , б[м] секвенцијално, као што следи:

S ← S0; //inicijalizuje se stanje
for k in 1, 2, .. m do //učitavaju se ulazne jedinice
  S ← F(S, b[k]);        // kombinovanje jedinice b[k] sa stanjem
return G(S, n)

Стање варијабле С може бити 32-битни или 64-битни неозначени цео број. У том случају С0 може бити 0, а Г(С,н) може бити само С мод н. Најбољи избор за Ф је комплексни проблем и зависи од природе података. Ако су једнице б[к] појединачни битови, онда Ф(С,б) може бити, на пример:

if najvišibit(S) = 0 then
   return 2 * S + b
 else
   return (2 * S + b) ^ P

Овде највишиБит(С) означава најзначајнији бит С; оператор * означава целобројно множење без прекорачења, ^ је битовска ексклузивна дисјункција која се примењује на речи, а П је погодна фиксна реч.

Наменске хеш функције

У многим случајевима се могу дизајнирати хеш функције које дају много мање судара него фунцкија опште намене. На пример, претпоставимо да су улазни подаци имена фајлова као што су ФИЛЕ0000.ЦХК, ФИЛЕ0001.ЦХК, ФИЛЕ0002.ЦХК. За такве податке, функција која издваја нумерички део к из имена фајла и враћа к мод н била би скоро оптимална.

Ролинг хеш

У неким апликацијама, као што су претраге подниски, мора да се израчуна функција х за сваки к-ти карактер подниске, датог н-тог карактера ниске т, где је к фиксирани цео број, а н је к. Решење да се овде издвоји свака подниска с од т и да се посебно израчуна х(с) за сваку подниску, захтева к * н операција. Али одговарајућим избором х, техника ролинг хеша може да се користи при израчунавању вредности са трудом пропорционалним к + н.

Универзално хеширање

Схема универзалног хеширања је рандомизирани алгоритам који бира хеш функције х медју фамилијом функција таквих да је вероватноћа колизија било која два раличита кључа 1/н, где је н број различитих хеш вредности независан од та два кључа. Оно нам омогућава (у смислу вероватноће) да се хеш функција понаша као да смо користили рандом функцију, за било какве улазне податке. Како год, имаћемо много више колизија него код савршеног хеширања и вероватно ће нам требати више операција него код хеш функције специјалне намене.

Ефикасно хеширање ниски

Модерни микропроцесори ће омогућити много бржу обраду, ако 8-битне карактерске ниске нису хеширане обрадом једног карактера у једном тренутку, већ ако се посматрају као низови 32-битних или 64-битних целих бројева и хеширањем/уситњавањем ових великих речи путем аритметичких операција (множењем константом и шифтовањем битова). Преостали карактери ниске који су мањи од дужине речи, процесор мора да обради другачије (обрадом појединачних карактера). За овај приступ је доказано да повећава брзину генерисања хеш кода пет или више пута на модерним микропроцесорима, са величином речи од 64 бита. Други приступ је да се конвертују ниске у 32-битне или 64-битне нумеричке вредности, а онда применити хеш функцију. Један од метода којим може да се избегне проблем јер ниске имају велику сличност (Аааааааа и Аааааааб), јесте да се користи цикличка провера редунданси (ЦРЦ алгоритам) над ниском, како би се израчунале 32-битне или 64-битне вредности. Иако је могуће да две различите ниске имају исти ЦРЦ, вероватноћа је веома мала. ЦРЦ приступ ради за ниске произвољне дужине.

Локално-осетљиво хеширање

Овде је основна идеја да се хеширају улазне ставке, тако да се оне сличне сликају у исте сегменте са великом вероватноћом (број сегмената је много мањи од броја могућих улазних ставки). Овде је циљ да се максимизује вероватноћа колизија сличних ставки, за разлику од конвенционалних хеш функција, где је основни мотив да се колизије избегну.

Порекло термина

Термин хеш долази аналогно свом не-техничком значењу - "исецкати и помешати". I заиста, типична хеш функција ради као мод оператор, "сецка" улазни домен на много под-домена који бивају измешани у излазном опсегу како би се побољшала униформност. Доналд Кнут напомиње да је Ханс Питер Лун из ИБМ-а првобитно користио овај концепт у меморандуму из јануара 1953, а да је Роберт Морис користио термин у истраживачком раду у ЦАЦМ-у, што је произвело да термин из техничког жаргона уђе у формалну терминологију.

Spoljašnje veze

• Hash Functions and Block Ciphers by Bob Jenkins
• = 25. 10. 2009+21:06:51 The Goulburn Hashing Function (PDF) by Mayur Patel
• Hash Function Construction for Textual and Geometrical Data Retrieval Latest Trends on Computers, Vol.2. стр. 483–489, CSCC conference, Corfu, 2010
• Algoritmi, Miodrag Živković