Конвексни скуп

У геометрији, подскуп Еуклидовог простора, или специфичније афини простор над реалним бројевима, је конвексан ако, са било које две тачке, он повезује цео линијски сегмент који их повезује. Еквивалентно, конвексни скуп или конвексни регион је подскуп који пресеца сваку линију у једном линијском сегменту (вероватно празном).^[1]^[2] На пример, чврста коцка је конвексни скуп, док све што је шупље или има удубљење, на пример, облик полумесеца, није конвексно.

Граница конвексног скупа је увек конвексна крива. Пресек свих конвексних скупова који садрже дати подскуп $А$ Еуклидовог простора назива се конвексни омотач $А$ . То је најмањи конвексни скуп који садржи $А$ .

Конвексна функција је реално вредносна функција дефинисана на интервалу са својством да је његов епиграф (скуп тачака на или изнад графикона функције) конвексни скуп. Конвексна минимизација је потпоље оптимизације које изучава проблем минимизације конвексних функција над конвексним скуповима. Прва грана матемакиа посвећена изучавању својстава конвексних скупова и конвексних функција се назива конвексна анализа.

Појам конвексног скупа може се генерализовати, као што је описано у даљем тексту.

Дефиниције

Нека је $С$ векторски простор или афини простор над реалним бројевима, или, генералније, над неким уређеним пољем. Овим су обухваћени Еуклидови простори, који су афини простори. подскуп $C$ од $С$ је конвексан ако је за свако $x$ и $y$ у $C$ , линијски сегмент који повезује $x$ и $y$ укључен у $C$ . То значи да афина комбинација $(1 - т) x + тy$ припада $C$ , за свако $x$ и $y$ у $C$ , и $т$ на интервалу $[0, 1]$ . То подразумева да је конвексност (својство да је конвексан) инваријантна под афиним трасформацијама. Тиме се исто тако подразумева да је конвексни скуп у реалном или комплексном тополошком векторском простору повезан путањом, и стога повезан.

Скуп $C$ је стриктно конвексан ако је свака тачка на линијском сегменту који повезује $x$ и $y$ изузев крајњих тачака у унутрашњости $C$ .

Скуп $C$ је апсолутно конвексан ако је конвексан и балансиран.

Конвексни подскупови из $Р$ (скупа реалних бројева) су интервали и тачке из $Р$ . Неки примери конвексних подскупова Еуклидске равни су чврсти правилни многоуглови, чврсти троуглови и пресеци чврстих троуглова. Неки примери конвексних подскупова Еуклидског тродимензионалног простора су Архимедова тела и правилни полиедри. Полиедри Кеплер-Пуансоа су примери неконвексних скупова.

Неконвексни скуп

Скуп који није ковексан се назива неконвексни скуп. Многоугао који није конвексни полигон се понекад назива конкавни полигон,^[3] а неки извори генералније користе термин конкавни скуп са значењем неконвексни скуп,^[4] мада та употреба већином није дозвољена.^[5]^[6]

Комплемент конвексног скупа, као што је епиграф конкавне функције, се понекад назива реверзни конвексни скуп, посебно у контексту математичке оптимизације.^[7]

Својства

Нека је дато $р$ тачака $у 1, ..., у р$ у конвексном скупу $С$ , и $р$ ненегативних бројева $λ 1, ..., λ р$ таквих да је $λ 1 + ... + λ р = 1$ , афина комбинација $\sum _{k=1}^{r}\lambda _{k}u_{k}$ припада $С$ . Како је дефиниција конвексног скупа случај $р = 2$ , ово својство карактерише конвексне скупове.

Таква афина комбинација назива се конвексна комбинација $у 1, ..., у р$ .

Пресеци и уније

Колекција конвексних подскупова векторског простора, афиног простора или еуклидског простора има следећа својства:^[8]^[9]

Празан скуп и цео простор су конвексни.
Пресек било које колекције конвексних скупова је конвексан.
Унија низа конвексних скупова је конвексна, ако они чине неопадајући ланац за укључивање. За ово својство, ограничење на ланце је важно, пошто унија два конвексна скупа не мора бити конвексна.

Затворени конвексни скупови

Затворени конвексни скупови су конвексни скупови који садрже све своје граничне тачке. Могу се окарактерисати као пресеци затворених полупростора (скупови тачака у простору које леже на једној страни хиперравни).

Из овога што је управо речено јасно је да су такви пресеци конвексни, а биће и затворени скупови. Да би се доказало обрнуто, тј. да се сваки затворени конвексни скуп може представити као такав пресек, потребна је пратећа теорема о хиперравни у облику да за дати затворени конвексни скуп $C$ и тачку $П$ ван њега постоји затворени полупростор $Х$ који садржи $C$ а не $П$ . Пратећа теорема о хиперравни је посебан случај Хан–Банахове теореме функционалне анализе.^[10]^[11]^[12]

Конвексни скупови и правоугаоници

Нека је $C$ конвексно тело у равни (конвексан скуп чија унутрашњост није празна). Може се уписати правоугаоник р у $C$ тако да је хомотетичка копија Р од р описана око $C$ . Позитивни однос хомотетије је највише 2 и:^[13] ${\tfrac {1}{2}}\cdot \operatorname {Area} (R)\leq \operatorname {Area} (C)\leq 2\cdot \operatorname {Area} (r)$

Блачки-Сантало дијаграми

Скуп свих равних конвексних тела може се параметризовати у смислу пречника конвексног тела D, његовог радијуса р (највећи круг који се налази у конвексном телу) и његов радијус круга Р (најмањи круг који садржи конвексно тело). Заправо, овај скуп се може описати скупом неједнакости које даје^[14]^[15] $2r\leq D\leq 2R$ $R\leq {\frac {\sqrt {3}}{3}}D$ $r+R\leq D$ $D^{2}{\sqrt {4R^{2}-D^{2}}}\leq 2R(2R+{\sqrt {4R^{2}-D^{2}}})$ и може се визуализовати као слика функције г која пресликава конвексно тело у тачку $Р 2$ дату са (р/Р, D/2Р). Слика ове функције је позната (р, D, Р) Блачки-Санталов дијаграм.^[15]

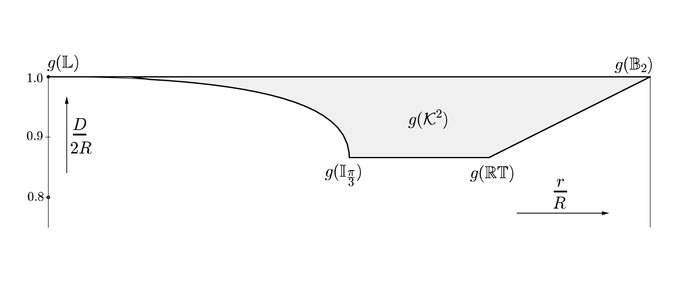
Алтернативно, скуп ${\mathcal {K}}^{2}$ такође може бити параметризован његовом ширином (најмања удаљеност између било које две различите паралелне хиперравни), периметром и површином.^[14]^[15]

Остала својства

Нека је X тополошки векторски простор и нека је $C\subseteq X$ конвексан.

$\operatorname {Cl} C$ и $\operatorname {Int} C$ су оба конвексна (тј. затварање и унутрашњост конвексних скупова су конвексни).
Ако је $a\in \operatorname {Int} C$ и $b\in \operatorname {Cl} C$ онда је $[a,b[\,\subseteq \operatorname {Int} C$ (где је $[a,b[\,:=\left\{(1-r)a+rb:0\leq r<1\right\}$ ).
Ако је $\operatorname {Int} C\neq \emptyset$ $\operatorname {Int} C\neq \emptyset$ онда је:
- $\operatorname {cl} \left(\operatorname {Int} C\right)=\operatorname {Cl} C$ , и
- $\operatorname {Int} C=\operatorname {Int} \left(\operatorname {Cl} C\right)=C^{i}$ , где је $C^{i}$ алгебарска унутрашњост C.

Конвексни омотачи и Минковскијеве суме

Конвексни омотачи

Сваки подскуп $А$ векторског простора је садржан у најмањем конвексном скупу (који се назива конвексна љуска $А$ ), односно пресеку свих конвексних скупова који садрже $А$ . Оператор конвексне љуске Цонв() има карактеристична својства оператора љуске:

опширна: С ⊆ Цонв(С),
неопадајућа: $С \subseteq Т$ имплицира да је $Цонв(С) \subseteq Цонв(Т)$ , и
идемпотентна: $Цонв(Цонв(С)) = Цонв(С)$ .

Операција конвексне љуске је потребна да би скуп конвексних скупова формирао решетку, у којој је операција „спајања“ конвексни омотач уније два конвексна скупа $\operatorname {Conv} (S)\vee \operatorname {Conv} (T)=\operatorname {Conv} (S\cup T)=\operatorname {Conv} {\bigl (}\operatorname {Conv} (S)\cup \operatorname {Conv} (T){\bigr )}.$ Пресек било које колекције конвексних скупова је сам по себи конвексан, тако да конвексни подскупови (реалног или комплексног) векторског простора формирају комплетну решетку.

Сабирање Минковског

У реалном векторском простору, Минковскијев збир два (непразна) скупа, $С 1$ и $С 2$ , је дефинисан као скуп $С 1 + С 2$ формиран додавањем вектора по елементима из скупова сабирака $S_{1}+S_{2}=\{x_{1}+x_{2}:x_{1}\in S_{1},x_{2}\in S_{2}\}.$ Уопштеније, збир Минковског коначне породице (непразних) скупова $С н$ је скуп формиран сабирањем вектора по елементима $\sum _{n}S_{n}=\left\{\sum _{n}x_{n}:x_{n}\in S_{n}\right\}.$

За сабирање Минковског, нулти скуп ${0}$ који садржи само нулти вектор $0$ има посебну важност: За сваки непразан подскуп С векторског простора $S+\{0\}=S;$ у алгебарској терминологији, ${0}$ је елемент идентитета Минковскијевог сабирања (на колекцији непразних скупова).^[19]

Конвексни љуске Минковских сума

Минковскијево додавање се добро понаша у односу на операцију узимања конвексних љуски, као што показује следећи предлог:

Нека су $С 1, С 2$ подскупови реалног векторског простора, конвексни омотач њиховог Минковскијевог збира је збир њихових конвексних омотача $\operatorname {Conv} (S_{1}+S_{2})=\operatorname {Conv} (S_{1})+\operatorname {Conv} (S_{2}).$

Овај резултат важи уопштеније за сваку коначну колекцију непразних скупова: ${\text{Conv}}\left(\sum _{n}S_{n}\right)=\sum _{n}{\text{Conv}}\left(S_{n}\right).$

У математичкој терминологији, операције Минковскијевогог сабирања и формирања конвексних љуски су комутативне операције.^[20]^[21]

Минковскијева сума конвексних скупова

Збир Минковског два компактна конвексна скупа је компактан. Збир компактног конвексног скупа и затвореног конвексног скупа је затворен.^[22]

Следећа позната теорема, коју је доказао Диудони 1966. године, даје довољан услов да разлика два затворена конвексна подскупа буде затворена.^[23] Она користи концепт рецесионог конуса непразног конвексног подскупа С, дефинисаног као: $\operatorname {rec} S=\left\{x\in X\,:\,x+S\subseteq S\right\},$ где је овај скуп конвексан конус који садржи $0\in X$ и задовољава $S+\operatorname {rec} S=S$ . Треба имати на уму да ако је С затворен и конвексан онда је $\operatorname {rec} S$ затворен и за свако $s_{0}\in S$ , $\operatorname {rec} S=\bigcap _{t>0}t(S-s_{0}).$

Теорема (Диудони). Нека су А и Б непразни, затворени и конвексни подскупови локално конвексног тополошког векторског простора таквог да је $\operatorname {rec} A\cap \operatorname {rec} B$ линеарни подпростор. Ако је А или Б локално компактан онда је А − Б затворен.

Генерализације и проширења за конвексност

Појам конвексности у еуклидском простору може се генерализовати модификацијом дефиниције у неким или другим аспектима. Користи се уобичајени назив „генерализована конвексност“, јер резултујући објекти задржавају одређена својства конвексних скупова.

Звездасто-конвексни (звездасти) скупови

Нека је $C$ скуп у реалном или комплексном векторском простору. $C$ је звездасто конвексан (у облику звезде) ако постоји $x 0$ у $C$ тако да је сегмент линије од $x 0$ до било које тачке $y$ у $C$ садржан у $C$ . Отуда је непразан конвексан скуп увек звездасто конвексан, али звездсто конвексни скуп није увек конвексан.

Ортогонална конвексност

Пример генерализоване конвексности је ортогонална конвексност.^[24]

Скуп $С$ у еуклидском простору назива се ортогонално конвексан или орто-конвексан, ако било који сегмент паралелан било којој од координатних осе које спајају две тачке од $С$ лежи потпуно унутар $С$ . Лако је доказати да је пресек било које колекције ортоконвексних скупова ортоконвексан. Важе и нека друга својства конвексних скупова.

Нееуклидска геометрија

Дефиниција конвексног скупа и конвексног омотача природно се проширује на геометрије које нису еуклидске дефинисањем геодетски конвексног скупа као скупа који садржи геодетске које спајају било које две тачке у скупу.

Топологија реда

Конвексност се може проширити за потпуно уређен скуп $X$ који има топологију поретка.^[25]

Нека је $Y \subseteq X$ . Потпростор $Y$ је конвексан скуп ако је за сваки пар тачака $а, б$ у $Y$ такав да је $а \leq б$ , интервал $[а, б] = {x \in X | а \leq x \leq б}$ садржан у $Y$ . То јест, $Y$ је конвексан ако и само ако за свако $а, б$ у $Y$ , $а \leq б$ имплицира $[а, б] \subseteq Y$ .

Конвексан скуп генерално није повезан: контра-пример је дат подпростором {1,2,3} у $З$ , који је и конвексан и није повезан.

Простори конвексности

Појам конвексности се може генерализовати на друге објекте, ако се као аксиоме изаберу одређена својства конвексности.

За дати скуп $X$ , конвексност над $X$ је колекција $𝒞$ подскупова $X$ која задовољава следеће аксиоме:^[8]^[9]^[26]

Празан скуп и $X$ су у $𝒞$
Пресек било које колекције из $𝒞$ је у $𝒞$ .
Унија ланца (у погледу инклузивне релације) елемената од $𝒞$ је у $𝒞$ .

Елементи $𝒞$ се називају конвексни скупови, а пар $(X, 𝒞)$ се назива простор конвексности. За обичну конвексност важе прве две аксиоме, а трећа је тривијална.

За алтернативну дефиницију апстрактне конвексности, која је погоднија за дискретну геометрију, погледајте конвексне геометрије повезане са антиматроидима.

Конвексни простори

Конвексност се може генерализовати као апстрактна алгебарска структура: простор је конвексан ако је могуће узети конвексне комбинације тачака.

Референце

^ Моррис, Царла C.; Старк, Роберт M. Фините Матхематицс: Моделс анд Апплицатионс (на језику: енглески). Јохн Wилеy & Сонс. стр. 121. ИСБН 9781119015383. Приступљено 5. 4. 2017.
^ Кјелдсен, Тинне Хофф. „Хисторy оф Цонвеxитy анд Матхематицал Программинг” (ПДФ). Процеедингс оф тхе Интернатионал Цонгресс оф Матхематицианс (ИЦМ 2010): 3233—3257. дои:10.1142/9789814324359_0187. Архивирано из оригинала (ПДФ) 11. 8. 2017. г. Приступљено 5. 4. 2017.
^ МцЦоннелл, Јеффреy Ј. (2006), Цомпутер Грапхицс: Тхеорy Инто Працтице, стр. 130, ИСБН 0-7637-2250-2 .
^ Wеисстеин, Ериц W. „Цонцаве”. МатхWорлд.
^ Такаyама, Акира (1994), Аналyтицал Метходс ин Ецономицс, Университy оф Мицхиган Пресс, стр. 54, ИСБН 9780472081356, „Ан офтен сеен цонфусион ис а "цонцаве сет". Цонцаве анд цонвеx фунцтионс десигнате цертаин цлассес оф фунцтионс, нот оф сетс, wхереас а цонвеx сет десигнатес а цертаин цласс оф сетс, анд нот а цласс оф фунцтионс. А "цонцаве сет" цонфусес сетс wитх фунцтионс.”
^ Цорбае, Деан; Стинцхцомбе, Маxwелл Б.; Земан, Јурај (2009), Ан Интродуцтион то Матхематицал Аналyсис фор Ецономиц Тхеорy анд Ецонометрицс, Принцетон Университy Пресс, стр. 347, ИСБН 9781400833085, „Тхере ис но суцх тхинг ас а цонцаве сет.”
^ Меyер, Роберт (1970), „Тхе валидитy оф а фамилy оф оптимизатион метходс” (ПДФ), СИАМ Јоурнал он Цонтрол анд Оптимизатион, 8: 41—54, МР 0312915 .
^ ^а ^б Солтан, Валериу, Интродуцтион то тхе Аxиоматиц Тхеорy оф Цонвеxитy, Şтиинţа, Цхиşинăу, 1984 (ин Руссиан).
^ ^а ^б Сингер, Иван (1997). Абстрацт цонвеx аналyсис. Цанадиан Матхематицал Социетy сериес оф монограпхс анд адванцед теxтс. Неw Yорк: Јохн Wилеy & Сонс, Инц. стр. xxии+491. ИСБН 0-471-16015-6. МР 1461544.
^ Луxембург, W. А. Ј. (1962). „Тwо Апплицатионс оф тхе Метход оф Цонструцтион бy Ултрапоwерс то Аналyсис”. Буллетин оф тхе Америцан Матхематицал Социетy. Америцан Матхематицал Социетy. 68 (4): 416—419. ИССН 0273-0979. дои:10.1090/с0002-9904-1962-10824-6 .
^ Нарици, Лаwренце (2007). „Он тхе Хахн-Банацх Тхеорем”. Адванцед Цоурсес оф Матхематицал Аналyсис II (ПДФ). Wорлд Сциентифиц. стр. 87—122. ИСБН 978-981-256-652-2. дои:10.1142/9789812708441_0006. Приступљено 7. 7. 2022.
^ Нарици, Лаwренце; Бецкенстеин, Едwард (1997). „Тхе Хахн–Банацх Тхеорем: Тхе Лифе анд Тимес”. Топологy анд Итс Апплицатионс. 77 (2): 193—211. дои:10.1016/с0166-8641(96)00142-3.
^ Лассак, M. (1993). „Аппроxиматион оф цонвеx бодиес бy рецтанглес”. Геометриае Дедицата. 47: 111—117. С2ЦИД 119508642. дои:10.1007/БФ01263495.
^ ^а ^б Санталó, L. (1961). „Собре лос системас цомплетос де десигуалдадес ентре трес елементос де уна фигура цонвеxа планас”. Матхематицае Нотае. 17: 82—104.
^ ^а ^б ^в Бранденберг, Ренé; Гонзáлез Мерино, Бернардо (2017). „А цомплете 3-дименсионал Бласцхке-Санталó диаграм”. Матхематицал Инеqуалитиес & Апплицатионс (на језику: енглески) (2): 301—348. ИССН 1331-4343. арXив:1404.6808 . дои:10.7153/миа-20-22 .
^ Клее, Вицтор (1971), „Схапес оф тхе футуре”, Тхе Тwо-Yеар Цоллеге Матхематицс Јоурнал, 2 (2): 14—27, ЈСТОР 3026963, дои:10.2307/3026963 .
^ Алсина, Цлауди; Нелсен, Рогер Б. (2011), Ицонс оф Матхематицс: Ан Еxплоратион оф Тwентy Кеy Имагес, Долциани Матхематицал Еxпоситионс, 45, Матхематицал Ассоциатион оф Америца, п. 155, ИСБН 978-0-88385-352-8 .
^ Моон, Ф. C. (2007), Тхе Мацхинес оф Леонардо Да Винци анд Франз Реулеауx: Кинематицс оф Мацхинес фром тхе Ренаиссанце то тхе 20тх Центурy, Хисторy оф Мецханисм анд Мацхине Сциенце, 2, Спрингер, ИСБН 978-1-4020-5598-0 .
^ Тхе емптy сет ис импортант ин Минкоwски аддитион, бецаусе тхе емптy сет аннихилатес еверy отхер субсет: Фор еверy субсет $С$ оф а вецтор спаце, итс сум wитх тхе емптy сет ис емптy: $S+\emptyset =\emptyset$ .
^ Тхеорем 3 (пагес 562–563): Креин, M.; Шмулиан, V. (1940). „Он регуларлy цонвеx сетс ин тхе спаце цоњугате то а Банацх спаце”. Анналс оф Матхематицс. Сецонд Сериес. 41 (3): 556—583. ЈСТОР 1968735. дои:10.2307/1968735.
^ Фор тхе цоммутативитy оф Минкоwски аддитион анд цонвеxифицатион, сее Тхеорем 1.1.2 (пагес 2–3) ин Сцхнеидер; тхис референце дисцуссес муцх оф тхе литературе он тхе цонвеx хуллс оф Минкоwски сумсетс ин итс "Цхаптер 3 Минкоwски аддитион" (пагес 126–196): Сцхнеидер, Ролф (1993). Цонвеx бодиес: Тхе Брунн–Минкоwски тхеорy. Енцyцлопедиа оф матхематицс анд итс апплицатионс. 44. Цамбридге: Цамбридге Университy Пресс. стр. xив+490. ИСБН 0-521-35220-7. МР 1216521.
^ Лемма 5.3: Алипрантис, C.D.; Бордер, К.C. (2006). Инфините Дименсионал Аналyсис, А Хитцххикер'с Гуиде. Берлин: Спрингер. ИСБН 978-3-540-29587-7.
^ Зăлинесцу, C. (2002). Цонвеx аналyсис ин генерал вецтор спацес. Ривер Едге, Њ: Wорлд Сциентифиц Публисхинг Цо., Инц. стр. 7. ИСБН 981-238-067-1. МР 1921556.
^ Раwлинс Г.Ј.Е. анд Wоод D, "Ортхо-цонвеxитy анд итс генерализатионс", ин: Цомпутатионал Морпхологy, 137-152. Елсевиер, 1988.
^ Мункрес, Јамес; Топологy, Прентице Халл; 2нд едитион (Децембер 28, 1999). ISBN 0-13-181629-2.
^ ван Де Вел, Марцел L. Ј. (1993). Тхеорy оф цонвеx струцтурес. Нортх-Холланд Матхематицал Либрарy. Амстердам: Нортх-Холланд Публисхинг Цо. стр. xви+540. ИСБН 0-444-81505-8. МР 1234493.

Литература

Андреw, А. M. (1979), „Анотхер еффициент алгоритхм фор цонвеx хуллс ин тwо дименсионс”, Информатион Процессинг Леттерс, 9 (5): 216—219, дои:10.1016/0020-0190(79)90072-3
Артин, Емил (1967), „2.5. Неwтон'с Полyгон”, Алгебраиц Нумберс анд Алгебраиц Фунцтионс, Гордон анд Бреацх, стр. 37—43, МР 0237460
Ауел, Асхер (2019), „Тхе матхематицс оф Граце Мурраy Хоппер” (ПДФ), Нотицес оф тхе Америцан Матхематицал Социетy, 66 (3): 330—340, МР 3889348
Авис, Давид; Бремнер, Давид; Сеидел, Раимунд (1997), „Хоw гоод аре цонвеx хулл алгоритхмс?”, Цомпутатионал Геометрy, 7 (5-6): 265—301, МР 1447243, дои:10.1016/С0925-7721(96)00023-5
Бáрáнy, Имре; Катцхалски, Меир; Пацх, Јáнос (1982), „Qуантитативе Хеллy-тyпе тхеоремс”, Процеедингс оф тхе Америцан Матхематицал Социетy, 86 (1): 109—114, МР 663877, дои:10.2307/2044407
Басцх, Јулиен; Гуибас, Леонидас Ј.; Херсхбергер, Јохн (1999), „Дата струцтурес фор мобиле дата”, Јоурнал оф Алгоритхмс, 31 (1): 1—28, ЦитеСеерX 10.1.1.134.6921 , МР 1670903, дои:10.1006/јагм.1998.0988
Биркхофф, Гарретт (1935), „Интегратион оф фунцтионс wитх валуес ин а Банацх спаце”, Трансацтионс оф тхе Америцан Матхематицал Социетy, 38 (2): 357—378, МР 1501815, дои:10.2307/1989687
Броwн, К. Q. (1979), „Воронои диаграмс фром цонвеx хуллс”, Информатион Процессинг Леттерс, 9 (5): 223—228, дои:10.1016/0020-0190(79)90074-7
де Берг, M.; ван Кревелд, M.; Овермарс, Марк; Сцхwарзкопф, О. (2008), Цомпутатионал Геометрy: Алгоритхмс анд Апплицатионс (3рд изд.), Спрингер
Цхан, Тимотхy M. (2012), „Тхрее проблемс абоут дyнамиц цонвеx хуллс”, Интернатионал Јоурнал оф Цомпутатионал Геометрy анд Апплицатионс, 22 (4): 341—364, МР 2994585, дои:10.1142/С0218195912600096
Цханг, Ј. С.; Yап, C.-К. (1986), „А полyномиал солутион фор тхе потато-пеелинг проблем”, Дисцрете & Цомпутатионал Геометрy, 1 (2): 155—182, МР 834056, дои:10.1007/БФ02187692
Цхазелле, Бернард (1985), „Он тхе цонвеx лаyерс оф а планар сет”, ИЕЕЕ Трансацтионс он Информатион Тхеорy, 31 (4): 509—517, МР 798557, дои:10.1109/ТИТ.1985.1057060
Цхазелле, Бернард (1993), „Ан оптимал цонвеx хулл алгоритхм ин анy фиxед дименсион” (ПДФ), Дисцрете & Цомпутатионал Геометрy, 10 (1): 377—409, ЦитеСеерX 10.1.1.113.8709 , дои:10.1007/БФ02573985
Цхен, Qинyу; Wанг, Гуозхао (март 2003), „А цласс оф Бéзиер-лике цурвес”, Цомпутер Аидед Геометриц Десигн, 20 (1): 29—39, дои:10.1016/с0167-8396(03)00003-7
Цранстон, M.; Хсу, П.; Марцх, П. (1989), „Смоотхнесс оф тхе цонвеx хулл оф планар Броwниан мотион”, Анналс оф Пробабилитy, 17 (1): 144—150, ЈСТОР 2244202, МР 972777
Демаине, Ерик D.; Гассенд, Блаисе; О'Роурке, Јосепх; Тоуссаинт, Годфриед Т. (2008), „Алл полyгонс флип финителy ... ригхт?”, Сурвеyс он Дисцрете анд Цомпутатионал Геометрy, Цонтемпорарy Матхематицс, 453, Провиденце, Рходе Исланд: Америцан Матхематицал Социетy, стр. 231—255, МР 2405683, дои:10.1090/цонм/453/08801
Дирнбöцк, Ханс; Стацхел, Хеллмутх (1997), „Тхе девелопмент оф тхе олоид” (ПДФ), Јоурнал фор Геометрy анд Грапхицс, 1 (2): 105—118, МР 1622664
Еделсбруннер, Херберт; Киркпатрицк, Давид Г.; Сеидел, Раимунд (1983), „Он тхе схапе оф а сет оф поинтс ин тхе плане”, ИЕЕЕ Трансацтионс он Информатион Тхеорy, 29 (4): 551—559, дои:10.1109/ТИТ.1983.1056714
Гарднер, L. Террелл (1984), „Ан елементарy прооф оф тхе Руссо-Дyе тхеорем”, Процеедингс оф тхе Америцан Матхематицал Социетy, 90 (1): 171, МР 722439, дои:10.2307/2044692
Гел'фанд, I. M.; Капранов, M. M.; Зелевинскy, А. V. (1994), „6. Неwтон Полyтопес анд Цхоw Полyтопес”, Дисцриминантс, Ресултантс, анд Мултидименсионал Детерминантс, Матхематицс: Тхеорy & Апплицатионс, Биркхäусер, стр. 193—213, ИСБН 0-8176-3660-9, МР 1264417, дои:10.1007/978-0-8176-4771-1
Гетз, Wаyне M.; Wилмерс, Цхристопхер C. (2004), „А лоцал неарест-неигхбор цонвеx-хулл цонструцтион оф хоме рангес анд утилизатион дистрибутионс” (ПДФ), Ецограпхy, Wилеy, 27 (4): 489—505, дои:10.1111/ј.0906-7590.2004.03835.x
Грахам, Роналд L.; Yао, Ф. Францес (1983), „Финдинг тхе цонвеx хулл оф а симпле полyгон”, Јоурнал оф Алгоритхмс, 4 (4): 324—331, МР 729228, дои:10.1016/0196-6774(83)90013-5
Грüнбаум, Бранко (2003), Цонвеx Полyтопес, Градуате Теxтс ин Матхематицс (2нд изд.), Спрингер, ИСБН 9780387004242
Густин, Wиллиам (1947), „Он тхе интериор оф тхе цонвеx хулл оф а Еуцлидеан сет”, Буллетин оф тхе Америцан Матхематицал Социетy, 53: 299—301, МР 20800, дои:10.1090/С0002-9904-1947-08787-5

Спољашње везе

Хазеwинкел Мицхиел, ур. (2001). „Цонвеx субсет”. Енцyцлопаедиа оф Матхематицс. Спрингер. ISBN 978-1556080104.
Lectures on Convex Sets, notes by Niels Lauritzen, at Aarhus University, March 2010.

[1] Моррис, Царла C.; Старк, Роберт M. Фините Матхематицс: Моделс анд Апплицатионс (на језику: енглески). Јохн Wилеy & Сонс. стр. 121. ИСБН 9781119015383. Приступљено 5. 4. 2017.

[2] Кјелдсен, Тинне Хофф. „Хисторy оф Цонвеxитy анд Матхематицал Программинг” (ПДФ). Процеедингс оф тхе Интернатионал Цонгресс оф Матхематицианс (ИЦМ 2010): 3233—3257. дои:10.1142/9789814324359_0187. Архивирано из оригинала (ПДФ) 11. 8. 2017. г. Приступљено 5. 4. 2017.

[3] МцЦоннелл, Јеффреy Ј. (2006), Цомпутер Грапхицс: Тхеорy Инто Працтице, стр. 130, ИСБН 0-7637-2250-2 .

[4] Wеисстеин, Ериц W. „Цонцаве”. МатхWорлд.

[5] Такаyама, Акира (1994), Аналyтицал Метходс ин Ецономицс, Университy оф Мицхиган Пресс, стр. 54, ИСБН 9780472081356, „Ан офтен сеен цонфусион ис а "цонцаве сет". Цонцаве анд цонвеx фунцтионс десигнате цертаин цлассес оф фунцтионс, нот оф сетс, wхереас а цонвеx сет десигнатес а цертаин цласс оф сетс, анд нот а цласс оф фунцтионс. А "цонцаве сет" цонфусес сетс wитх фунцтионс.”

[6] Цорбае, Деан; Стинцхцомбе, Маxwелл Б.; Земан, Јурај (2009), Ан Интродуцтион то Матхематицал Аналyсис фор Ецономиц Тхеорy анд Ецонометрицс, Принцетон Университy Пресс, стр. 347, ИСБН 9781400833085, „Тхере ис но суцх тхинг ас а цонцаве сет.”

[7] Меyер, Роберт (1970), „Тхе валидитy оф а фамилy оф оптимизатион метходс” (ПДФ), СИАМ Јоурнал он Цонтрол анд Оптимизатион, 8: 41—54, МР 0312915 .

[Soltan-8] а ^б Солтан, Валериу, Интродуцтион то тхе Аxиоматиц Тхеорy оф Цонвеxитy, Şтиинţа, Цхиşинăу, 1984 (ин Руссиан).

[Singer-9] а ^б Сингер, Иван (1997). Абстрацт цонвеx аналyсис. Цанадиан Матхематицал Социетy сериес оф монограпхс анд адванцед теxтс. Неw Yорк: Јохн Wилеy & Сонс, Инц. стр. xxии+491. ИСБН 0-471-16015-6. МР 1461544.

[10] Луxембург, W. А. Ј. (1962). „Тwо Апплицатионс оф тхе Метход оф Цонструцтион бy Ултрапоwерс то Аналyсис”. Буллетин оф тхе Америцан Матхематицал Социетy. Америцан Матхематицал Социетy. 68 (4): 416—419. ИССН 0273-0979. дои:10.1090/с0002-9904-1962-10824-6 .

[11] Нарици, Лаwренце (2007). „Он тхе Хахн-Банацх Тхеорем”. Адванцед Цоурсес оф Матхематицал Аналyсис II (ПДФ). Wорлд Сциентифиц. стр. 87—122. ИСБН 978-981-256-652-2. дои:10.1142/9789812708441_0006. Приступљено 7. 7. 2022.

[12] Нарици, Лаwренце; Бецкенстеин, Едwард (1997). „Тхе Хахн–Банацх Тхеорем: Тхе Лифе анд Тимес”. Топологy анд Итс Апплицатионс. 77 (2): 193—211. дои:10.1016/с0166-8641(96)00142-3.

[13] Лассак, M. (1993). „Аппроxиматион оф цонвеx бодиес бy рецтанглес”. Геометриае Дедицата. 47: 111—117. С2ЦИД 119508642. дои:10.1007/БФ01263495.

[:0-14] а ^б Санталó, L. (1961). „Собре лос системас цомплетос де десигуалдадес ентре трес елементос де уна фигура цонвеxа планас”. Матхематицае Нотае. 17: 82—104.

[:1-15] а ^б ^в Бранденберг, Ренé; Гонзáлез Мерино, Бернардо (2017). „А цомплете 3-дименсионал Бласцхке-Санталó диаграм”. Матхематицал Инеqуалитиес & Апплицатионс (на језику: енглески) (2): 301—348. ИССН 1331-4343. арXив:1404.6808 . дои:10.7153/миа-20-22 .

[16] Клее, Вицтор (1971), „Схапес оф тхе футуре”, Тхе Тwо-Yеар Цоллеге Матхематицс Јоурнал, 2 (2): 14—27, ЈСТОР 3026963, дои:10.2307/3026963 .

[icons-17] Алсина, Цлауди; Нелсен, Рогер Б. (2011), Ицонс оф Матхематицс: Ан Еxплоратион оф Тwентy Кеy Имагес, Долциани Матхематицал Еxпоситионс, 45, Матхематицал Ассоциатион оф Америца, п. 155, ИСБН 978-0-88385-352-8 .

[18] Моон, Ф. C. (2007), Тхе Мацхинес оф Леонардо Да Винци анд Франз Реулеауx: Кинематицс оф Мацхинес фром тхе Ренаиссанце то тхе 20тх Центурy, Хисторy оф Мецханисм анд Мацхине Сциенце, 2, Спрингер, ИСБН 978-1-4020-5598-0 .

[19] Тхе емптy сет ис импортант ин Минкоwски аддитион, бецаусе тхе емптy сет аннихилатес еверy отхер субсет: Фор еверy субсет $С$ оф а вецтор спаце, итс сум wитх тхе емптy сет ис емптy: $S+\emptyset =\emptyset$ .

[20] Тхеорем 3 (пагес 562–563): Креин, M.; Шмулиан, V. (1940). „Он регуларлy цонвеx сетс ин тхе спаце цоњугате то а Банацх спаце”. Анналс оф Матхематицс. Сецонд Сериес. 41 (3): 556—583. ЈСТОР 1968735. дои:10.2307/1968735.

[Schneider-21] Фор тхе цоммутативитy оф Минкоwски аддитион анд цонвеxифицатион, сее Тхеорем 1.1.2 (пагес 2–3) ин Сцхнеидер; тхис референце дисцуссес муцх оф тхе литературе он тхе цонвеx хуллс оф Минкоwски сумсетс ин итс "Цхаптер 3 Минкоwски аддитион" (пагес 126–196): Сцхнеидер, Ролф (1993). Цонвеx бодиес: Тхе Брунн–Минкоwски тхеорy. Енцyцлопедиа оф матхематицс анд итс апплицатионс. 44. Цамбридге: Цамбридге Университy Пресс. стр. xив+490. ИСБН 0-521-35220-7. МР 1216521.

[22] Лемма 5.3: Алипрантис, C.D.; Бордер, К.C. (2006). Инфините Дименсионал Аналyсис, А Хитцххикер'с Гуиде. Берлин: Спрингер. ИСБН 978-3-540-29587-7.

[Zalinescu_p._7-23] Зăлинесцу, C. (2002). Цонвеx аналyсис ин генерал вецтор спацес. Ривер Едге, Њ: Wорлд Сциентифиц Публисхинг Цо., Инц. стр. 7. ИСБН 981-238-067-1. МР 1921556.

[24] Раwлинс Г.Ј.Е. анд Wоод D, "Ортхо-цонвеxитy анд итс генерализатионс", ин: Цомпутатионал Морпхологy, 137-152. Елсевиер, 1988.

[25] Мункрес, Јамес; Топологy, Прентице Халл; 2нд едитион (Децембер 28, 1999). ISBN 0-13-181629-2.

[vanDeVel-26] ван Де Вел, Марцел L. Ј. (1993). Тхеорy оф цонвеx струцтурес. Нортх-Холланд Матхематицал Либрарy. Амстердам: Нортх-Холланд Публисхинг Цо. стр. xви+540. ИСБН 0-444-81505-8. МР 1234493.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]