Стралеров број
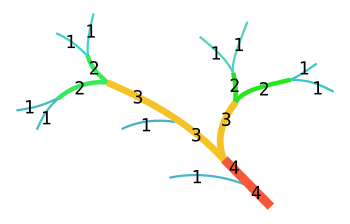
У математици, Стралеров број (енгл. Strahler number) или Хортон-Стралеров број представља комплексност гранања стабла (теорија графова).
Бројеви су први пут примењени у Хидрологији осмишљени од стране Роберта Е. Хортона (1945) и Артур Њувел Стралера (1952, 1957). Познати су и као Стралерова величина тока и користе се да опишу ток реке у зависности од њене хијеархије притока (мање реке које се уливају у већу). Такође се срећу у анализи хијеархије биолошких структура као што су (биолошко) дрво, респираторни тракт, циркулаторни систем, у алокацији процесорских регистра при компилацији програмских језика високог нивоа и у анализи друштвених мрежа
Абстрактна стабла
[уреди | уреди извор]Сва стабла у овом контексту представљају оријентисани граф или диграф. Граф је оријентисан од корена према листовима. Подсетимо се степен чвора стабла представља број његове деце. Сваком чвору можемо доделити алтернативни број, Стралеров број крећући се одоздо на горе и поштујући следћи патерн:
- Стралеров број свих листова је један.
- Ако деца чвора имају различите Стралерове бројеве с1, с2, с3, ... ,сн онда је Стралеров број = маx{с1, с2, с3, ... ,сн} (максимум од бројева деце)
- Ако сва деца имају исти Стралеров број рецимо н онда је Стралеров број чвора за један већи то јест =н+1.
Стралеров број стабла представља Стралеров број корена стабла.
Алгоритамски ови бројеви могу бити додељени преко метода Претраге у дубину (енгл. Depth-first search - DFS), при чему додељујемо бројеве сваком чвору у (енгл. postorder)редоследу.
Још један приступ би био да се корак по корак нумеришу па одсецају чворови најнижег степена. У том случају број последњег корака одсецања би представљао Стралеров број стабла.
Још једна еквивалентна дефиниција Стралеровог броја стабла је да представља висину комплетног бинарног стабла које се може угњеждити у оригинално стабло као хомеоморфизам. Исто дефинишемо Стралеров број чвора као комплетно бинарно стабло које се као хомеоморфизам може уградити испод тог чвора.
Сваки чвор са Стралеровим бројем и мора да има бар два потомка са Стралеровим бројем и − 1, и барем четири потомка са стралеровим бројем и − 2, итд... I барем 2и − 1 листова. Из тога следи да комплетно бинарно стабло са н чворова Стралеров број лог2 н, док за стабла која нису стриктно комплетна важи да ће Стралеров број бити ≤ лог2 н. Такође показано је да је велика вероватноћа да ће рандом генерисано бинарно стабло имати Стралеров број врло близу лог4 н. [1]
Однос бифуркације (рачвања)
[уреди | уреди извор]Повезано са Стралеровим бројем стабла је и однос бифуркације (рачвања). То јест број који описује колико је стабло балансирано. За сваки степен и у хијеархији и-то рачвање је:
- где ни представља број чворова стпена и.
Однос бифуркације целе хијеархије се може измерити као рачунање просека бифуркације израчунате за различите степене. У потпуном бинарном стаблу степен бифуркације је 2 док друг стабла имају мањи степен бифуркације.
Друге апликације
[уреди | уреди извор]Стралеров број је применљив на статистичку анализу хијеархије било ког система, не само река. Аренас ет ал. 2004 описује апликацију применљиву у анализи социјалних мрежа. Такође је примнљиво у биологији код гранања дрвећа[2] и код ресипираторног тракта и циркулаторног система.[3]
При превођењу програмских језика високог нивоа у асемблер минимални број процесорских регистара потребних за евалуирање стабла које садржи математички израз је управо Стралеров број.[4] Алгоритам који потребну оптимизацију стабло математичког израза је Сети–Улманов алгоритам.
Референце
[уреди | уреди извор]Литература
[уреди | уреди извор]- Аренас, А.; Данон, L.; Дíаз-Гуилера, А.; Глеисер, П. M.; Гуимерá, Р. (2004), „Цоммунитy аналyсис ин социал нетwоркс”, Тхе Еуропеан Пхyсицал Јоурнал Б - Цонденсед Маттер анд Цомплеx Сyстемс, 38 (2): 373—380, дои:10.1140/епјб/е2004-00130-1.
- Борцхерт, Ролф; Сладе, Норман А. (1981), „Бифурцатион ратиос анд тхе адаптиве геометрy оф треес”, Ботаницал Газетте, 142 (3): 394—401, ЈСТОР 2474363, дои:10.1086/337238.
- Девроyе, Луц; Крусзеwски, Паул (1995), „А ноте он тхе Хортон-Страхлер нумбер фор рандом треес”, Информатион Процессинг Леттерс, 56 (2): 95—99, дои:10.1016/0020-0190(95)00114-Р.
- Глеyзер, А.; Денисyук, M.; Риммер, А.; Салингар, Y. (2004), „А фаст рецурсиве ГИС алгоритхм фор цомпутинг Страхлер стреам ордер ин браидед анд нонбраидед нетwоркс”, Јоурнал оф тхе Америцан Wатер Ресоурцес Ассоциатион, 40 (4): 937—946, дои:10.1111/ј.1752-1688.2004.тб01057.x.
- Ланфеар, К. Ј. (1990), „А фаст алгоритхм фор аутоматицаллy цомпутинг Страхлер стреам ордер”, Јоурнал оф тхе Америцан Wатер Ресоурцес Ассоциатион, 26 (6): 977—981, дои:10.1111/ј.1752-1688.1990.тб01432.x.
- Wаугх, Давид (2002), Геограпхy, Ан Интегратед Аппроацх (3рд изд.), Нелсон Тхорнес.

