Alijasing
Ovaj članak možda zahteva čišćenje i/ili prerađivanje kako bi se zadovoljili standardi kvaliteta Vikipedije. Problem: jer mnogi strani izrazi stoje neprevedeni. |


U obradi signala i srodnih disciplina, alijasing je efekat koji čini da različiti signali da budu isti tokom diskretizovanja signala. Takođe se odnosi na izobličenje ili grešku koja proističe kada se signal rekonstruiše iz uzoraka koji se razlikuju od originalnog kontinuiranog signala.
Alijasing se može javiti u signalima uzorkovanih na vreme, na primer digitalni audio, i naziva se vremenski alijasing. Alijasing može doći i iz prostorno uzorkovanih signala, na primer digitalne slike. Alijasing iz prostorno uzorkovanih signala se zove prostorni alijasing.
Opis
[uredi | uredi izvor]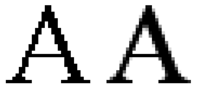
Kada se digitalna slika posmatra, rekonstrukcija se obavlja preko displeja ili štampača uređaja, kao i uz pomoć očiju i mozga. Ako podaci slika nisu pravilno obrađeni tokom uzorkovanja ili rekonstrukcije, rekonstruisana slika će se razlikovati od originalne slike, i alias se vidi.
Primer prostornog alijasinga je moare obrazac koji se može primetiti u slabo pikseliziranu sliku zida. Prostornim tehnikama anti-alijasing-a bi se izbegle ovakve jadne pikselizacije. Alijasing može biti uzrokovan bilo od uzrkovanja faze ili faze rekonstrukcije; oni mogu da se razlikuju pozivom za uzorkovanje preklapanja prealijasing-a i rekonstrukcije preklapanja postalijasing-a.[1]
Vremenski alijasing je glavni problem u uzorkovanju video i audio signala. Muzika, na primer, može da sadrži visoke frekvencije komponenti koje su nečujne ljudima. Ako komad muzike uzorkovane na 32000 uzoraka u sekundi (Hz), bilo koja frekvencija komponente iznad 16000 Hz (Nikvistove frekvencije) će izazvati alijasing kad muziku reprodukuje digitalno analogni konvertor (DAK). Da bi se sprečila ova anti-preklapanja koristi se filter za uklanjanje komponenti iznad Nikvistove frekvencije pre uzorkovanja.
U videima ili kinematografiji, vremenski alijasing je rezultat po stopi ograničenog okvira, i izaziva efekat karavan-točka, pri čemu se točak rotirati presporo ili čak unazad. Alijasing je promenio svoju prividnu učestalost rotacije. Ukidanje pravca može se opisati kao negativna frekvencija. Frekvencije vremenskog alijasing-a u videima i kinematografiji se određuje fremovima fotoaparata, ali relativni intenzitet aliased frekvencija je određena preko vremena zatvarača (vreme ekspozicije) ili upotrebom vremenskog filtera za smanjenje alijasing-a tokom snimanja.[2]
Kao i video kamere, većina šema uzorkovanja su periodične; to jest, imaju karakterističnu frekvenciju uzorkovanja u vremenu ili svemiru. Digitalni fotoaparati pružaju određeni broj uzoraka (pikseli) po stepenu ili po radianima, ili uzorci po mm u ravni fokusa kamere. Audio signali su uzrokovani (digitalizovani) sa analogno digitalnim konvertorom, koji proizvodi konstantan broj uzoraka u sekundi. Neki od najdramatičnijih i suptilnih primera alijasing-a javlja se kada se signal koji se uzorkuje ima periodičan sadržaj.
Bandlimited funkcije
[uredi | uredi izvor]Stvarni signali imaju konačno trajanje i njihov sadržaj frekvencija, kako je definisano Furijeovom transformacijom, nema gornje granice. Neka količina alijasing-a uvek dolazi kada se uzrokuju takve funkcije. Funkcije koje su sadržane u frekvenciji su ograničena (bandlimited) i imaju beskrajno trajanje. Ako su uzrokovane na dovoljno visokoj stopi, određivanje potpuno originalnih funkcija može u teoriji biti potpuno rekonstruisano iz beskonačnog skupa uzoraka.
Bandpass signali
[uredi | uredi izvor]Ponekad alijasing se namerno koristi za signale koji nemaju niske frekvencije sadržaja, pod nazivom pojasni signali. Undersampling, što stvara niske frekvencije pseudonime, može da proizvede isti rezultat, sa manje napora, kao učestalost menjanja-signala na nižim frekvencijama pre uzorkovanja na nižoj stopi. Neki digitalni channelizers[3] aliasinzi se mogu iskoristiti na ovaj način za računarsku efikasnost. Pogledajte uzorkovanja (obrada signala), Nikvistova stopa (odnos uzorkovanja), i Filter banku.
Uzorci sinusoidne funkcije
[uredi | uredi izvor]Sinusoide su važan tip periodične funkcije, jer realni signali su često modelovani kao sume mnogih sinusoida različitih frekvencija i različitih amplituda (kao, na primer, Furijeov red ili transformišu). Razumevanje šta alijasing radi na pojedinačne sinusoide je korisno u razumevanju šta se dešava njihovom zbiru.

Evo, zaplet prikazuje skup uzoraka čiji uzorak interval je 1, i dva (od mnogih) različita sinusoida koji su proizveli uzorke. Uzorak-stopa u ovom slučaju je fs=1. Na primer, ako je interval 1 sekunda, stopa je 1 uzorak po sekundi. Devet ciklusa crvenog sinusoida i 1 ciklus plavog sinusoida predstavljaju raspon intervala od 10 uzoraka. Odgovarajući broj ciklusa po uzorku su fred=0.9 i fblue=0.1. Ako su ovi uzorci proizvedeni od strane uzorkovanja funkcije cos(2π (0.9) X-θ) cos(2π i (0,1) k-φ), oni su takođe proizvedeni od strane trigonometričkih identičnih funkcijama, jer (2π (-0.9) k + θ) i cos(2π (-0.1) k + φ) uvodi koristan koncept negative frekvencije.
U principu, kada je sinusoida frekvencije f uzorkovana sa frekventnim fs može se razlikovati od onog drugog sinusoida čija se normalizovana frekvencija razlikuje od f/fs bio on ceo broj (pozitivnom ili negativnom)[note 1] . Zamena negativne frekvencije sinusoida svojom ekvivalentnom pozitivnom frekvencijom, možemo izraziti sve pseudonime frekvencija f kao falias(N)def= |f - N fs| za bilo koji ceo broj N, sa falias(0) = f budući da je stvarna vrednost, i N ima jedinice ciklusa po uzorku. Zatim N = 1 alias fred je fblue (i obrnuto).
Alijasing je važan kada pokušava da se rekonstruiše originalni oblik talasa od njenih uzoraka. Najčešća tehnika rekonstrukcije proizvodi najmanja od falias(N) frekvencija. Dakle, zato je obično važno da falias(0) bude jedinstvena minimalna vrednost. Neophodan je i dovoljan uslov za to fs/2 >|f| gde fs/2, obično se naziva Nikvistova frekvencija sistema čiji su uzorci po stopi fs. U našem primeru, stanje Nikvistove frekvencije je zadovoljno ako je originalni signal plava sinusoida (f = fblue). Ali ako je f = fred = 0.9, metod obične rekonstrukcije će proizvesti plavu sinusoid umesto crvene.

Sklapanje
[uredi | uredi izvor]U gornjem primeru, fred i fblue su simetrične oko frekvencija fs/2. I uopšte, kako se f povećava od 0 do fs/2, falias(1) se smanjuje iz fs do fs/2. Slično, kao kad f raste iz fs/2 u fs, falias(1) nastavlja da opada iz fs/2 do 0.
Grafikon amplitude i frekvencije za jednu sinusoidu na frekvenciji 0.6 fs i neke od svojih alijasa na 0.4 fs, 1.4 fs i 1.6 fs će izgledati kao 4 crne tačake na slici pored. Crvene linije prikazuju puteve (loci) od 4 tačke kada podesite frekvenciju i amplitudu sinusoide duž čvrstog crvenog segmenta (između fs/2 i fs). Bez obzira koju funkciju birate da promenite amplitude i frekvencije, grafik će izlagati simetriju između 0 i fs. Ova simetrija se najčešće naziva simetrija savijanja, i drugo ime za fs/2(Nikuistova frekvencije) je frekvencija savijanja. Sklapanje je najčešće primenjeno u praksi kada gledate frekvencijski spektar realnih-vrednih uzoraka koristeći diskretnu Fourier-ovu transformaciju.

Kompleks sinusoida
[uredi | uredi izvor]Složeni sinusoidi su talasastih oblika čiji uzorci su kompleksni brojevi, a koncept negativne frekvencije potrebno je razlikovati. U tom slučaju, frekvencije alijasa su date samo: falias(N) = f - Nfs, dakle, kako se f povećava iz fs/2 u fs falias(1) ide od -fs/2, do 0. Shodno tome, složeni sinusoidi ne pokazuju sklapanje. Složeni uzorci pravih vrednosti-sinusoida imaju nule-vrednosti imaginarne delove i pokazuju sklapanje.
Uzorak frekvencije
[uredi | uredi izvor]Kada se uslov fs/2 >f sretne na najvišoj frekvenciji komponento originalnog signala, onda se upozna sa svim frekvencijama komponenti. To stanje je poznato kao Nikvistov kriterijum. To se tipično aproksimira filtriranjem originalnog signala da se ublaže visoke frekvencije komponente pre nego što se uzrokuju. Ove oslabljene visoke frekvencije komponente i dalje generišu niske frekvencije pseudonime, ali obično u dovoljno malim amplituda da ne izazivaju probleme. Filter izabran u očekivanju nekog uzorka frekvencije se naziva anti-alijasing filter.

Signal filtrira se naknadno rekonstruiše, interpolacijom algoritama, bez značajnog dodatnog izobličenja. Većina uzrokovanih signala se ne samo čuva i nego i obnovlja. Ali vernost iz teorijske rekonstrukcije (preko Vitaker-Šenon interpolacione formule ) predstavlja uobičajenu meru efikasnosti uzrokovanja.
Istorijska upotreba
[uredi | uredi izvor]Istorijski termin alijasing evoluirao je od radio tehnike, zbog delovanja superheterodinog prijemnika. Kada prijemnik pomera više signala na niže frekvencije, iz RF u IF od heterodyning, neželjeni signal iz RF frekvencije podjednako je daleko od lokalnog oscilatora (LO) frekvencije kao željenog signala, ali na pogrešnoj strani LO, može završiti na istoj ako frekvencija željeni jedan. Ako je dovoljno jaka da može da ometa prijem željenog signala. Ovaj neželjeni signal poznat je kao slika ili alias željenog signala.
Ugaoni alijasing
[uredi | uredi izvor]Alijasing se javlja svaki put kada je upotreba diskretnih elemenata za snimanje ili proizvedeni kontinuirani signalni uzroci frekvencije su dvosmisleni.
Prostorni alijasing, posebno ugaone frekvencije, može da dođe kada se reprodukuje svetlosno polje[4] ili zvučno polje sa diskretnim elementima, kao iu 3D ekranima ili sinteza talasa polja zvuka.
Ovaj alijasing je vidljiv u slikama, kao što su posteri lentikularne štampe: ako imaju niske ugaone rezolucije, onda se jedan kreće pored njih, kažu sleva nadesno, 2D slika se u početku menja (tako da izgleda da se levo kreće) , onda kao jedan kreće na sledeću ugaonu sliku, slika se iznenada menja (tako da skače) - i učestalost i amplituda ove strane-na-strani pokreta odgovara ugaonoj rezoluciji slike (i za frekvencije, brzina bočnog pomeranja posmatrača), koja je ugaoni alijasing na 4D svetlosnom terenu.
Nedostatak paralaksa o kretanju gledaoca u 2D slikama i [3D filmovima] u produkciji stereoskopskih naočara (u 3D filmovima efekat se zove "menjanje nagiba", jer slika izgleda da rotira oko svoje ose) na sličan način može se posmatrati kao gubitak ugaone rezolucije, sve ugaone frekvencije aliased-a do 0 (konstanta).
Još primera
[uredi | uredi izvor]Onlajn audio primer
[uredi | uredi izvor]Kvalitativni efekti alijasing-a se mogu čuti u sledećoj audio demonstraciji. Šest sawtooth talasa se igra u nizu, prva dva sawtooth talasa imaju fundamentalnu frekvenciju od 440 Hz (A4), druga dva imaju fundamentalnu frekvenciju od 880 Hz (A5), a preostala dva na 1760 Hz(A6). Ѕawtooth alternativa bandlimited (ne-aliased) sawtooth i aliased sawtooth i uzorkovanja je 22.05 kHz. U bandlimited-u sawtooth se sintetiše i sawtooth talasi Furijeove serije tako da je harmonija iznad Nikuistove frekvencije prisutna.
Alijasing distorzija na nižim frekvencijama je sve očiglednija sa višim frekvencijama, i dok je bandlimited sawtooth još uvek jasno na 1760 Hz, aliased ѕawtooth je degradiran i oštro sa zujanjem se čuje na frekvencijama nižim od osnovnih.
Određivanje pravaca
[uredi | uredi izvor]Oblik prostornog alijasinga može doći iz antenskih nizova ili mikrofonskih nizova koji se koriste za procenu smera dolaska signala talasa, kao i geofizička istraživanja od seizmičkih talasa. Talasi moraju da se uzrokuju u više od dve tačke na talasnoj dužini ili pravac talasa koji dolazi postaje nejasna.[5]
Napomene
[uredi | uredi izvor]- ^ Adding an integer number of cycles between the samples of a sinusoid has no effect on the values at the sample points. That is the essence of aliasing.
Reference
[uredi | uredi izvor]- ^ Mitchell, Don P.; Netravali, Arun N. (1988). „Reconstruction filters in computer-graphics”. Proceedings of the 15th annual conference on Computer graphics and interactive techniques - SIGGRAPH '88. str. 221–228. ISBN 0897912756. S2CID 1630378. doi:10.1145/54852.378514.
- ^ Tessive, LLC (2010)."Time Filter Technical Explanation"
- ^ Harris 2006.
- ^ The (New) Stanford Light Field Archive
- ^ Flanagan J.L, ‘Beamwidth and useable bandwidth of delay- steered microphone arrays’, AT&T Tech. J, 1985, 64. str. 983–995
Literatura
[uredi | uredi izvor]- Mitchell, Don P.; Netravali, Arun N. (1988). „Reconstruction filters in computer-graphics”. Proceedings of the 15th annual conference on Computer graphics and interactive techniques - SIGGRAPH '88. str. 221–228. ISBN 0897912756. S2CID 1630378. doi:10.1145/54852.378514.
- Harris, Frederic J. (2006). Multirate Signal Processing for Communication Systems. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-146511-4.
- Pharr, Matt; Humphreys, Greg (2010). Physically Based Rendering: From Theory to Implementation. Morgan Kaufmann. ISBN 978-0-12-375079-2. Pristupljeno 3. 3. 2013.
Spoljašnje veze
[uredi | uredi izvor]- Aliasing by a sampling oscilloscope na sajtu YouTube by Tektronix Application Engineer
- Anti-Aliasing Filter Primer by La Vida Leica discusses its purpose and effect on the image recorded.
- Frequency Aliasing Demonstration by Burton MacKenZie using stop frame animation and a clock.
- Interactive examples demonstrating the aliasing effect

