Apsolutna zvezdana veličina
Apsolutna zvezdana veličina (M) (ili magnituda, od latinskog magnitudo) predstavlja prividnu zvezdanu veličinu nebeskog tela u slučaju kada bi se ono nalazilo na rastojanju od 10 parseka. Ovakva definicija se koristi za objekte u našoj Galaksiji i tela van Mlečnog puta, dok za tela u Sunčevom sistemu se koristi druga referentna udaljenost i meri se sjaj kakav bi telo imalo na udaljenosti od 1 AJ.
Kao i kod svih astronomskih magnituda, apsolutna magnituda se može specificirati za različite opsege talasnih dužina koji odgovaraju specificiranim filterskim opsezima ili propusnim opsegima; za zvezde uobičajena apsolutna magnituda je apsolutna vizuelna veličina, koja koristi vizuelni opseg spektra (u UBV fotometrijskom sistemu). Apsolutne veličine su označene velikim M, sa indeksom koji predstavlja filterski opseg koji se koristi za merenje, kao što je MV za apsolutnu magnitudu u vizuelnom opsegu.
Što je objekat svetliji, to je manja numerička vrednost njegove apsolutne veličine. Razlika od 5 magnituda između apsolutnih veličina dva objekta odgovara odnosu od 100 u njihovim luminoznostima, a razlika od n magnitude u apsolutnoj veličini odgovara odnosu osvetljenosti od 100n/5 Na primer, zvezda apsolutne magnitude MV=3,0 bi bila 100 puta svetlija od zvezde apsolutne magnitude MV=8,0 mereno u vidljivom filterskom opsegu. Sunce ima apsolutnu magnitudu MV=+4,83.[1] Jako luminozni objekti mogu imati negativne apsolutne magnitude: na primer, galaksija Mlečni put ima apsolutnu vidljivu magnitudu od oko -20,8.[2]
Apsolutna bolometrijska magnituda objekta (Mbol) predstavlja njegovu ukupnu luminoznost na svim talasnim dužinama, a ne u jednom filterskom opsegu, kao što je izraženo na logaritamskoj skali magnituda. Za konvertovanje iz apsolutne veličine u određenom opsegu filtera u apsolutnu bolometrijsku magnitudu, primenjuje se bolometrijska korekcija (BC).[3]
Veza sa prividnom zvezdanom veličinom
[uredi | uredi izvor]Kako se zvezde nalaze na različitim udaljenostima od Zemlje, prividna zvezdana veličina nam nije od koristi pri poređenju ukupnog intenziteta sjaja neke dve zvezde ukoliko se nalaze na različitim udaljenostima, što jeste najčešći slučaj. Zbog toga se uvodi apsolutna zvezdana veličina (M). Veza između apsolutne i prividne zvezdane veličine data je formulom:
gde je r udaljenost tela od Zemlje izražena u parsecima, a log logaritam sa osnovom 10. Data formula se može predstaviti i kao:
gde je godišnja paralaksa zvezde izražena u uglovnim sekundama. Pri tome koristimo jednakost:
Veza sa površinskim sjajem
[uredi | uredi izvor]Kada smo odredili apsolutne zvezdane veličine dve zvezde i time ih doveli na isto rastojanje od Zemlje možemo povezati osećaj nadražaja detektora svetlosti (koji predstavlja apsolutna zvezdana veličina) i objektivnu fizičku veličinu luminoznost (L) koristeći se formulom:
Apsolutna zvezdana veličina nekih tela
[uredi | uredi izvor]Apsolutna zvezdana veličina Sunca iznosi +4.m8, zvezde Sirijus +1.m5, a zvezde Alfa Kentaur +4.m3.
Tela Sunčevog sistema (H)
[uredi | uredi izvor]| H | Dijametar |
|---|---|
| 10 | 34 km |
| 12,6 | 10 km |
| 15 | 3.4 km |
| 17,6 | 1 km |
| 19,2 | 500 metar |
| 20 | 340 metar |
| 22,6 | 100 metar |
| 24,2 | 50 metar |
| 25 | 34 metar |
| 27,6 | 10 metar |
| 30 | 3,4 metar |
Za planete i asteroide koristi se definicija apsolutne veličine koja je značajnija za nezvezdane objekte. Apsolutna magnituda, koja se obično naziva , definiše se kao prividna veličina koju bi objekat imao da je na udaljenosti od jedne astronomske jedinice (AJ) od Sunca i od posmatrača, i u uslovima idealne solarne opozicije (aranžman koji je u praksi nemoguć).[5] Tela Sunčevog sistema su osvetljena Suncem, tako da njihova svetlost varira u zavisnosti od uslova osvetljenja, opisanih faznim uglom. Ovaj odnos se naziva fazna kriva. Apsolutna magnituda je osvetljenost pri nultom faznom uglu, rasporedu poznatom kao opozicija, sa udaljenosti od jedne AJ.
Prividna zvezdana veličina
[uredi | uredi izvor]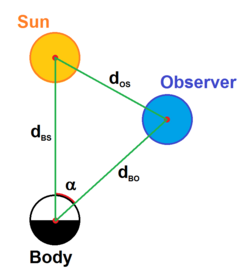
Apsolutna magnitude se može koristiti za izračunavanje prividne veličine tela. Za objekat koji reflektuje sunčevu svetlost, i su povezani relacijom
gde je fazni ugao, ugao između linija telo-Sunce i telo-posmatrač. je fazni integral (integracije reflektovane svetlosti; broj u opsegu od 0 do 1).[6]
Po kosinusnoj teoremi se može napisati:
Rastojanja:
- dBO je rastojanje između tela i posmatrača
- dBS je rastojanje između tela i Sunca
- dOS je rastojanje između posmatrača i Sunca
- d0 je 1 AJ, prosečna udaljenost između Zemlje i Sunca.
Aproksimacije za fazni integral
[uredi | uredi izvor]Vrednost zavisi od svojstava reflektujuće površine, posebno od njene hrapavosti. U praksi se koriste različite aproksimacije na osnovu poznatih ili pretpostavljenih osobina površine.[6]
Planete kao difuzne sfere
[uredi | uredi izvor]

Planetarna tela se mogu dosta dobro aproksimirati kao idealne difuzne reflektujuće sfere. Neka je fazni ugao u stepenima, onda[7]
Difuzna sfera pune faze reflektuje dve trećine svetlosti kao difuzni ravan disk istog prečnika. Četvrtina faze () ima toliko svetlosti koliko i puna faza ().
Nasuprot tome, model reflektora difuznog diska je jednostavno , što nije realno, ali predstavlja opozicioni efekat za grube površine koje reflektuju ravnomerniju svetlost nazad pri niskim faznim uglovima.
Definicija geometrijskog albeda , mera za reflektivnost planetarnih površina, zasnovana je na modelu reflektora difuznog diska. Apsolutna magnituda , prečnik (u kilometrima) i geometrijski albedo tela su povezani izrazom[8][9][10]
- km.
Primer: Mesečeva apsolutna magnituda se može izračunati iz njegovog prečnika i geometrijskog albeda :[11]
Dobija se , U četvrtini faze, (prema modelu difuznog reflektora), ovo daje prividnu magnitudu od Stvarna vrednost je nešto niža od nje, Fazna kriva Meseca je previše komplikovana za model difuznog reflektora.[12]
Napredniji modeli
[uredi | uredi izvor]Pošto tela Sunčevog sistema nikada nisu savršeni difuzni reflektori, astronomi koriste različite modele da predvide prividne magnitude na osnovu poznatih ili pretpostavljenih osobina tela.[6] Za planete, aproksimacije za termin korekcije u formuli za m su izvedene empirijski, da bi se uskladila zapažanja pod različitim faznim uglovima. Aproksimacije koje preporučuje Astronomski almanah[13] su (sa u stepenima):
| Planeta | Aproksimacija za | |
|---|---|---|
| Merkur | −0,613 | |
| Menera | −4,384 |
|
| Zemlja | −3,99 | |
| Mars | −1,601 |
|
| Jupiter | −9,395 |
|
| Saturn | −8,914 |
|
| Uran | −7,110 | (za ) |
| Neptun | −7,00 | (za i ) |
Ovde je efektivni nagib Saturnovih prstenova (njihov nagib u odnosu na posmatrača), koji, gledano sa Zemlje, varira između 0° i 27° tokom jedne Saturnove orbite, i je mali korekconi član u zavisnosti od Uranove podzemlje i sub-solarne geografske širine. je godina sadašnje ere. Apsolutna magnituda Neptuna se sporo menja zbog sezonskih efekata kako se planeta kreće duž svoje 165-godišnje orbite oko Sunca, a gornja aproksimacija važi tek posle 2000. godine. Za neke okolnosti, kao što je za Veneru, nema dostupnih zapažanja, i fazna kriva je nepoznata u tim slučajevima.
Primer: 1. januara 2019. Venera je bila od Sunca i od Zemlje, pod faznim uglom od (blizu četvrtine faze). U uslovima pune faze, Venera bi bila vidljiva na Uzimajući u obzir veliki fazni ugao, gornji termin korekcije daje stvarnu prividnu magnitudu od Ovo je blizu vrednosti od koju je predvidela Laboratorija za mlazni pogon.[14]
Zemljin albedo varira za faktor 6, od 0,12 u slučaju bez oblaka do 0,76 u slučaju oblaka altostratusa. Apsolutna magnituda ovde odgovara albedu od 0,434. Prividna magnituda Zemlje ne može se predvideti tako tačno kao kod većine drugih planeta.[13]
Vidi još
[uredi | uredi izvor]Reference
[uredi | uredi izvor]- ^ „Sun Fact Sheet”. NASA Goddard Space Flight Center. Pristupljeno 25. 2. 2017.
- ^ Karachentsev, I. D.; et al. (2004). „A Catalog of Neighboring Galaxies”. The Astronomical Journal. 127 (4): 2031—2068. Bibcode:2004AJ....127.2031K. doi:10.1086/382905
 .
.
- ^ Flower, P. J. (septembar 1996). „Transformations from Theoretical Hertzsprung-Russell Diagrams to Color-Magnitude Diagrams: Effective Temperatures, B-V Colors, and Bolometric Corrections”. The Astrophysical Journal. 469: 355. Bibcode:1996ApJ...469..355F. doi:10.1086/177785.
- ^ CNEOS Asteroid Size Estimator
- ^ Luciuk, M., Astronomical Magnitudes (PDF), str. 8, Arhivirano iz originala (PDF) 20. 09. 2018. g., Pristupljeno 11. 1. 2019
- ^ a b v Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, K. J. (2016). Fundamental Astronomy. Springer. str. 163. ISBN 9783662530450.
- ^ Whitmell, C. T. (1907), „Brightness of a planet”, The Observatory, 30: 97, Bibcode:1907Obs....30...96W
- ^ Bruton, D., Conversion of Absolute Magnitude to Diameter for Minor Planets, Stephen F. Austin State University, Arhivirano iz originala 10. 12. 2008. g., Pristupljeno 12. 1. 2019
- ^ The factor for a diffuse disk reflector can be computed as , where , the absolute magnitude of the Sun, and
- ^ Chesley, Steven R.; Chodas, Paul W.; Milani, Andrea; Valsecchi, Giovanni B.; Yeomans, Donald K. (oktobar 2002). „Quantifying the Risk Posed by Potential Earth Impacts” (PDF). Icarus. 159 (2): 425. Bibcode:2002Icar..159..423C. doi:10.1006/icar.2002.6910. Arhivirano iz originala (PDF) 2003-11-04. g. Pristupljeno 15. 4. 2020.
- ^ Albedo of the Earth, Department of Physics and Astronomy, Pristupljeno 12. 1. 2019
- ^ Luciuk, M., Albedo – How bright is the Moon?, Pristupljeno 12. 1. 2019
- ^ a b Anthony, M.; Hilton, J. L. (oktobar 2018). „Computing apparent planetary magnitudes for The Astronomical Almanac”. Astronomy and Computing. 25: 10—24. Bibcode:2018A&C....25...10M. S2CID 69912809. arXiv:1808.01973
 . doi:10.1016/j.ascom.2018.08.002.
. doi:10.1016/j.ascom.2018.08.002.
- ^ JPL Horizons (Ephemeris Type "OBSERVER", Target Body "Venus [299]", Observer Location "Geocentric [500]", Time Span "Start=2019-01-01 00:00, Stop=2019-01-02 00:00, Step=1 d", QUANTITIES=9,19,20,24), Jet Propulsion Laboratory, Pristupljeno 11. 1. 2019
Spoljašnje veze
[uredi | uredi izvor]- Reference zero-magnitude fluxes Arhivirano 22 februar 2003 na sajtu Wayback Machine
- International Astronomical Union
- Absolute Magnitude of a Star calculator
- The Magnitude system
- About stellar magnitudes Arhivirano na veb-sajtu Wayback Machine (27. oktobar 2021)
- Obtain the magnitude of any star – SIMBAD
- Converting magnitude of minor planets to diameter
- Another table for converting asteroid magnitude to estimated diameter





































































