Globus

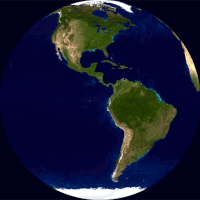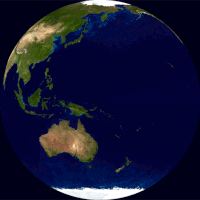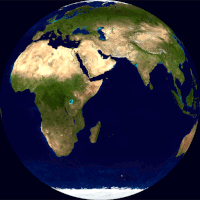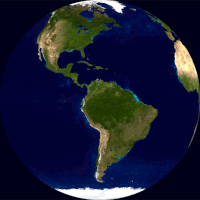
Globus (lat. globus — „lopta”) je umanjeni loptasti prikaz Zemlje, planeta ili nebeske sfere sa ucrtanim kartografskim prikazom date površine. Odnos i geometrijska podudarnost sa stvarnim prikazima je najsličnija od svih mogućih interpretacija (mapa i dr). Prema tipu globusi se mogu podeliti na geografske i astronomske.[1] U nastavi geografije, sferni prikaz Zemlje je jedan od osnovnih učila.
Globus prikazuje detalje svoje teme. Zemaljski globus prikazuje kopnene mase[2][3][4][5][6] i vodena tela.[7][8][9] On može da prikaže nacije i veće gradove i mrežu linija geografske širine i dužine.[10][11] Neki imaju podignuti reljef da bi prikazali planine i druge velike reljefne oblike. Nebeski globus prikazuje značajne zvezde, a može da prikazuje i položaje drugih istaknutih astronomskih objekata. Obično će takođe podeliti nebesku sferu na sazvežđa.
Zemaljski i planetarni
[uredi | uredi izvor]
Ravne karte se kreiraju korišćenjem projekcije karte koja neizbežno unosi sve veću količinu izobličenja što je veća površina koju mapa prikazuje.[12][13][14][15][16] Globus je jedini prikaz Zemlje koji ne iskrivljuje ni oblik ni veličinu velikih obeležja – kopnenih masa, vodenih površina itd.
Obim Zemlje je prilično blizu 40 miliona metara.[17][18] Mnogi globusi su napravljeni sa obimom od jednog metra, tako da su modeli Zemlje u razmeri 1:40 miliona. U imperijalnim jedinicama, mnogi globusi se prave sa prečnikom od jedne stope (oko 30 cm), što daje obim od 3,14 stopa (oko 96 cm) i razmeru od 1:42 miliona. Globusi se takođe prave u mnogim drugim veličinama.
Neki globusi imaju površinsku teksturu koja pokazuje topografiju ili batimetriju. U njima su uzvišenja i depresije namerno preuveličane, jer bi inače bile jedva vidljive. Na primer, jedan proizvođač proizvodi trodimenzionalni izdignuti reljefni globus prečnika 25 in (64 cm) (ekvivalentno obimu od 200 cm, ili približno skale od 1:20 miliona) koji prikazuje najviše planine preko 1 in (2,5 cm), što je oko 57 puta više od tačne skale Mont Everesta.[19][20]
Istorija
[uredi | uredi izvor]Prvi globusi pojavili su se još u starom veku, odmah po saznanju da je Zemlja okrugla. Prvim tvorcem smatra se Krates sa ostrva Malos, koji je u II veku pre nove ere izradio sferni model planete.[21] Klaudije Ptolemej je u svom delu „Geografija“, dao uputstva za izradu globusa. Tokom XIII veka u arapskom svetu je napravljenom nekoliko modela Zemlje, samo dva u sačuvana do danas. Martin Behajm je 1492. godine konstruisao prvi globus u srednjem veku, i to pre otkrića Novog sveta.
Osobine
[uredi | uredi izvor]Preslikavanje Zemljine površine na globus vrši se po pravilima centralne projekcije. Naime, zamisle se dve identične lopte sa zajedničih centrom, od kojih je Zemlja veća, a uzeta sfera manja. Zatim, se tačke projektuju zamišljenim zracima koji se sastaju u zajedničkom središtu. Time se projekcije površina sa Zemlje nalaze na globusu u tačkama presecanja. Razmer globusa je jednak u svakoj tački. Uglovi sa modela su jednaki istovetnim na Zemljinoj lopti, pa se to naziva konformnost. Takođe i odnos površina je u razmeri.
Glavna svojstva svakog globusa su: očuvanje sličnosti figure, konformnost uglova i ekvivalentnost površina i linija. Na osnovu ovih pokazatelja globus je naverniji i najpribližniji prikaz Zemljine lopte. Na loptu malog prečnika povlače se geografske koordinate (uporednici i podnevci), osovine koje povezuju severni i južni pol nagnu su za 23 stepena i 27 minuta i unese se geografski sadržaj. Izrađuju se modeli koji imaju približan oblik Zemlje da bi se izbegle sve deformacije. Na njemu ne postoje deformacije dužina u bilo kom pravcu, kao ni uglova bez obzira na pravac pružanja krakova. Zbog svega toga globus je veran prikaz Zemljine površine.[22]
Razmer globusa
[uredi | uredi izvor]Razmera je po pravilu mala. Najčešće se izrađuju sa prečnikom od 50 do 60cm. To je u stvari razmera od 1:25 000 000 do 1:21 000 000. Na toj razmeri razlika između Zemljinih poluosa ne prelazi dužinu od 1 mm. To je zanemarljiva razlika što omogućava da se globusi izrađuju kao lopte, a ne kao elipsoidi. Na međunarodnoj izložbi u Parizu 1889. godine izložen je model prečnika 12,5 m i težak oko deset tona u razmeri 1:1.000.000. Jedan od najmanjih globusa potiče iz 1507. godine i poznat je kao Jagelovski globus iz Krakova. Njegov prečnik je 7,3 cm.[22]
Podela
[uredi | uredi izvor]Globusi se mogu podeliti na više tipova.[1]
- geografske (opšti, tematski i indukcioni)
- astronomske (zvezdani, planetarni i mesečevi)
Galerija
[uredi | uredi izvor]-
Nebeski globus
-
Globusi
-
Behajmov globus
-
Replika starog francuskog globusa
Vidi još
[uredi | uredi izvor]Reference
[uredi | uredi izvor]- ^ a b Mastilo, Natalija (2005). Rečnik savremene srpske geografske terminologije. Beograd: Geografski fakultet Univerziteta u Beogradu. str. 58.
- ^ „Landmass”. Cambridge Dictionary. Cambridge.org Dictionary. Pristupljeno 17. 1. 2023.
- ^ „Landmass”. Merriam-Webster. Merriam-Webster.com Dictionary. Pristupljeno 17. 1. 2023.
- ^ Cook, Peter J.; Carleton, Chris M., ur. (9. 11. 2000). Continental Shelf Limits: The Scientific and Legal Interface. Oxford University Press. str. 298. ISBN 9780197561218. doi:10.1093/oso/9780195117820.001.0001 — preko Google Books.
- ^ Nijman, Jan; Muller, Peter O.; de Blij, H.J. (2017). „Introduction”. Regions: Geography: Realms, Regions, and Concepts (17th izd.). Wiley. str. 11. ISBN 978-1-119-30189-9.
- ^ „Landmass”. Dictionary.com. Dictionary.com, LLC. Pristupljeno 25. 7. 2020.
- ^ Langbein, W.B.; Iseri, Kathleen T. (1995). „Hydrologic Definitions: Stream”. Manual of Hydrology: Part 1. General Surface-Water Techniques (Water Supply Paper 1541-A). Reston, VA: USGS..
- ^ „What causes high tide and low tide? Why are there two tides each day?”. HowStuffWorks (na jeziku: engleski). 21. 5. 2009. Pristupljeno 10. 12. 2017.
- ^ „European Environment Agency's home page — European Environment Agency”. www.eea.europa.eu (na jeziku: engleski). Pristupljeno 2022-11-03.
- ^ Chang, Kang-tsung (2016). Introduction to Geographic Information Systems (9th izd.). McGraw-Hill. str. 24. ISBN 978-1-259-92964-9.
- ^ Taylor, Chuck. „Locating a Point On the Earth”. Arhivirano iz originala 3. 3. 2016. g. Pristupljeno 4. 3. 2014.
- ^ Lambert, Johann; Tobler, Waldo (2011). Notes and comments on the composition of terrestrial and celestial maps. Redlands, CA: ESRI Press. ISBN 978-1-58948-281-4.
- ^ Richardus, Peter; Adler, Ron (1972). map projections. New York, NY: American Elsevier Publishing Company, inc. ISBN 0-444-10362-7.
- ^ Robinson, Arthur; Randall, Sale; Morrison, Joel; Muehrcke, Phillip (1985). Elements of Cartography (fifth izd.). ISBN 0-471-09877-9.
- ^ Snyder, J.P.; Voxland, P.M. (1989). „An album of map projections”. Album of Map Projections (PDF). U.S. Geological Survey Professional Paper. 1453. United States Government Printing Office. doi:10.3133/pp1453. Pristupljeno 8. 3. 2022.
- ^ Ghaderpour, E. (2016). „Some equal-area, conformal and conventional map projections: a tutorial review”. Journal of Applied Geodesy. 10 (3): 197—209. Bibcode:2016JAGeo..10..197G. S2CID 124618009. arXiv:1412.7690
 . doi:10.1515/jag-2015-0033.
. doi:10.1515/jag-2015-0033.
- ^ The Earth’s circumference is 40 million m because the metre was originally defined to be one 10-millionth of the distance between the poles and the equator.
- ^ Arc length#Arcs of great circles on the Earth
- ^ MapScaping på Twitter: "3D topographic globe at Stanford's Branner Library."
- ^ The GEO One 25" Extreme Raised Relief Classroom Floor Globe
- ^ Lješević, Milutin; Živković, Dragica (2001). Kartografija. Beograd: Geografski fakultet Univerziteta u Beogradu. str. 25—34.
- ^ a b Ćurčić, Slobodan; Ristanović, Branko (2010). Kartografija. Novi Sad: Prirodno-matematički fakultet, Departman za geografiju, turizam i hotelijerstvo. str. 138—139.
Literatura
[uredi | uredi izvor]- Mastilo, N. (2005): Rečnik savremene srpske geografske terminologije, Geografski fakultet, Beograd; ISBN 978-86-82657-55-2
- Lješević, A. i Živković, D. (2001): Kartografija, Geografski fakultet, Beograd; ISBN 978-86-83501-06-9
- Oliver, Bernard M. (1972). „The Shape of the Analemma”. Sky and Telescope. 44: 20. Bibcode:1972S&T....44...20O.
- Kittler, Richard; Darula, Stan (2004). „Analemma, the Ancient Sketch of Fictitious Sunpath Geometry—Sun, Time and History of Mathematics”. Architectural Science Review. 47 (2): 141—4. S2CID 122005748. doi:10.1080/00038628.2004.9697037.
- Sidoli, Nathan (2005). „Heron's Dioptra 35 and Analemma Methods: An Astronomical Determination of the Distance between Two Cities”. Centaurus. 47 (3): 236—58. Bibcode:2005Cent...47..236S. doi:10.1111/j.1600-0498.2005.470304.x.
- Semazzi, Fredrick H.M.; Scroggs, Jeffrey S.; Pouliot, George A.; McKee-Burrows, Analemma Leia; Norman, Matthew; Poojary, Vikram; Tsai, Yu-Ming (2005). „On the Accuracy of Semi-Lagrangian Numerical Simulation of Internal Gravity Wave Motion in the Atmosphere”. Journal of the Meteorological Society of Japan. 83 (5): 851—69. doi:10.2151/jmsj.83.851
 .
. - Luckey, P. (1927). „Das Analemma von Ptolemäus” [The analemma by Ptolemy]. Astronomische Nachrichten (na jeziku: nemački). 230 (2): 17—46. Bibcode:1927AN....230...17L. doi:10.1002/asna.19272300202.
- Id, Yusif (decembar 1969). „An Analemma Construction for Right and Oblique Ascensions”. The Mathematics Teacher. 62 (8): 669—72. JSTOR 27958259. doi:10.5951/MT.62.8.0669.
- Yeow, Teo Shin (2002). The Analemma for Latitudinally-Challenged People (PDF) (BS Thesis). National University of Singapore. Arhivirano iz originala (PDF) 2011-05-17. g. Pristupljeno 2006-02-05.
- Encyclopædia Britannica (1771), "Geography".
- Darlington, Oscar G. "Gerbert, the Teacher," The American Historical Review (Volume 52, Number 3, 1947): 456–476.
- Kern, Ralf: Wissenschaftliche Instrumente in ihrer Zeit. Vom 15. – 19. Jahrhundert. Verlag der Buchhandlung Walther König 2010, ISBN 978-3-86560-772-0
- Needham, Joseph (1986). Science and Civilization in China: Volume 3. Taipei: Caves Books, Ltd.
- Sivin, Nathan (1995). Science in Ancient China. Brookfield, Vermont: VARIORUM, Ashgate Publishing
- Williams, Henry Smith (2004). A History Of Science. Whitefish, MT: Kessinger Publishing. ISBN 1-4191-0163-3.
- Borchert, Donald M. (2006). In Encyclopedia of Philosophy, 2nd ed. Macmillan Reference. str. 532—536.
- Dewald, Jonathan (2004). Encyclopedia of the Early Modern World. Charles Scribner's Sons. str. 148—154.
- Savage-Smith, Emily (1985). A History of Celestial Globes in the Greco-Roman and Islamic Worlds" in Islamicate Celestial Globes: Their History, Construction, and Use. Washington DC: Smithsonian Institution Press.
- Savage-Smith, Emilie (2013). God is beautiful and loves beauty: the object in Islamic art and culture. Yale University Press. str. 123—155.
- Carey, Moya (2009). „The Gold and Silver Lining: Shams Al-Dīn Muḥammad B. Mu'ayyad Al-'Urḍī's Inlaid Celestial Globe (C. Ad 1288) from the Ilkhanid Observatory at Marāgha”. Iran. 47: 97—108. JSTOR 25651466. S2CID 193493577. doi:10.1080/05786967.2009.11864761 — preko JSTOR.
- „Celestial globe”. National Museums Scotland (na jeziku: engleski). Pristupljeno 2020-10-15.
- Savage-Smith, Emilie (1985). Islamicate Celestial Globes: Their History, Construction, and Use. Washington, D.C.: Smithsonian Institution Press.
- „Using the EPSG geodetic parameter dataset, Guidance Note 7-1”. EPSG Geodetic Parameter Dataset. Geomatic Solutions. Arhivirano iz originala 15. 12. 2021. g. Pristupljeno 15. 12. 2021.
Spoljašnje veze
[uredi | uredi izvor]- Kratka istorija kartografije: Kako su naši preci mapirali svet (TV Istorija - Zvanični jutjub kanal)
- ppmglobe – generate strips to glue onto a sphere
- 3D VRML globe
- 3D Java Globe with coastlines, parallels, meridians, etc. Arhivirano na sajtu Wayback Machine (7. mart 2019)
- How to orient a globe in homothetic position to the Earth Arhivirano na sajtu Wayback Machine (28. januar 2020)
- Glossary to World Globe Terms Arhivirano na sajtu Wayback Machine (25. jun 2020)
- Behind the scenes at London's globe-making workshop – a photo essay (August 2017), The Guardian




