Kvadratni koren iz 3

	Spisak prirodnih brojeva \| Iracionalan broj ζ(3); √2; √3; √5; φ; e; π;
Binarni sistem	1.10111011011001111010…
Decimalni sistem	1.7320508075688772935…
Heksadecimalni sistem	1.BB67AE8584CAA73B…
Verižni razlomak

Kvadratni koren iz 3 je pozitivan realan broj koji, kada se množi sa sobom, daje broj 3 . Tačnije se naziva glavni kvadratni koren iz 3, da bi se razlikovao od negativnog broja sa istim svojstvom. Označen je sa √3 .

Kvadratni koren iz 3 je iracionalan broj . Poznat je i kao Teodorova konstanta, nazvana po Teodoru iz Cirene, koji je dokazao njegovu iracionalnost.

Prvih šezdeset cifara njegovog decimalnog proširenja su:

1.73205080756887729352744634150587236694280525381038062805580… (sekvenca A002194 u OEIS)

Od decembra 2013. godine, njena brojčana vrednost u decimalnim brojevima izračunata je na najmanje deset milijardi cifara. ^[1]

Razlomak 97/56 (7000173214285700000♠1,732142857 ...) za kvadratni koren od tri se može koristiti kao približna vrednost. Uprkos tome što ima imenilac od samo 56, razlikuje se od pravilne vrednosti za manje od 1/10,000 (približno 6995920000000000000♠9,2×10⁻⁵). Zaokružena vrednost od 1.732 je tačna do 0,01% od stvarne vrednosti.

Arhimed prijavio $(1351 / 780) 2 > 3 > (265 / 153) 2$ , ^[2] tačno do 1/608400 (šest decimalnih mesta) i 2/23409 (četiri decimale).

Može se izraziti kao verižni razlomak [1; 1, 2, 1, 2, 1, 2, 1, …] (niz A040001 u Enciklopedija nizova celih brojeva na mreži), proširen sa desne strane. Tako da je tačno reći:

{\begin{bmatrix}1&2\\1&3\end{bmatrix}}^{n}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}

onda kada $n\to \infty$ :

{\sqrt {3}}=2\cdot {\frac {a_{22}}{a_{12}}}-1

Može se izraziti preko generalizovanog verižnog razlomaka kao što su

[2;-4,-4,-4,...]=2-{\cfrac {1}{4-{\cfrac {1}{4-{\cfrac {1}{4-\ddots }}}}}}

što je [1; 1, 2, 1, 2, 1, 2, 1, …] ocenjeno na svakom drugom terminu.

Sledeći ugneždeni niz kvadratnih izraza konvergiraju ka √3 :

\!\ {\sqrt {3}}=2-2\left({\frac {1}{2}}-\left({\frac {1}{2}}-\left({\frac {1}{2}}-\left({\frac {1}{2}}-\dots \right)^{2}\right)^{2}\right)^{2}\right)^{2}={\frac {7}{4}}-4\left({\frac {1}{16}}+\left({\frac {1}{16}}+\left({\frac {1}{16}}+\left({\frac {1}{16}}+\dots \right)^{2}\right)^{2}\right)^{2}\right)^{2}.

Dokaz iracionalnosti

Ovaj dokaz iracionalnost za √3 koristi Pjer de Fermaovu metodu beskonačnog porekla :

Pretpostavimo da je √3 racionalan i izrazite ga na najniži mogući način (tj. kao potpuno smanjeni razlomak ) kao $m / n$ za prirodne brojeve $m$ i $n$ .

Stoga će množenje sa 1 dati jednak izraz:

{\frac {m({\sqrt {3}}-q)}{n({\sqrt {3}}-q)}}

gde je $q$ najveći celi broj manji od √3 . Imajte na umu da su i brojilac i imenilac pomnoženi sa brojem manjim od 1.

Pomoću ovoga i množenjem i brojioca i imenilaca dobijamo:

{\frac {m{\sqrt {3}}-mq}{n{\sqrt {3}}-nq}}

Slijedi da se $m$ može zamijeniti sa $\sqrt 3 n$ :

{\frac {n{\sqrt {3}}^{2}-mq}{n{\sqrt {3}}-nq}}

Zatim se √3 takođe može zameniti sa $m / n$ u nazivniku:

{\frac {n{\sqrt {3}}^{2}-mq}{n{\frac {m}{n}}-nq}}

Kvadrat √3 se može zameniti sa 3. Kako se $m / n$ množi sa $n$ , njihov proizvod jednak je $m$ :

{\frac {3n-mq}{m-nq}}

Tada se √3 može izraziti nižim izrazima od $m / n$ (pošto je prvi korak smanjio veličine od brojioca i imenioca, a sledeći koraci ih nisu promenili) kao $3 n - mq / m - nq$ , što je suprotnost hipotezi da je $m / n$ najniži. ^[3]

Alternativni dokaz za to je pretpostavka da je $\sqrt 3 = m / n$ sa $m / n$ potpuno smanjeni razlomak :

Množavanje sa $n$ obe strane, a zatim kvadriranjem daje

3n^{2}=m^{2}.

Pošto je leva strana deljiva sa 3, tako je i desna strana, zahtevajući da $m$ bude deljiv sa 3. Tada se $m$ može izraziti kao $3 k$ :

3n^{2}=(3k)^{2}=9k^{2}

Stoga, deljenje obe strane sa 3 daje:

n^{2}=3k^{2}

Kako je desna strana deljiva sa 3, tako je i leva strana, pa je i $n$ . Dakle, kako su i $n$ i $m$ deljivi sa 3, oni imaju zajednički delilac i $m / n$ nije potpuno smanjeni raѕlomak, suprotstavljena izvornoj premisi.

Geometrija i trigonometrija

Visina jendakostraničnog trougla sa ivicom dužine 2 je √3. (Ekvivalentno sa dužom katetom od 30-60-90 trougla sa hipotenuzom od 2.)

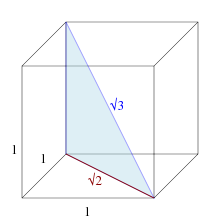
Kvadratni koren od 3 se može naći kao dužina hipotenuze jednakostraničnog trougla koji obuhvata krug prečnika 1.

Ako je jednakostranični trougao sa stranama dužine 1 podeljen na dva jednaka dela, deljenjem unutrašnjeg ugla kako bi napravili prav ugao sa jednom stranom, prav ugla trouglove hipotenuze je dužina jedan i strane su dužine 1/2 i √3/2. Iz ovoga je trigonometrijska funkcija tangente od 60° jednaka √3 i sinus od 60° i kosinus 30° i jednake √3/2.

Kvadratni koren od 3 se takođe pojavljuje u algebarskim izrazima za razne druge trigonometrijske konstante, uključujući ^[4] sinus od 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84°, i 87°.

To je rastojanje između paralelnih strana pravilnog šestougla sa stranicama dužine 1. Na kompleksnoj ravni, to rastojanje se izražava kao $i \sqrt 3$ pomenuto u nastavku.

To je dužina dijagonale jedinične kocke .

Vesica piscis ima odnos glavne ose do manje ose jednak 1: √3, što se može pokazati konstrukcijom dva jednakostranična trougla u sebi.

Kvadratni koren od −3

Množenjem √3 pomoću imaginarne jedinice daje kvadratni koren -3, koji je imaginarni broj . Tačnije,

{\sqrt {-3}}=\pm {\sqrt {3}}i

(vidi kvadratni koren negativnih brojeva). To je Ajzenštajnov ceo broj. Naime, izražava se kao razlika dva nerealna kubna korena od 1 (koji su Ajzenštajnovi celi brojevi).

Druge namene

Energetika

U elektroenergetici, napon između dve faze u trofaznom sistemu je jednaka √3 puta liniji neutralnog napona. To je zato što bilo koje dva faze su 120° razmaknute, i dve tačke na krugu od 120 stepeni su razdvojene √3 puta poluprečnika (vidi primere geometrije gore).

Vidi još

Reference

^ Łukasz Komsta. „Computations | Łukasz Komsta”. komsta.net. Arhivirano iz originala 04. 11. 2016. g. Pristupljeno 24. 9. 2016.
^ Knorr, Wilbur R. (1976), „Archimedes and the measurement of the circle: a new interpretation”, Archive for History of Exact Sciences, 15 (2): 115—140, JSTOR 41133444, MR 0497462, doi:10.1007/bf00348496 .
^ Grant, M.; Perella, M. (jul 1999). „Descending to the irrational”. Mathematical Gazette. 83 (497): 263—267. doi:10.2307/3619054.
^ Julian D. A. Wiseman Sin and Cos in Surds

Literatura

S., D.; Jones, M. F. (1968). „22900D approximations to the square roots of the primes less than 100”. Mathematics of Computation. 22 (101): 234—235. JSTOR 2004806. doi:10.2307/2004806.
Uhler, H. S. (1951). „Approximations exceeding 1300 decimals for √3, 1/√3, sin( $π$ /3) and distribution of digits in them”. Proc. Natl. Acad. Sci. U.S.A. 37 (7): 443—447. PMC 1063398 . PMID 16578382. doi:10.1073/pnas.37.7.443. templatestyles stripmarker u |title= na poziciji 142 (pomoć)
Wells, D. (1997). The Penguin Dictionary of Curious and Interesting Numbers (Revised izd.). London: Penguin Group. str. 23.

Spoljašnje veze

Teodorova konstanta na Math World
[1] Kevin Braun
[2] E.B. Davis

[1] Łukasz Komsta. „Computations | Łukasz Komsta”. komsta.net. Arhivirano iz originala 04. 11. 2016. g. Pristupljeno 24. 9. 2016.

[2] Knorr, Wilbur R. (1976), „Archimedes and the measurement of the circle: a new interpretation”, Archive for History of Exact Sciences, 15 (2): 115—140, JSTOR 41133444, MR 0497462, doi:10.1007/bf00348496 .

[Grant-3] Grant, M.; Perella, M. (jul 1999). „Descending to the irrational”. Mathematical Gazette. 83 (497): 263—267. doi:10.2307/3619054.

[4] Julian D. A. Wiseman Sin and Cos in Surds

[1]

[2]

[3]

[4]