Kratkoročna Furijeova transformacija

Kratkoročna Furijeova transformacija je Furijeova transformacija koja se koristi za određivanje sinusoidne frekvencije i faznog sadržaja lokalnih odseka signala kako se tokom vremena menja. ^[1] U praksi, postupak izračunavanja ove transformacije sastoji se od deljenja dužih vremenskih signala na kraće segmente jednake dužine, a zatim zasebno izračunati Furijeovu transformaciju na svakom kraćem segmentu. Ovo otkriva Furijeov spektar na svakom kraćem segmentu. Tada obično postavlja promenljivi spektar kao funkciju vremena.

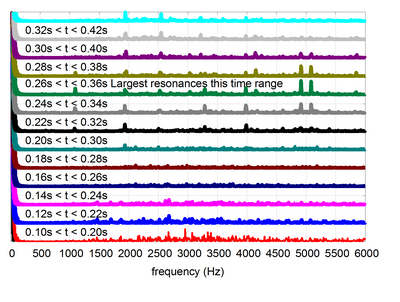
Napredna kratkoročna Furijeova transformacija

Vremenski kontinualna kratkoročna Furijeova transformacija

Jednostavno, u slučaju kontinuiranog vremena, funkcija koja se transformiše množi se prozorskom funkcijom koja je samo kratko vreme ne postoji. Fourierova transformacija (jednodimenzionalna funkcija) rezultirajućeg signala uzima se dok se prozor pomiče duž vremenske osi, rezultirajući dvodimenzionalnim prikazom signala. Matematički, ovo se piše kao:

\mathbf {STFT} \{x(t)\}(\tau ,\omega )\equiv X(\tau ,\omega )=\int _{-\infty }^{\infty }x(t)w(t-\tau )e^{-i\omega t}\,dt

gde $w(\tau )$ jeste funkcija prozora, obično Hanov prozor ili Gausov prozor koji je centriran oko nule a $x(t)$ jeste signal koji treba transformisati (imajte na umu razliku između funkcije prozora $w$ i frekvencije $\omega$ ). $X(\tau ,\omega )$ u suštini je Furijeova transformacija $x(t)w(t-\tau )$ , složena funkcija koja predstavlja fazu i jačinu signala tokom vremena i frekvencije. Često se odmotavanje faza upotrebljava duž jedne ili obe vremenske ose, $\tau$ i osne frekvencije, $\omega$ , da se suzbije bilo kakav prekid skoka faznog rezultata kratkoročne Furijeove transformacije. Vremenski indeks $\tau$ obično se smatra „ sporim “ vremenom i obično se ne izražava u tako visokoj rezoluciji kao vreme $t$ .

Kratkoročna Furijeova transformacija u diskretnom vremenu

U diskretnom vremenskom slučaju, podaci koji se transformišu mogu se raščlaniti na delove ili okvire (koji se obično preklapaju, da bi se smanjili artefakti na granici). Svaki komad se transformiše Furijeom transformacijom, a složen rezultat se dodaje u matricu koja beleži veličinu i fazu za svaku tačku u vremenu i frekvenciji. To se može izraziti kao:

\mathbf {STFT} \{x[n]\}(m,\omega )\equiv X(m,\omega )=\sum _{n=-\infty }^{\infty }x[n]w[n-m]e^{-j\omega n}

slično, sa signalom x[n] i prozorom w[n]. U ovom slučaju, m je diskretan i ω je kontinualan, ali u većini tipičnih primena STFT se izvodi na računaru pomoću brze Furijeove transformacije, tako da su obe promenljive diskretne i kvantizovane .

Veličina u kvadraturi kratkoročne Furijeove transformaciej daje spektrogramski prikaz spektralne gustoće snage funkcije:

\operatorname {spectrogram} \{x(t)\}(\tau ,\omega )\equiv |X(\tau ,\omega )|^{2}

Pogledajte i modifikovanu diskretnu transformaciju kosinusa, koja je takođe Furijeova transformacija koja koristi prozore koji se preklapaju.

Klizna diskretna Furijeova transformacija

Ako je poželjan samo mali broj ω ili ako se želi da se kratkoročna Furijeova transformacija procenjuje za svaki pomak m prozora, tada se ona može efikasnije proceniti koristeći klizni DFT algoritam. ^[2]

Inverzna kratkoročna Furijeova transformacija

Kratkoročna Furijeova transformacija je invertibilna, to jest, izvorni signal se može povratiti iz transformacije pomoću inverzne kratkoročne Furijeove transformacije. Najprihvaćeniji način pretvaranja kratkoročne Furijeove transformacije je korišćenjem metode preklapanja i dodavanja, koja takođe omogućava izmene u složenom spektru kratkoročne Furijeove transformacije. Ovo čini svestranim metode obrade signala ^[3] i naziva se preklapanjem i dodavanjem modifikacija.

Vremenski kontinuirana kratkoročna Furijeova transformacija

S obzirom na širinu i definiciju prozorske funkcije w(t), u početku zahtevamo da se površina funkcije prozora umanji tako da

\int _{-\infty }^{\infty }w(\tau )\,d\tau =1.

\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =1\quad \forall \ t

x(t)=x(t)\int _{-\infty }^{\infty }w(t-\tau )\,d\tau =\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau .

Kontinualna Furijeova transformacija je

X(\omega )=\int _{-\infty }^{\infty }x(t)e^{-j\omega t}\,dt.

Ako zamenimo h(t) odozgo:

X(\omega )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau \right]\,e^{-j\omega t}\,dt

=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,d\tau \,dt.

Menjanje redosleda integracije:

X(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\,d\tau

=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-j\omega t}\,dt\right]\,d\tau

=\int _{-\infty }^{\infty }X(\tau ,\omega )\,d\tau .

Dakle, Furijeova transformacija može se posmatrati kao vrsta faznog koherentnog suma svih STFT-ova k ( t ). Pošto je inverzna Fourierova transformacija

x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\omega )e^{+j\omega t}\,d\omega ,

tada se x(t) može povratiti iz X(τ, ω) kao

x(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\tau \,d\omega .

ili

x(t)=\int _{-\infty }^{\infty }\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega \right]\,d\tau .

Može se videti, da je u poređenju sa gorenavedenim „talasom“ prozora od h(t)

x(t)w(t-\tau )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+j\omega t}\,d\omega .

inverzna Furijeova transformacija X(τ, ω) za τ fiksna.

Pitanja rezolucije

Jedna od zamki kratkoročne Furijeove transformacije je ta što ima fiksnu rezoluciju. Širina funkcije prozora odnosi se na to kako je signal predstavljen - on određuje da li postoji dobra frekvenciona rezolucija (frekventne komponente blizu međusobno se mogu razdvojiti) ili dobra vremenska rezolucija (vreme u kome se frekvencije menjaju). Široki prozor daje bolju rezoluciju frekvencije, ali lošu vremensku rezoluciju. Uži prozor daje dobru vremensku rezoluciju, ali slabu frekvenciju. To se naziva uskopojasna i širokopojasna transformacija.

Ovo je jedan od razloga za stvaranje valne transformacije i multiresolucijske analize, koji mogu dati dobru vremensku rezoluciju za visokofrekventne događaje i dobru frekvencijsku rezoluciju za događaje sa niskim frekvencijama, kombinacija koja je najprikladnija za mnoge stvarne signale.

Ovo svojstvo je povezano sa Heisenbergovim principom neizvesnosti, ali nije direktno - videti ograničenje Gabora za raspravu. Proizvod standardnog odstupanja u vremenu i frekvenciji je ograničen. Granica principa nesigurnosti (najbolje istovremeno rešenje oba) se postiže Gaussovom funkcijom prozora, jer Gaussian minimizira princip Fourierove nesigurnosti . To se naziva Gaborova transformacija (i modifikacijama za multirezoluciju postaje Morlet- ova valutna transformacija).

Može se razmotriti STFT za promenu veličine prozora kao dvodimenzionalna domena (vreme i frekvencija), kao što je ilustrovano u donjem primeru, koji se može izračunati promenom veličine prozora. Međutim, ovo više nije strogo predstavljanje vremenske frekvencije - kernel nije konstantan tokom celog signala.

Primer

Koristite sledeće uzorke signala $x(t)$ koji su sastavljeni od skupa četiri talasa sinusoidnog oblika spojenih u nizu. Svaki talasni oblik sastoji se samo od jedne od četiri frekvencije (10, 25, 50, 100 Hz ). Definicija $x(t)$ je:

x(t)={\begin{cases}\cos(2\pi 10t)&0\,\mathrm {s} \leq t<5\,\mathrm {s} \\\cos(2\pi 25t)&5\,\mathrm {s} \leq t<10\,\mathrm {s} \\\cos(2\pi 50t)&10\,\mathrm {s} \leq t<15\,\mathrm {s} \\\cos(2\pi 100t)&15\,\mathrm {s} \leq t<20\,\mathrm {s} \\\end{cases}}

Zatim se uzorkuje na 400 Hz. Dobijeni su sledeći spektrogrami:

25 ms prozor	125 ms prozor
Prozor od 375 ms	1000 ms prozora

Prozor od 25 ms omogućava nam da identifikujemo tačno vreme u kome se signali menjaju, ali precizne frekvencije je teško prepoznati. Na drugom kraju skale, prozor od 1000 ms omogućava da se frekvencije tačno vide, ali vreme između promena frekvencije je zamagljeno.

Objašnjenje

To se takođe može objasniti referencom na frekvenciju uzorkovanja i Nikuist frekvenciju .

Pogledajte prozor N uzoraka iz proizvoljnog signala realne vrednosti brzinom uzorkovanja f _s . Preuzimanje Fourierove transformacije daje N složene koeficijente. Od ovih koeficijenata korisna je samo polovina (poslednji N / 2 je složen konjugat prve N / 2 obrnutim redosledom, jer je to stvarni signal).

Ovi N / 2 koeficijenti predstavljaju frekvencije od 0 do f _s / 2 (Nikuist), a dva uzastopna koeficijenta međusobno su rastavljena f _s / N Hz.

Da biste povećali frekvencijsku razlučivost prozora, razmak koeficijenata treba smanjiti. Postoje samo dve promenljive, ali smanjenje f _s (i održavanje N konstantnog) uzrokovaće da se poveća veličina prozora - jer sada ima manje uzoraka po jedinici vremena. Druga alternativa je povećanje N, ali to opet uzrokuje povećanje veličine prozora. Stoga svaki pokušaj povećanja rezolucije frekvencije uzrokuje veću veličinu prozora, a samim tim i smanjenje vremenske razlučivosti, i obrnuto.

Rejlova frekvencija

Kako je Nikuist-ova frekvencija ograničenje u maksimalnoj frekvenciji koja se može smisleno analizirati, tako je i Raileigh-ova frekvencija ograničenje na minimalnu frekvenciju.

Raileigh-ova frekvencija je minimalna frekvencija koja se može riješiti vremenskim vremenskim okvirom. ^[4] ^[5]

S obzirom na vremenski prozor u trajanju od Τ sekunde, najmanja frekvencija koja se može razrešiti je 1 / Τ Hz.

Raileigh-ova frekvencija važan je aspekt u primjeni kratkotrajne Fourier-ove transformacije (STFT), kao i bilo koje druge metode harmoničke analize na signalu konačne dužine zapisa. ^[6] ^[7]

Aplikacija

Kratkoročne Furijeove transformacije, kao i standardne Furijeove transformacije i drugi alati se često koriste za analizu muzike. Spektrogram, na primer, može da prikazuje frekvenciju na vodoravnoj osi, a najniže frekvencije levo, a najviše sa desne strane. Visina svake trake (povećana bojom) predstavlja amplitudu frekvencija unutar tog opsega. Dimenzija dubine predstavlja vreme, gde je svaka nova traka bila zasebna posebna transformacija. Audio inženjeri koriste ovu vrstu vizuelnog materijala za pribavljanje informacija o audio uzorku, na primer, za pronalaženje frekvencija specifičnih zvukova (naročito kada se koriste sa većom rezolucijom frekvencije) ili za pronalaženje frekvencija koje mogu biti manje ili više rezonantne u prostoru u kome signal jeste snimljen. Ove informacije se mogu koristiti za izjednačavanje ili podešavanje drugih audio efekata.

Implementacija

Originalna funkcija

X(t,f)=\int _{-\infty }^{\infty }w(t-\tau )x(\tau )e^{-j2\pi f\tau }d\tau

Pretvaranje u diskretni oblik:

t=n\Delta _{t},f=m\Delta _{f},\tau =p\Delta _{t}

X(n\Delta _{t},m\Delta _{f})=\sum _{-\infty }^{\infty }w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}\Delta _{t}

Pretpostavljajući prethodno

w(t)\cong 0{\text{ for }}|t|>B,{\frac {B}{\Delta _{t}}}=Q

Tada možemo upisati originalnu funkciju u

X(n\Delta _{t},m\Delta _{f})=\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}\Delta _{t}

Direktna primena

Ograničenja

a. Nikvistov kriterijum (izbegavanje efekta alijasinga):

\Delta _{t}<{\frac {1}{2\Omega }}

, gde

\Omega

jeste širina opsega od

x(\tau )w(t-\tau )

Metoda zasnovana na brzoj Furijeovoj transformaciji

Ograničenje

a. $\Delta _{t}\Delta _{f}={\tfrac {1}{N}}$ , gde $N$ je celi broj

b. $N\geq 2Q+1$

v. Nikvistov kriterijum (izbegavanje efekta alijasinga):

\Delta _{t}<{\frac {1}{2\Omega }}

,

\Omega

je širina opsega od

x(\tau )w(t-\tau )

X(n\Delta _{t},m\Delta _{f})=\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-{\frac {2\pi jpm}{N}}}\Delta _{t}

{\text{ако је }}q=p-(n-Q),{\text{ следи да је }}p=(n-Q)+q

X(n\Delta _{t},m\Delta _{f})=\Delta _{t}e^{\frac {2\pi j(Q-n)m}{N}}\sum _{q=0}^{N-1}x_{1}(q)e^{-{\frac {2\pi jqm}{N}}}

{\text{при чему је }}x_{1}(q)={\begin{cases}w((Q-q)\Delta _{t})x((n-Q+q)\Delta _{t})&0\leq q\leq 2Q\\0&2Q<q<N\end{cases}}

Rekurzivna metoda

Ograničenje

a. $\Delta _{t}\Delta _{f}={\tfrac {1}{N}}$ , gde $N$ je celi broj

b. $N\geq 2Q+1$

v. Nikvistov kriterijum (izbegavanje efekta alijasinga):

\Delta _{t}<{\frac {1}{2\Omega }}

,

\Omega

je širina opsega od

x(\tau )w(t-\tau )

g. Samo za implementaciju pravouglog oblika kratkoročne Furijeove transformacije

Pravougli prozor nameće ograničenje

w((n-p)\Delta _{t})=1

Zamena daje:

{\begin{aligned}X(n\Delta _{t},m\Delta _{f})&=\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})&x(p\Delta _{t})e^{-{\frac {j2\pi pm}{N}}}\Delta _{t}\\&=\sum _{p=n-Q}^{n+Q}&x(p\Delta _{t})e^{-{\frac {j2\pi pm}{N}}}\Delta _{t}\\\end{aligned}}

Smena promenljive $n -1$ za $n$ :

X((n-1)\Delta _{t},m\Delta _{f})=\sum _{p=n-1-Q}^{n-1+Q}x(p\Delta _{t})e^{-{\frac {j2\pi pm}{N}}}\Delta _{t}

Izračunavanje $X(\min {n}\Delta _{t},m\Delta _{f})$ za N-tačaka brze Furijeove transformacije:

X(n_{0}\Delta _{t},m\Delta _{f})=\Delta _{t}e^{\frac {j2\pi (Q-n_{0})m}{N}}\sum _{q=0}^{N-1}x_{1}(q)e^{-j{\frac {2\pi qm}{N}}},\qquad n_{0}=\min {(n)}

gde je

x_{1}(q)={\begin{cases}x((n-Q+q)\Delta _{t})&q\leq 2Q\\0&q>2Q\end{cases}}

Primena rekurzivne formule za izračunavanje $X(n\Delta _{t},m\Delta _{f})$

X(n\Delta _{t},m\Delta _{f})=X((n-1)\Delta _{t},m\Delta _{f})-x((n-Q-1)\Delta _{t})e^{-{\frac {j2\pi (n-Q-1)m}{N}}}\Delta _{t}+x((n+Q)\Delta _{t})e^{-{\frac {j2\pi (n+Q)m}{N}}}\Delta _{t}

Generalizacija diskretne Furijeove transformacije

Ograničenje

\exp {(-j2\pi pm\Delta _{t}\Delta _{f})}=\exp {(-j\pi p^{2}\Delta _{t}\Delta _{f})}\cdot \exp {(j\pi (p-m)^{2}\Delta _{t}\Delta _{f})}\cdot \exp {(-j\pi m^{2}\Delta _{t}\Delta _{f})}

pa je

X(n\Delta _{t},m\Delta _{f})=\Delta _{t}\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j2\pi pm\Delta _{t}\Delta _{f}}

X(n\Delta _{t},m\Delta _{f})=\Delta _{t}e^{-j2\pi m^{2}\Delta _{t}\Delta _{f}}\sum _{p=n-Q}^{n+Q}w((n-p)\Delta _{t})x(p\Delta _{t})e^{-j\pi p^{2}\Delta _{t}\Delta _{f}}e^{j\pi (p-m)^{2}\Delta _{t}\Delta _{f}}

Poređenje implementacija

Metod	Složenost
Direktna primena	$O(TFQ)$
Zasnovana na brzoj Furijeovoj transformaciji	$O(TN\log _{2}N)$
Rekurzija	$O(TF)$
Generalizacija diskretne Furijeove transformacije	$O(TN\log _{2}N)$

Vidi još

Procena spektralne gustine
Vremensko-frekventna reprezentacija
Metoda prenosa

Ostale vremenske frekvencije:

Funkcija distribucije u obliku konusa
Konstantno-K transformacija
Frakcionarna Furijeova transformacija
Gaborova transformacija
Njuvlandova transformacija
S transformacija
Talasna transformacija
Čirplet transformacija

Reference

^ Sejdić E.; Djurović I.; Jiang J. (2009). „Time-frequency feature representation using energy concentration: An overview of recent advances”. Digital Signal Processing. 19 (1): 153—183. doi:10.1016/j.dsp.2007.12.004.
^ E. Jacobsen and R. Lyons, The sliding DFT, Signal Processing Magazine vol. 20, issue 2, pp. 74–80 (March 2003).
^ Jont B. Allen (jun 1977). „Short Time Spectral Analysis, Synthesis, and Modification by Discrete Fourier Transform”. IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-25: 235—238.
^ „Arhivirana kopija” (PDF). Arhivirano iz originala (PDF) 04. 03. 2016. g. Pristupljeno 14. 12. 2019.
^ „What does "padding not sufficient for requested frequency resolution" mean? - FieldTrip toolbox”.
^ „Biased competition through variations in amplitude of gamma-oscillations”. J Comput Neurosci. 25 (1): 89—107. 2008. PMC 2441488 . PMID 18293071. doi:10.1007/s10827-007-0066-2.
^ Wingerden, Marijn van; Vinck, Martin; Lankelma, Jan; Pennartz, Cyriel M. A. (19. 5. 2010). „Theta-Band Phase Locking of Orbitofrontal Neurons during Reward Expectancy”. Journal of Neuroscience (na jeziku: engleski). 30 (20): 7078—7087. ISSN 0270-6474. PMID 20484650. doi:10.1523/JNEUROSCI.3860-09.2010.

Spoljašnje veze

DiskretniTFD - softver za računanje kratkotrajne Furijeove transformacije i druge vremenske frekvencije
Singularna spektralna analiza - MultiTaper Method Toolkit Arhivirano na sajtu Wayback Machine (16. januar 2014) - besplatni softver za analizu kratkih, bučnih vremenskih serija
kSpectra Toolkit za Mac OS Ks od SpectraVorks
Vremenski razvučena kratkoročna Furijeova transformacija za analizu vremenske frekvencije ultra širokopojasnih signala
Matlab klasa sa licencom BSD za izvođenje STFT i inverzne STFT
LTFAT - Besplatan (GPL) Matlab / Oktav paket alata za rad sa kratkotrajnim Furijeovim transformacijama i analizom vremenske frekvencije

[1] Sejdić E.; Djurović I.; Jiang J. (2009). „Time-frequency feature representation using energy concentration: An overview of recent advances”. Digital Signal Processing. 19 (1): 153—183. doi:10.1016/j.dsp.2007.12.004.

[2] E. Jacobsen and R. Lyons, The sliding DFT, Signal Processing Magazine vol. 20, issue 2, pp. 74–80 (March 2003).

[3] Jont B. Allen (jun 1977). „Short Time Spectral Analysis, Synthesis, and Modification by Discrete Fourier Transform”. IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-25: 235—238.

[4] „Arhivirana kopija” (PDF). Arhivirano iz originala (PDF) 04. 03. 2016. g. Pristupljeno 14. 12. 2019.

[5] „What does "padding not sufficient for requested frequency resolution" mean? - FieldTrip toolbox”.

[6] „Biased competition through variations in amplitude of gamma-oscillations”. J Comput Neurosci. 25 (1): 89—107. 2008. PMC 2441488 . PMID 18293071. doi:10.1007/s10827-007-0066-2.

[7] Wingerden, Marijn van; Vinck, Martin; Lankelma, Jan; Pennartz, Cyriel M. A. (19. 5. 2010). „Theta-Band Phase Locking of Orbitofrontal Neurons during Reward Expectancy”. Journal of Neuroscience (na jeziku: engleski). 30 (20): 7078—7087. ISSN 0270-6474. PMID 20484650. doi:10.1523/JNEUROSCI.3860-09.2010.

[1]

[2]

[3]

[4]

[5]

[6]

[7]