Logički napor

Metoda logičkog napora, termin koji su smislili Ivan Saterlend i Bob Sproul 1991. godine, je jednostavna tehnika koja se koristi za procenu kašnjenja u CMOS kolu. Ako se pravilno koristi, može pomoći u odabiru gejta za datu funkciju (uključujući broj neophodnih faza) i dimenzioniranju gejta kako bi se postiglo minimalno moguće kašnjenje za kolo.

Izvođenje kašnjenja u logičkom gejtu

Kašnjenje je izraženo kao osnovna jedinica kašnjenja, τ = 3RC, kašnjenje invertora koji pokreće identičan invertor bez ikakvog dodatnog kapaciteta koji se dodaje interkonekcijama ili drugim opterećenjima; broj bez jedinica povezan sa ovim je poznat kao normalizovano kašnjenje . (Neki autori preferiraju da definišu osnovnu jedinicu kašnjenja kao fenout od 4 kašnjenja – kašnjenje jednog invertora koji pokreće 4 identična intervtora). Apsolutno kašnjenje se tada jednostavno definiše kao proizvod normalizovanog kašnjenja gejta, d i τ :

d_{abs}=d\cdot \tau

U tipičnom procesu od 600nm τ je oko 50 ps. Za proces od 25nm, τ je oko 20ps. U modernom 45nm procesima kašnjenje je približno 4 do 5ps.

Normalizovano kašnjenje u logičkom gejtu može se izraziti kao zbir dva primarna termina: normalizovano parazitsko kašnjenje, p (koje je suštinsko kašnjenje gejta i može se naći uzimajući u obzir da gejt ne pokreće opterećenje) i napor stepena, f (što zavisi od opterećenja kao što je opisano u nastavku). Stoga,

d=f+p

Napor stepena je podeljen na dve komponente: logički napor, g, koji je odnos ulazne kapacitivnosti datog gejta prema onom invertoru koji može da isporuči istu izlaznu struju (i stoga je konstanta za određenu klasu gejta i može se opisati kao hvatanje intrinzičnih svojstava gejta), i električni napor, h, koji je odnos ulazne kapacitivnosti opterećenja i kapacitivnosti gejta. Imajte na umu da "logički napor" ne uzima u obzir opterećenje i stoga imamo izraz "električni napor" koji uzima u obzir opterećenje. Napor stepena je onda jednostavan:

f=gh

Kombinovanje ovih jednačina daje osnovnu jednačinu koja modelira normalizovano kašnjenje kroz jedan logički gejt:

d=gh+p

Procedura za izračunavanje logičkog napora jedne faze

CMOS invertori duž kritične putanje su obično dizajnirani sa gama jednakom 2. Drugim rečima, pFET invertora je projektovan sa dvostruko većom širinom (a samim tim i dvostrukom kapacitivnošću) od nFET invertora, kako bi se dobio približno isti pFET otpor kao i nFET otpor, kako bi se dobilo približno jednako povlačenje. gornja struja i silazna struja. ^[1] ^[2]

Izaberite veličine za sve tranzistore tako da je izlazni pogon gejta jednak izlaznom pogonu pretvarača napravljenog od PMOS veličine 2 i NMOS veličine 1.

Izlazni pogon gejta jednak je minimumu – preko svih mogućih kombinacija ulaza – izlaznog pogona gejta za taj ulaz.

Izlazni pogon gejta za dati ulaz je jednak pogonu na njegovom izlaznom čvoru.

Pogon na čvoru jednak je zbiru pogona svih tranzistora koji su uključeni i čiji je izvor ili odvod u kontaktu sa dotičnim čvorom. PMOS tranzistor je omogućen kada je napon na gejta 0. NMOS tranzistor je omogućen kada je napon na gejtu 1.

Kada su veličine izabrane, logički napor izlaza gejta je zbir širina svih tranzistora čiji je sours ili drejn u kontaktu sa izlaznim čvorom. Logički napor svakog ulaza do gejta je zbir širina svih tranzistora čiji je gejt u kontaktu sa tim ulaznim čvorom.

Logički napor celog gejta je odnos njenog izlaznog logičkog napora prema zbiru ulaznih logičkih napora.

Višestepene logičke mreže

Glavna prednost metode logičkog napora je da se brzo može proširiti na kola sastavljena od više faza. Ukupno normalizovano kašnjenje putanje D može se izraziti u smislu ukupnog napora putanje, F, i parazitnog kašnjenja putanje P (što je zbir pojedinačnih parazitskih kašnjenja):

D=NF^{1/N}+P

Napor putanje se izražava u smislu logičkog napora puta G (proizvod pojedinačnih logičkih napora gejtova) i električnog napora puta H (odnos opterećenja putanje i njene ulazne kapacitivnosti).

Za putanje gde svaki gejt pokreće samo jedan dodatni gejt (tj. sledeći gejt na putanji),

F=GH

Međutim, za kola koja se granaju, potrebno je uzeti u obzir dodatni napor grananja b; to je odnos ukupne kapacitivnosti koju pokreće gejt i kapacitivnosti na putu od interesa:

b={\frac {C_{onpath}+C_{offpath}}{C_{onpath}}}

Ovo daje napor grananja putanje B koji je proizvod napora grananja u pojedinačnim fazama; ukupan napor puta je tada

F=GHB

Može se videti da je b = 1 za gejtove koji pokreću samo jedan dodatan gejt, fiksirajući B = 1 i uzrokujući da se formula redukuje na raniju verziju bez grananja.

Minimalno kašnjenje

Može se pokazati da se u višestepenim logičkim mrežama minimalno moguće kašnjenje duž određene putanje može postići projektovanjem kola tako da napori stepena budu jednaki. Za datu kombinaciju gejtova i poznatog opterećenja, B, G i H su svi fiksni, što dovodi do toga da je F fiksiran; stoga pojedinačni gejtovi treba da budu tako dimenzionirani da su pojedinačni napori stepena

f=F^{1/N}

gde je N broj stepeni u kolu.

Primeri

Kašnjenje u invertoru

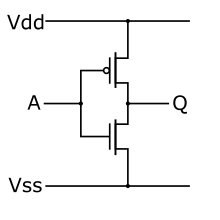
Po definiciji, logički napor g invertora je 1. Ako invertor pokreće ekvivalentni invertor, električni napor h je takođe 1.

Parazitno kašnjenje p invertora je takođe 1 (ovo se može naći razmatranjem Elmoreovog modela kašnjenja invertora).

Prema tome, ukupno normalizovano kašnjenje invertora koji pokreće ekvivalentni invertor je

d=gh+p=(1)(1)+1=2

Kašnjenje u NI i NILI gejtu

Logički napor NI gejta sa dva ulaza je izračunato kao g = 4/3 jer NI gejt sa ulaznom kapacitivnošću 4 može da pokreće istu struju kao i invertor, sa ulaznim kapacitetom 3. Slično, logički napor NI gejta sa dva ulaza može se naći kao g = 5/3. Zbog manjeg logičkog napora, NI gejtovi su tipično poželjnije nego NILI gejtovi.

Za veće gejtove, logičan napor je sledeći:

Logički napor za ulaze statičkih CMOS gejtove, sa gama = 2
Tip gejta	1	2	3	4	5	n
	Broj ulaza
Invertor	1	N/A	N/A	N/A	N/A	N/A
NI	N/A	${\frac {4}{3}}$	${\frac {5}{3}}$	${\frac {6}{3}}$	${\frac {7}{3}}$	${\frac {n+2}{3}}$
NILI	N/A	${\frac {5}{3}}$	${\frac {7}{3}}$	${\frac {9}{3}}$	${\frac {11}{3}}$	${\frac {2n+1}{3}}$

Normalizovano parazitsko kašnjenje NI i NILI gejtova je jednako broju ulaza.

Stoga je normalizovano kašnjenje NI gejta sa dva ulaza koja pokreće identičnu kopiju sebe (tako da je električni napor 1)

d=gh+p=(4/3)(1)+2=10/3

a za gejt NILI sa dva ulaza kašnjenje je

d=gh+p=(5/3)(1)+2=11/3

Reference

^ Bakos, Jason D. „Fundamentals of VLSI Chip Design”. University of South Carolina. str. 23. Arhivirano iz originala 8. 11. 2011. g. Pristupljeno 8. 3. 2011. CS1 održavanje: Format datuma (veza)
^ Dielen, M.; Theeuwen, J. F. M. (1987). An Optimal CMOS Structure for the Design of a Cell Library. str. 11.

Dodatna literatura

Sutherland, Ivan E.; Sproull, Robert F.; Harris, David F. (1999). Logical Effort: Designing Fast CMOS Circuits. Morgan Kaufmann. ISBN 1-55860-557-6.
Weste, Neil H. E.; Harris, David (2011). CMOS VLSI Design: A Circuits and Systems Perspective, 3rd Ed. Pearson/Addison-Wesley. ISBN 978-0-321-54774-3.

[1] Bakos, Jason D. „Fundamentals of VLSI Chip Design”. University of South Carolina. str. 23. Arhivirano iz originala 8. 11. 2011. g. Pristupljeno 8. 3. 2011. CS1 održavanje: Format datuma (veza)

[2] Dielen, M.; Theeuwen, J. F. M. (1987). An Optimal CMOS Structure for the Design of a Cell Library. str. 11.

[1]

[2]