Poliedar
Poliedar je geometrijsko telo omeđeno sa četiri ili više mnogouglova (koji se nazivaju strane ili pljosnati poliedri) i kome su ivice duži. Sama reč je nastala kao složenica reči poli (πολυς), što znači mnogo, i reči edron (εδρον), što znači baza, površ, sedište.[1]
Poliedarska površ
[uredi | uredi izvor]Skup površi mnogouglova takvih da je svaka stranica svakog mnogougla ujedno i stranica još samo jednog mnogougla, obrazuju zatvorenu površ koja se naziva poliedarska površ. Deo geometrijskog prostora koji ograničava (zatvorena) poliedarska površ je unutrašnjost poliedarske površi.
Unija poliedarske površi i njene unutrašnjosti je poliedar.
- Površi mnogouglova, od kojih se sastoji poliedarska površ, nazivaju se strane (ili pljosni) poliedra, a stranice tih mnogouglova nazivaju se ivice poliedarske površi i poliedra.
- Rogljevi koje obrazuju strane poliedra sa jednim zajedničkim temenom su rogljevi poliedra, a vrhovi tih rogljeva su temena poliedra.
- Svaka duž koja spaja dva temena poliedra, a ne pripada nijednoj strani poliedra predstavlja dijagonalu poliedra.
- Svaka ravan koju određuju tri temena poliedra i ne sadrži nijednu stranu poliedra predstavlja dijagonalnu ravan poliedra.
Podela poliedra
[uredi | uredi izvor]Poliedri mogu biti konveksni i nekonveksni-konkavni.
- Poliedar je konveksan ukoliko svaka duž koja spaja njegove dve proizvoljne tačke pripada tom poliedru, u suprotnom slučaju poliedar je nekonveksan odnosno konkavan.
Konveksni Poliedri
[uredi | uredi izvor]- Konveksan poliedar leži samo sa jedne strane ravni svake svoje strane.
- Konveksan poliedar se može predstaviti kao presek konačnog broja poluprostora određenih ravnima njegovih strana.
Regularni poliedri
[uredi | uredi izvor]Poliedar čije su sve strane regularni podudarni mnogouglovi i čiji su svi rogljevi podudarni naziva se regularan poliedar.
Konveksni regularni poliedri - Platonova tela
[uredi | uredi izvor]Konveksni regularni poliedri su poznati pod nazivom Platonova tela. Njihove strane su podudarni pravilni mnogouglovi, a rogljevi su međusobno podudarni i konveksni. To znači da su sve strane jednog poliedra pravilni mnogouglovi sa istim brojem n međusobno jednakih stranica i u temenu svakog roglja se sustiče isti broj k tih mnogouglova.
Dualni poliedri
[uredi | uredi izvor]U geometriji poliedri se posmatraju u parovima. Svakom poliedru odgovara dualni poliedar koji nastaje metamorfozom datog poliedra u kojoj:
- svakom temenu polaznog poliedra odgovara strana novog poliedra
- svakoj strani polaznog poliedra odgovara teme novog poliedra
- svakoj ivici polaznog poliedra odgovara ivica novog poliedra.
Osobine
[uredi | uredi izvor]- Strana prelazi u teme novog poliedra, a njeno teme u stranu koja sadrži to teme.
- Teme prelazi u stranu novog poliedra, a svaka strana čije je to teme u teme te strane.
- Ivica koja spaja dva temena prelazi u zajedničku ivicu dve odgovarajuće strane novog poliedra.
- Zajednička ivica dve susedne strane poliedra prelazi u ivicu koja spaja odgovarajuća temena novog poliedra.
- Svaka strana poliedra je poligon sa određenim brojem svojih temena. Metamorfozom poligon prelazi u teme, a njegova temena u strane novog poliedra čije je to teme, odnosno strani odovara rogalj.
- Svako teme poliedra je teme jednog njegovog roglja. Teme prelazi u stranu, a strane poliedra koje se sustiču u tom temenu (strane roglja) u temena koja pripadaju toj strani novog poliedra.
- Dualni poliedar dualnog poliedra je polazni poliedar.
Dualni poliedri – Platonova tela
[uredi | uredi izvor]Strane konveksnog regularnog poliedra tipa {n, k} su pravilni poligoni sa n temena. Strana se preslikava u teme novog poliedra a, a njena temena u strane novog poliedra koje se sustiču u tom temenu. Dobija se rogalj sa n strana.
Temena konveksnog regularnog poliedra tipa su {n, k} su temena podudarnih rogljeva sa k strana. Teme roglja prelazi u stranu, a njegove strane (odnosno strane poliedra koje se sustiču u tom temenu) u k temena te strane novog poliedra.
- Dualni poliedar konveksnog regularnog poliedra tipa {n, k} je konveksni regularni poliedar tipa {k, n}.
Numeričke karakteristike Platonovih tela
[uredi | uredi izvor]Karakteristika poliedra:
- n – broj temena (stranica) strane poliedra
- k – broj strana koje se sustiču u istom temenu
- T – broj temena poliedra
- S – broj strana poliedra
- I – broj ivica poliedra
Diedar čine dve susedne strane sa zajedničkom ivicom koja predstavlja ivicu diedra. Svi diedralni uglovi jednog Platonovog tela su međusobno jednaki. Diedralni ugao se očitava u ravni normalnoj na ivicu diedra.
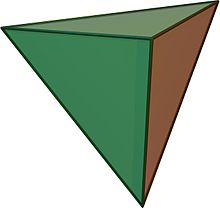
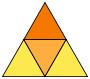
Platonova tela - tetraedar
[uredi | uredi izvor]- 4 temena
- 6 ivica
- 4 strane
- Diedralni ugao: 70.53°
Formule
[uredi | uredi izvor]| Površina | |
| Zapremina | |
| Poluprečnik opisane sfere | |
| Poluprečnik upisane sfere | |
| Visina | |
| Ugao između ivice i površi | |
| Ugao između dve površi |
Platonova tela – heksaedar
[uredi | uredi izvor]
- 8 temena
- 12 ivica
- 6 strana
- Diedralni ugao: 90°
Formule
[uredi | uredi izvor]
| Površina | |
| Zapremina | |
| Mala dijagonala[2] | |
| Velika dijagonala | |
| Poluprečnik upisane sfere | |
| Poluprečnik opisane sfere |
Platonova tela – oktaedar
[uredi | uredi izvor]
- 6 temena
- 12 ivica
- 8 strana
- Diedralni ugao: 109.47°
Formule
[uredi | uredi izvor]| Površina | |
| Zapremina | |
| Poluprečnik opisane sfere |
|
| Poluprečnik upisane sfere |
Platonova tela – dodekaedar
[uredi | uredi izvor]
- 20 temena
- 30 ivica
- 12 strana
- Diedralni ugao: 116.56°
Formule
[uredi | uredi izvor]| Površina | |
| Zapremina | |
| Poluprečnik upisane sfere |
|
| Poluprečnik opisane sfere |
Platonova tela – ikosaedar
[uredi | uredi izvor]
- 12 temena
- 30 ivica
- 20 strana
- Diedralni ugao: 138.19°
Formule
[uredi | uredi izvor]| Površina | |
| Zapremina | |
| Poluprečnik upisane sfere |
|
| Poluprečnik opisane sfere |
Izometrija poliedra
[uredi | uredi izvor]Uzajamno jednoznačno preslikavanje f: T1 → T2 poliedara (tela) T1, T2 u kome dolazi do očuvanja metrike odnosno očuvanja rastojanja između tačaka je izometrično preslikavanje ili izometrija. Geometrijske transformacije: translacija, rotacija, refleksija i njihova kompozicija (uzastopno izvođenje) u proizvoljnom poretku i proizvoljnom broju su izometrične transformacije.
Simetrije poliedra
[uredi | uredi izvor]Izometrično preslikavanje f : T → T poliedara T u samog sebe je simetrija. Grupa simetrija svakog poliedra sadrži sve moguće rotacije i sve moguće refleksije koje poliedar preslikavaju u samog sebe. Kompozicija simetrija jednog poliedra (u proizvoljnom poretku) je takođe jedna simetrija iz grupe svih mogućih simetrija tog poliedra.
Reference
[uredi | uredi izvor]Literatura
[uredi | uredi izvor]- Ljiljana Petruševski - Poliedri
- Cromwell, P.;Polyhedra, CUP hbk (1997), pbk. (1999).
- Grünbaum, B. (1994). „Polyhedra with Hollow Faces”. Ur.: Tibor Bisztriczky; Peter McMullen; Rolf Schneider; et al. Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational. Springer. str. 43—70. ISBN 978-94-010-4398-4.
- Grünbaum, B.; Are your polyhedra the same as my polyhedra? Discrete and comput. geom: the Goodman-Pollack festschrift, ed. Aronov et al. Springer (2003) pp. 461–488. (pdf Arhivirano na sajtu Wayback Machine (3. avgust 2016))
- Bertrand, J. (1858). Note sur la théorie des polyèdres réguliers, Comptes rendus des séances de l'Académie des Sciences, 46, pp. 79–82.
- Haeckel, E. (1904). Kunstformen der Natur. Available as Haeckel, E. Art forms in nature, Prestel USA (1998), ISBN 3-7913-1990-6, or online at https://web.archive.org/web/20090627082453/http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.html
- Smith, J. V. (1982). Geometrical And Structural Crystallography. John Wiley and Sons.
- Sommerville, D. M. Y. (1930). An Introduction to the Geometry of n Dimensions. E. P. Dutton, New York. (Dover Publications edition, 1958). Chapter X: The Regular Polytopes.
- Coxeter, H.S.M.; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8
- Whitney, Hassler (1932). „Congruent graphs and the connectivity of graphs”. Amer. J. Math. 54 (1): 150—168. JSTOR 2371086. doi:10.2307/2371086. hdl:10338.dmlcz/101067.
- Blind, Roswitha; Mani-Levitska, Peter (1987), „Puzzles and polytope isomorphisms”, Aequationes Mathematicae, 34 (2–3): 287—297, MR 921106, doi:10.1007/BF01830678
- Kalai, Gil (1988), „A simple way to tell a simple polytope from its graph”, Journal of Combinatorial Theory, Ser. A, 49 (2): 381—383, MR 964396, doi:10.1016/0097-3165(88)90064-7
- Kaibel, Volker; Schwartz, Alexander (2003). „On the Complexity of Polytope Isomorphism Problems”. Graphs and Combinatorics. 19 (2): 215—230. arXiv:math/0106093
 . doi:10.1007/s00373-002-0503-y. Arhivirano iz originala 2015-07-21. g.
. doi:10.1007/s00373-002-0503-y. Arhivirano iz originala 2015-07-21. g. - Büeler, B.; Enge, A.; Fukuda, K. (2000). „Exact Volume Computation for Polytopes: A Practical Study”. Polytopes — Combinatorics and Computation. str. 131. ISBN 978-3-7643-6351-2. doi:10.1007/978-3-0348-8438-9_6.
- Yao, Andrew Chi Chih (1981), „A lower bound to finding convex hulls”, Journal of the ACM, 28 (4): 780—787, MR 677089, doi:10.1145/322276.322289; Ben-Or, Michael (1983), „Lower Bounds for Algebraic Computation Trees”, Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing (STOC '83), str. 80—86, doi:10.1145/800061.808735
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd izd.), Oxford: Clarendon Press, MR 0124167.
- Gailiunas, P.; Sharp, J. (2005), „Duality of polyhedra”, International Journal of Mathematical Education in Science and Technology, 36 (6): 617—642, doi:10.1080/00207390500064049.
- Grünbaum, Branko (2003), „Are your polyhedra the same as my polyhedra?”, Ur.: Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, 25, Berlin: Springer, str. 461—488, CiteSeerX 10.1.1.102.755
 , ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21.
, ISBN 978-3-642-62442-1, MR 2038487, doi:10.1007/978-3-642-55566-4_21. - Grünbaum, Branko (2007), „Graphs of polyhedra; polyhedra as graphs”, Discrete Mathematics, 307 (3–5): 445—463, MR 2287486, doi:10.1016/j.disc.2005.09.037.
- Grünbaum, Branko; Shephard, G. C. (2013), „Duality of polyhedra”, Ur.: Senechal, Marjorie, Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, str. 211—216, ISBN 978-0-387-92713-8, MR 3077226, doi:10.1007/978-0-387-92714-5_15.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208.
- Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688
Spoljašnje veze
[uredi | uredi izvor]Opšta teorija
[uredi | uredi izvor]- Weisstein, Eric W. „Polyhedron”. MathWorld.
- Polyhedra Pages
- Uniform Solution for Uniform Polyhedra by Dr. Zvi Har'El
- Symmetry, Crystals and Polyhedra
Spisak i baza podataka poliedara
[uredi | uredi izvor]- Virtual Reality Polyhedra - The Encyclopedia of Polyhedra
- Electronic Geometry Models - Contains a peer reviewed selection of polyhedra with unusual properties.
- Polyhedron Models - Virtual polyhedra
- Paper Models of Uniform (and other) Polyhedra
Slobodni softver
[uredi | uredi izvor]- A Plethora of Polyhedra – An interactive and free collection of polyhedra in Java. Features includes nets, planar sections, duals, truncations and stellations of more than 300 polyhedra.
- Hyperspace Star Polytope Slicer - Explorer java applet, includes a variety of 3d viewer options.
- openSCAD - Free cross-platform software for programmers. Polyhedra are just one of the things you can model. The openSCAD User Manual is also available.
- OpenVolumeMesh - An open source cross-platform C++ library for handling polyhedral meshes. Developed by the Aachen Computer Graphics Group, RWTH Aachen University.
- Polyhedronisme Arhivirano na sajtu Wayback Machine (25. april 2012) - Web-based tool for generating polyhedra models using Conway Polyhedron Notation. Models can be exported as 2D PNG images, or as 3D OBJ or VRML2 files. The 3D files can be opened in CAD software, or uploaded for 3D printing at services such as Shapeways.
Resursi za pravljenje fizičkih modela
[uredi | uredi izvor]- Paper Models of Polyhedra Free nets of polyhedra
- Simple instructions for building over 30 paper polyhedra
- Polyhedra plaited with paper strips - Polyhedra models constructed without use of glue.

























