Pravilo sudnjeg dana

Pravilo sudnjeg dana ili algoritam sudnjeg dana je način na koji može da se izračuna dan nedelje prema zadatom datumu. On radi sa perpetualnim kalendarom jer se Gregorijanski kalendar ponavlja na svakih 400 godina.

Ovaj algoritam koji se služi mentalnim računanjem osmislio je Džon Konvej^[1]^[2] dobivši inspiraciju nakon što je pročitao rad Luisa Kerola^[3]^[4] o večitom kalendaru. Algoritam koristi činjenicu da svake godine postoji dan u nedelji (tzv. sudnji dan) na koji „padaju“ određeni datumi što se lako pamte, na primer 4.4. 6.6. 8.8. 10.10. 12.12. i poslednji dan februara uvek padaju na isti dan u bilo kojoj godini. Primena ovog algoritma sastoji se iz tri koraka:

Odrediti „usidren dan“ veka
Koristi taj dan da se izračuna sudnja godina
Izaberi najbliži datum od onih koji se lako pamte (4.4. 6.6. 8.8. 10.10. 12.12.), i izbroj dane po modulu 7 između tog datuma i datuma za koji se pitamo na koji dan nedelje pada.

Ova tehnika može se primeniti i na Gregorijanski kalendar nove ere ili Julijanski kalendar, iako će njihovi sudnji dani ponekad biti različiti dani godine.

Pošto ovaj algoritam gleda na dane kao brojeve po modulu 7, Džon Konvej je predložio se dani nedelje zovu (na engleskom) "Noneday" ili "Sansday" (za nedelju), "Oneday", "Twosday", "Treblesday", "Foursday", "Fiveday", i "Six-a-day". Postoji nekoliko jezika kao npr. portugalski ili galicijski koji zasnivaju neke nazive za dane na njihovoj poziciji u sedmici.

Algoritam je jednostavan i ne podrazumeva veliko predznanje aritmetike da bi mogao da se koristi za mentalno računanje. Konvej je mogao da odredi dan u sedmici za zadati datum za manje od dve sekunde. Da bi poboljšao svoju brzinu, vežbao je određivanje dana u sedmici na svom računaru, koji je bio isprogramiran da ga pita za nasumične datume svaki put kada se uključi.^[5]

Sudnji dan za neke godine

Sudnji dan za trenutnu godinu u gregorijanskom kalendaru je ponedeljak za 2016. godinu.

Za neke druge godine je:

**Sudnji dani za Gregorijanski kalendar**
Pon.	Uto.	Sre.	Čet.	Pet.	Sub.	Ned.	Pon.	Uto.	Sre.	Čet.	Pet.	Sub.	Ned.
1898	1899	1900	1901	1902	1903	→	1904	1905	1906	1907	→	1908	1909
1910	1911	→	1912	1913	1914	1915	→	1916	1917	1918	1919	→	1920
1921	1922	1923	→	1924	1925	1926	1927	→	1928	1929	1930	1931	→
1932	1933	1934	1935	→	1936	1937	1938	1939	→	1940	1941	1942	1943
→	1944	1945	1946	1947	→	1948	1949	1950	1951	→	1952	1953	1954
1955	→	1956	1957	1958	1959	→	1960	1961	1962	1963	→	1964	1965
1966	1967	→	1968	1969	1970	1971	→	1972	1973	1974	1975	→	1976
1977	1978	1979	→	1980	1981	1982	1983	→	1984	1985	1986	1987	→
1988	1989	1990	1991	→	1992	1993	1994	1995	→	1996	1997	1998	1999
→	2000	2001	2002	2003	→	2004	2005	2006	2007	→	2008	2009	2010
2011	→	2012	2013	2014	2015	→	2016	2017	2018	2019	→	2020	2021
2022	2023	→	2024	2025	2026	2027	→	2028	2029	2030	2031	→	2032
2033	2034	2035	→	2036	2037	2038	2039	→	2040	2041	2042	2043	→
2044	2045	2046	2047	→	2048	2049	2050	2051	→	2052	2053	2054	2055
→	2056	2057	2058	2059	→	2060	2061	2062	2063	→	2064	2065	2066
2067	→	2068	2069	2070	2071	→	2072	2073	2074	2075	→	2076	2077
2078	2079	→	2080	2081	2082	2083	→	2084	2085	2086	2087	→	2088
2089	2090	2091	→	2092	2093	2094	2095	→	2096	2097	2098	2099	2100

Napomena: Polja se pune horizontalno, preskačući svako kolonu za svaku prestupnu godinu. Ova tabela ima ciklus od 28 godina, sem u Gregorijanskom kalendaru kada su godine deljive sa 100 koje nisu deljive sa 400. Ceo ciklus traje 28 godina (1, 461 nedelja) u Julijanskom kalendaru, a 400 godina (20, 871 nedelja) u Gregorijanskom.

Bitni datumi koji uvek padaju na sudnji dan

Moguće je naći dan nedelje zadate kalendarske godine pomoću bliskog sudnjeg dana kao referentne tačke. Da bi se to olakšalo, sledi lista datuma koji se lako pamte za svaki mesec koji uvek padaju na sudnji dan.

Kao što je spomenuto iznad, poslednji dan februara određuje sudnji dan. Za januar, 3. januar je sudnji dan tokom neprestupnih godina, tok je 4. januar za prestupne godine, koji se mogu zapamtiti kao treći tokom tri od 4 godine, i kao četvrti u četvrtoj godini. Za mart, može se zapamtiti pseudo datum 0. mart, koji se odnosi na dan pre 1. marta to jest poslednji dan februara.

Za mesece od aprila do decembra, sudnji dani su oni sa istim rednim brojem dana i rednim brojem meseca uz to da je mesec paran (4.4. 6.6. 8.8. 10.10. 12.12.) gde svi mogu da se računaju kao sudnji dan. Neparan broj meseci može da se zapamti kao mnemonik „Ja radim od 9 do 5 u 7-11 radnji“ jer su 9/5, 7/11 sudnji dani, kao i 5/9 i 11/7 koji su takođe sudnji dani.

Mesec	Lak datum	Mesec/Dan	Mnemonik
Januar	3. januar (neprestupne godine), 4. januar (prestupna godina)	1/3 ili 1/4	treća godina u četiri i četvrti u četvrtoj
Februar	28. februar (neprestupne godine), 29. februar (prestupna godina)	2/28 ili 2/29	poslednji dan februara
Mart	"0 Mart"	3/0	poslednji dan februara
April	4. april	4/4	4/4, 6/6, 8/8, 10/10, 12/12
Maj	9. maj	5/9	9-do-5 u 7-11
Jun	6. jun	6/6	4/4, 6/6, 8/8, 10/10, 12/12
Jul	11. jul	7/11	9-do-5 u 7-11
Avgust	8. avgust	8/8	4/4, 6/6, 8/8, 10/10, 12/12
Septembar	5. septembar	9/5	9-do-5 u 7-11
Oktobar	10. oktobar	10/10	4/4, 6/6, 8/8, 10/10, 12/12
Novembar	7. novembar	11/7	9-do-5 u 7-11
Decembar	12. decembar	12/12	4/4, 6/6, 8/8, 10/10, 12/12

Pošto je sudnji dan za određenu godinu direktno povezan sa činjenicom da li se pitamo za prestupnu ili neprestupnu godinu, mora se uspostaviti razlika za januar i februar te godine.

Primeri

Da bi se našao dan nedelje katoličkog božića 2006. godine (2008 sudnji dan je bio utorak). Pošto je 12. decembar sudnji dan, 25. decembar će pošto je trinaesti dan posle 12. biti ponedeljak.

Treba i napomenuti da božić uvek pada na dan pre sudnjeg dana te godine. Uz to 4. jul (američki praznik dana državnosti) je uvek sudnji dan, kao i noć veštica (31. oktobar).

Da bi se našao dan nedelje za teroristički napad na „Bliznakinje“ koji se desio 11. septembra 2001. godine moramo prvo da znamo da je datum „sidro“ veka utorak, i da je sudnji dan za 2001. bio jedan dan unapred, to jest sreda. 5. septembar je tu najbliži sudnji dan, a 11. septembar je 6 dana kasnije i pada na utorak.

Nalaženje sudnjeg dana godine

Prvo uzimamo datum „sidro“ veka. Sledeća tabela pokazuje te datume za vekove od 1800 – 1899, 1900 – 1999, 200 – 2099, 2100 – 2199.

Vek	Sidro	Mnemonik	Indeks (dan nedelje)
1800–1899	Friday	—	5 (Fiveday)
1900–1999	Wednesday	We-in-dis-day (most living people were born in that century)	3 (Treblesday)
2000–2099	Tuesday	Y-Tue-K or Twos-day (Y2K was at the head of this century)	2 (Twosday)
2100–2199	Sunday	Twenty-one-day is Sunday (2100 is the start of the next century)	0 (Noneday)

Dalje, tražimo sudnji dan godine. Da bismo ovo postigli prema Konveju:

Podelimo poslednje dve cifre godine (taj broj ćemo zvati y) sa 12, i neka a bude floor tog količnika
Neka b bude ostatak te jednačine
Podelimo taj ostatak sa 4 i neka c bude floor količnika.
Neka d bude suma tri broja (d = a + b + c). (Ovde je moguće opet podeliti suma sa 7 i onda uzeti ostatak. Ovaj broj je ekvivalentan sumi poslednje dve cifre uzete godine plus floor te dve cifre podeljen sa 4).
Izbrojmo unapred napomenute brojeve dana (d ili ostatak od deljenja d sa 7) iz sidra da bi se dobio sudnji dan te godine.

Za 20. vek godina je 1966. na primer:

Kao što je opisano u tački 4 iznad, to je ekvivalentno sa:

Tako da sudnji dan za 1966. pada na ponedeljak.

Slično, sudnji dan za npr. 1966. je takođe ponedeljak:

Zašto ovo radi

Računanje sudnjeg dana je tačno izračunavanje broja dana između bilo kog datuma u baznoj godini sa i istog datuma u trenutnoj godini, a onda ostatak modulirati sa 7. Kada oba datuma dolaze posle prestupne godine, razlika je samo 365u + u/4 (zaokruženo). Ali 365 je jednako 52 * 7 + 1, tako da kada sklonimo ostatak ostaje nam

To nam daje jednostavnu formulu ako je korisnik sposoban da deli velike broje u sa 4 i 7. Na primer možemo da izračunamo:

Što daje isto rešenje kao u primeru iznad.

Broj 12 ulazi u algoritam kada se uzorak (u + u/4)mod 7 skoro ponavlja svakih 12 godina. Posle 12 godina, dobijamo (12 + 12/4) mod 7 = 15 mod 7 = 1. Ako zamenimo u sa u mod12, onda odbacujemo taj dodatni dan.

Metoda „nepar + 11“

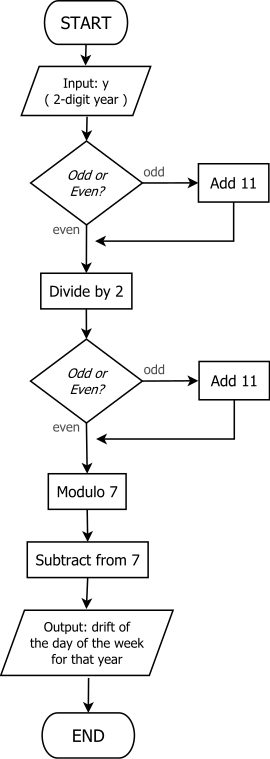
Jednostavnija metoda za nalaženje sudnjeg dana godine je otkrivena 2010. godine i opisana je u istraživanju Fonga i Voltersa koje je objavljeno. Ova metoda je ekvivalentna

\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}

.

Vrlo je prilagođena računanju u glavi, zato što joj nije potrebno deljenje sa 4 ili 12, a procedura se lako pamti jer se ponavlja ključno pravilo.

Ako proširimo ovo na nalaženje sudnjeg dana, procedura se često opisuje kao akumulacija ukupno 6 koraka, koji slede:

Neka T budu poslednje dve cifre godine
Ako je T neparno, dodaj 11
Sad podeli T sa dva
Ako je t neparno, dodaj 11
Sada neka T bude T = 7 − (T mod 7).
Broj T dana unapred od sidra veka da bi se dobio sudnji dan godine

Ako primenimo ovu metodu na 2005. na primer, koraci izgledaju ovako:

$T = 5$
$T = 5 + 11 = 16$ (dodajemo 11 jer je T neparno)
$T = 16 / 2 = 8$
$T = 8$ (ne radimo ništa jer je T parno)
$T = 7 - (8 mod 7) = 7 - 1 = 6$
Sudnji dan za 2005 = 6 + utorak = ponedeljak

Eksplicitna formula ove metode je:

-\left\lfloor {\frac {y+11(y\,{\bmod {2}})}{2}}+11\left({\frac {y+11(y\,{\bmod {2}})}{2}}{\bmod {2}}\right)\right\rfloor {\bmod {7}}

.

Iako vo možda može da izgleda zastrašujuće i komplikovano, u tsvari je vrlo jednostavno jer je zajednički podizraz $y + 11(y mod 2) / 2$ koji mora samo jednom da se izračuna.

Metoda slova

Godinin sudnji dan (DD) takođe može da se izračuna i sa radom sa slovima godine (DL).

DD = (3 - DL) mod 7

Napomena: A = 1, B = 2, ..., G = 0.

Za godinu 1966. slovo je B, tako da je sudnji dan DD = 3-2 =1 = ponedeljak.

Sudnji dan	Slovo
Nedelja	C, DC
Ponedeljak	B, CB
Utorak	A, BA
Sreda	G, AG
Četvrtak	F, GF
Petak	E, FE
Subota	D, ED

Pronalazak „sidra“ veka

Za Gregorijanski kalendar:

5 \times (c mod 4) mod 7 +

utorak = sidro.

Za Julijanski kalendar:

6 \times (c mod 7) mod 7 +

nedelja = sidro.

Napomena: $c = ⌊.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}year/100⌋$ .

Pregled svih sudnjih dana

Mesec	Datum	Broj sedmice *
Januar (neprestupne godine)	3, 10, 17, 24, 31	1–5
Januar (prestupne godine)	4, 11, 18, 25	1–4
Februar (common years)	7, 14, 21, 28	6–9
Februar (leap years)	1, 8, 15, 22, 29	5–9
Mart	7, 14, 21, 28	10–13
April	4, 11, 18, 25	14–17
Maj	2, 9, 16, 23, 30	18–22
Jun	6, 13, 20, 27	23–26
Jul	4, 11, 18, 25	27–30
Avgust	1, 8, 15, 22, 29	31–35
Septembar	5, 12, 19, 26	36–39
Oktobar	3, 10, 17, 24, 31	40–44
Novembar	7, 14, 21, 28	45–48
Decembar	5, 12, 19, 26	49–52

Tako je u neprestupnoj godini dan nedelje je jedan manji od nedelje.

Kompjuterska formula za pronalaženje sudnjeg dana godine

Za upotrebu i rad sa računarima, sledeće formula za pronalazak sudnjeg dana je vrlo prikladna:

Za Gregorijanski kalendar:

{\mbox{Doomsday}}={\mbox{Tuesday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor +\left\lfloor {\frac {y}{400}}\right\rfloor ={\mbox{Tuesday}}+5\times (y{\bmod {4}})+4\times (y{\bmod {1}}00)+6\times (y{\bmod {4}}00)

Na primer, godina 2009. ima sudnji dan nedelju prema Gregorijanskom kalendaru.

{\mbox{Saturday (6)}}{\bmod {7}}={\mbox{Tuesday (2)}}+2009+\left\lfloor {\frac {2009}{4}}\right\rfloor -\left\lfloor {\frac {2009}{100}}\right\rfloor +\left\lfloor {\frac {2009}{400}}\right\rfloor

Kao drugi primer, godina 1946 ima sudnji dan četvrtak:

{\mbox{Thursday (4)}}{\bmod {7}}={\mbox{Tuesday (2)}}+1946+\left\lfloor {\frac {1946}{4}}\right\rfloor -\left\lfloor {\frac {1946}{100}}\right\rfloor +\left\lfloor {\frac {1946}{400}}\right\rfloor

Za Julijanski kalednar:

{\mbox{Doomsday}}={\mbox{Sunday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor ={\mbox{Sunday}}+5\times (y{\bmod {4}})+3\times (y{\bmod {7}})

Ova formula može i da se primeni na proleptični Gregorijanski kalendar i na proleptični Julijanski kalendar. Oni koriste floor funkciju i astronomsko brojanje godina za godine pre nove ere.

Za poređenje, pogledati računanje u Julijanskom kalendaru.

Ciklus sudnjih dana od 400 godina

Od kad se uveo Gregorijanski kalendar, prošlo je 146 097 dana, ili tačno 20 871 sedmica, u 400 godina, sidro se ponavlja svaka 4 veka. Na primer sidro za 1700 – 1799 je sito kao i sidro za 2100 – 2199, to jest nedelja.

Potpuni 400- godišnji ciklus je prikazan u tabeli ispod. Vekovi su za Gregorijanski i proleptični Gregorijanski kalendar, sem ako nisu obeleženi sa J što označava Julijanski. Gregorijanske prestupne godine su označene.

Julijanski vekovi ——— Gregorijanski vekovi \ Godine	-1600J -900J -200J 500J 1200J 1900J 2600J 3300J — -1600 -1200 -800 -400 0 400 800 1200 1600 2000 2400 2800 3200 3600	-1500J -800J -100J 600J 1300J 2000J 2700J 3400J —	-1400J -700J 0J 700J 1400J 2100J 2800J 3500J — -1500 -1100 -700 -300 100 500 900 1300 1700 2100 2500 2900 3300 3700	-1300J -600J 100J 800J 1500J 2200J 2900J 3600J —	-1200J -500J 200J 900J 1600J 2300J 3000J 3700J — -1400 -1000 -600 -200 200 600 1000 1400 1800 2200 2600 3000 3400 3800	-1100J -400J 300J 1000J 1700J 2400J 3100J 3800J —	-1000J -300J 400J 1100J 1800J 2500J 3200J 3900J — -1300 -900 -500 -100 300 700 1100 1500 1900 2300 2700 3100 3500 3900
00 28 56 84	Uto.	Pon.	Ned.	Sub.	Pet.	Čet.	Sre.
01 29 57 85	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.	Čet.
02 30 58 86	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.
03 31 59 87	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.
04 32 60 88	Ned.	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.
05 33 61 89	Pon.	Ned.	Sub.	Pet.	Čet.	Sre.	Uto.
06 34 62 90	Uto.	Pon.	Ned.	Sub.	Pet.	Čet.	Sre.
07 35 63 91	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.	Čet.
08 36 64 92	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.
09 37 65 93	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.
10 38 66 94	Ned.	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.
11 39 67 95	Pon.	Sub.	Sub.	Pet.	Čet.	Sre.	Uto.
12 40 68 96	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.	Čet.
13 41 69 97	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.
14 42 70 98	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.
15 43 71 99	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.
16 44 72	Pon.	Ned.	Sub.	Pet.	Čet.	Sre.	Uto.
17 45 73	Uto.	Pon.	Ned.	Sub.	Pet.	Čet.	Sre.
18 46 74	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.	Čet.
19 47 75	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.
20 48 76	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.
21 49 77	Ned.	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.
22 50 78	Pon.	Ned.	Sub.	Pet.	Čet.	Sre.	Uto.
23 51 79	Uto.	Pon.	Ned.	Sub.	Pet.	čet.	Sre.
24 52 80	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.	Pet.
25 53 81	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.	Sub.
26 54 82	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.	Ned.
27 55 83	Ned.	Sub.	Pet.	Čet.	Sre.	Uto.	Pon.

Negativne godine koriste astronomsko brojanje. Godina 25. p. n. e. je -24, kao što je prikazano u koloni.

**Ponavljanje gregorijanskih sudnjih dana u ciklusu od 400 godina po danima i tipu godine:**
Nedelja	Ponedeljak	Utorak	Sreda	Četvrtak	Petak	Subota	Ukupno
Neprestupne godine	43	43	43	43	44	43	44	303
Prestupne godine	13	15	13	15	13	14	14	97
Ukupno	56	58	56	58	57	57	58	400

Prestupna godina sa ponedeljkom kao sudnjim danom znači da je nedelja jedna od 97 preskočenih dana u sekvenci od 497-dmo dnevne sekvence. Tako je ukupan broj godina sa nedeljom kao sudnjim danom jednak 71 minus broj prestupnih godina sa ponedeljkom kao sudnjim danom itd. Pošto je ponedeljak kao sudnji dan preskočen 29. februara 2000. godine i patern prestupnih dana je simetričan sa tim danom, ponavljanje sudnjih dana po danima nedelje (dodajemo prestupne i neprestupne godine) su simetrične sa ponedeljkom. Ponavljanje sudnjih dana u prestupnim godinama su simetrični sa sudnjim danom 2000. godine to jest utorkom.

Ponavljanje konkretnog dana kao nekog dana sedmice može lako se dobije iz formule iznad.

Na primer, 28. februar je jedan dan posle sudnjeg dana prethodne godine, tako da je 58 puta utorak, četvrtak i nedelja itd. 29. februar je sudnji dan prestupne godine, tako da je 15 puta svaki ponedeljak i sreda.

Ciklus od 28 godina

Ako gledamo ponavljanje sudnjih dana u julijanskom 28-odnevnom ciklusu, postoji 1 prestupna godina i 3 neprestupne godine za svaki dan sedmice, neprestupne 6, 17, i 23 godine posle prestupne (sa intervalima od 6, 11, 6, i 5 godina; neravnomerno raspoređene jer posle 12 godina dan je preskočen u sekvenci sudnjih dana). Isti ciklus se može primeniti da bilo koji datum od 1. marta koji pada na određeni dan sedmice.

Za svaki zadati datum sve to 28. februara koji pada na određeni dan, 3 zajedničke godine su 5, 11, i 22 godine posle prestupne godine, sa intervalima 5, 6, 11 i 6 godina. Tako da je ciklus isti, ali sa petogodišnjim intervalom posle umesto pre prestupne godine.

Dakle, za svaki datum sem za 29. februar, intervali između neprustupnih godina koje padaju na određeni dan nedelje su 6, 11, 11.

Za 29. februar koji pada na određeni dan sedmice postoji samo jedan u svakih 28 godina, i naravno, prestupna je godina.

Julijanski kalendar

Gregorijanski kalendar precizno se ravna sa astronomskim dešavanjima kao što su ravnodnevnice, kratkodnevnice i dugodnevnice. Tokom 1582. se uvela ova modifikacija u Julijanoski kalendar. Da bi se ispravila greška u kalendaru, 10 dana su preskočeni, tako da je sudlji dan pomeren 10 dana unazad. Tabela uključuje godine Julijanskog kalendara, ali je algoritam za Gregorijanski i proleptični Gregorijanski kalendar.

Treba napomenuti da Gregorijanski kalendar nije prihvaćen u svim zemljama u istom trenutku, tako da za mnoge zemlje, različite regije su koristile različite datume za isti dan.

Potpuni primeri

Primer 1 (1985)

Pretpostavimo da znamo dan nedelje za 8. septembar 1985. godine. Počinjemo sa sidrom veka, sredom. Ovome ćemo dodati tri stvari, i zovemo ih a, b, c:

a je floor od 85/12, što je 7
b je 85 mod 12, što je 1
c je floor b/4 što je 0

Iz ovoga dobijamo da je a+b+c = 8. Brojimo 8 dana od srede, dolazimo da četvrtka, što jeste sudnji dan za 1985. godinu. Sada poredimo 18. septembar sa bliskim sudnjim danom, 5. septembrom. Vidimo da je 18. 13 dana od sudnjeg to jest jedan dan manje od dve nedelje.

Primer 2 (ostali vekovi)

Pretpostavimo da želimo da nađemo dan sedmice na koji je izbio Američki civilni rat, koji se desio 12. aprila 1861. Sidro za prošli vek je bilo 99 dana od četvrtka, ili, drugim rečima petak (izračunat kao (18 + 1) × 5 + ⌊18/4⌋; ili možemo samo da pogledamo u tabelu iznad, koja prikazuje sidra za vekove). Cifre 61 imaju razmak od 6 dana do sudnjeg dana, četvrtka. Dakle, 4. april je bio četvrtak, tako da je 12. aprili, 8 dana kasnije bio petak.

Reference

^ John Horton Conway, "Tomorrow is the Day After Doomsday", Eureka, volume 36, pages 28–31, October 1973.
^ Richard Guy, John Horton Conway, Elwyn Berlekamp : "Winning Ways: For Your Mathematical Plays, Volume. 2: Games in Particular", pages 795–797, Academic Press, London. 1982. ISBN 978-0-12-091102-8.
^ Carroll, Lewis (1887). „To Find the Day of the Week for any Given Date”. Nature. 35 (909): 517. Bibcode:1887Natur..35..517C. S2CID 4077610. doi:10.1038/035517a0.
^ Martin Gardner, "The Universe in a Handkerchief: Lewis Carroll's Mathematical Recreations, Games, Puzzles, and Word Plays", pages 24–26, Springer-Verlag, 1996
^ Alpert, Mark (1999). „Not Just Fun and Games”. Scientific American. 280 (4): 40—42. Bibcode:1999SciAm.280d..40A. doi:10.1038/scientificamerican0499-40.

Spoljašnje veze

Encyclopedia of Weekday Calculation by Hans-Christian Solka, 2010
Doomsday calculator that also "shows all work"
World records for mentally calculating the day of the week in the Gregorian Calendar
What is the day of the week, given any date?
Doomsday Algorithm
Finding the Day of the Week
„Poem explaining the Doomsday rule”. Arhivirano iz originala 18. 10. 2006. g. Pristupljeno 09. 01. 2016.

[1] John Horton Conway, "Tomorrow is the Day After Doomsday", Eureka, volume 36, pages 28–31, October 1973.

[2] Richard Guy, John Horton Conway, Elwyn Berlekamp : "Winning Ways: For Your Mathematical Plays, Volume. 2: Games in Particular", pages 795–797, Academic Press, London. 1982. ISBN 978-0-12-091102-8.

[3] Carroll, Lewis (1887). „To Find the Day of the Week for any Given Date”. Nature. 35 (909): 517. Bibcode:1887Natur..35..517C. S2CID 4077610. doi:10.1038/035517a0.

[4] Martin Gardner, "The Universe in a Handkerchief: Lewis Carroll's Mathematical Recreations, Games, Puzzles, and Word Plays", pages 24–26, Springer-Verlag, 1996

[5] Alpert, Mark (1999). „Not Just Fun and Games”. Scientific American. 280 (4): 40—42. Bibcode:1999SciAm.280d..40A. doi:10.1038/scientificamerican0499-40.

[1]

[2]

[3]

[4]

[5]