Problem umetničke galerije

Problem umetničke galerije ili problem muzeja je problem vidljivosti u računarskoj geometriji. Potiče iz problema čuvanja umetničke galerije sa minimalnim brojem stražara koji bez promene položaja mogu da nadgledaju čitavu galeriju. U računarskoj geometriji se prostorije umetničke galerije predstavljaju kao prost poligon, a svaki stražar je predstavljen tačkom u poligonu. Kaže se da skup tačaka $S$ čuva poligon ako za svaku tačku $p$ u poligonu postoji neko $q\in S$ tako da duž između $p$ i $q$ leži u unutrašnjosti poligona.

Primene problema umetničke galerije

Problem umetničke galerije pripada preseku robotike, optimizacije i računarske grafike, a vidljivost se sadrži u svim ovim poljima. Postoje brojne praktične primene kao što su postavljanje kamera u izlozima, raspored izvora svetlosti u sobi ili postavljanje radarskih stanica u planinskim predelima.

Raznolikosti u oblicima poligona su velika i globalno rešenje koje bi bilo dovoljno za sve tipove poligona još nije pronađeno. Ipak, u specijalnim slučajevima, ponuđena su raznovrsna rešenja problema umetničke galerije za određene tipove poligona.

U dve dimenzije

Originalni problem ima brojne varijacije koje takođe nose isti naziv. U nekim verzijama su stražari ograničeni na perimetar ili čak na temena poligona, dok druge verzije zahtevaju da samo perimetar ili neki njegov podskup bude pod nadzorom.

Rešavanje verzije u kojoj stražari moraju da se postave u temena, i samo temena treba da se čuvaju, ekvivalentno je rešavanju problema dominantnog skupa na grafu vidljivosti poligona.

Hvatalova teorema umetničke galerije

Hvatalova teorema umetničke galerije, nazvana po Vatslavu Hvatalu(Václav Chvátal), daje gornju granicu za minimalan broj stražara. Tvrdi se da je $\left\lfloor n/3\right\rfloor$ stražara uvek dovoljno, a nekada i neophodno, da čuva prost poligon sa $n$ temena.

Viktor Kli je 1973. godine prvi postavio pitanje o broju potrebnih temena ili stražara, a Hvatal ga je ubrzo dokazao. Hvatalov dokaz je kasnije uprostio Stiv Fisk preko argumenta 3-obojivosti.

Fiskov kratak dokaz

Fisk 1978. godine dokazuje teoremu umetničke galerije na sledeći način: Prvo se poligon $S$ trianguliše bez dodavanja novih temena. Svaka takva triangulacija ima bojenje sa tri boje $a,b,c$ . Neka je $T_{k}$ skup temena boje $a$ , i pretpostavljamo da $|T_{a}|\leq |T_{b}|\leq |T_{c}|$ . Ako kažemo da je $T=T_{k}$ iz toga sledi $|T|\leq n/3$ . Konačno, svaka tačka $q\in S$ se nalazi u nekom trouglu od $S$ , i svaki trougao od $S$ ima tačku $p\in T$ na njemu. Pošto su trouglovi konveksni, imamo da $pq\subset S$ .

Pošto tri boje dele $n$ temena poligona, boja sa najmanje temena čini ispravan skup stražara sa najviše $\left\lfloor n/3\right\rfloor$ stražara.

Generalizacije

Hvatalova gornja granica ostaje ispravna i ako promenimo problem tako da stražare, umesto samo u temenima, postavimo u bilo koju tačku koja pripada poligonu.

Postoji veliki broj drugih generalizacija i specijalizacija originalnog problema umetničke galerije koje model čine realističnijim i interesantnijim. Promene se dele na dve vrste: možemo menjati dozvoljene oblike koje može imati galerija ili možemo menjati sposobnosti i svrhu stražara.

Menjanje oblika galerije

Konveksan poligon
Ortogonalni poligon
Galerija sa rupom

Najjednostavniji poligon za ovaj problem, je konveksan poligon, pošto je u tom slučaju potreban samo jedan stražar koji se može nalaziti na bilo kojoj tački koja pripada poligonu.

Za ortogonalne poligone, čije ivice (zidovi) međusobno zaklapaju ugao od 90 stepeni, je potrebno samo $\lfloor n/4\rfloor$ čuvara. Za ovu teoremu postoje bar tri različita dokaza, od kojih nijedan nije jednostavan.^[1]^[2]

Galerije sa rupama. Pravimo model galerije tako što dopuštamo da se u unutrašnjosti galerije postave poligoni (rupe). Čuvari se ne smeju postavljati u unutrašnjosti rupa. Postavlja se osnovno pitanje minimalnog broja čuvara za galeriju sa $w$ zidova i $h$ rupa, gde se zidovi rupa takođe računaju kao zidovi galerije. Teorema daje gornju granicu za minimalan broj stražara u ovakvom modelu galerije i ona iznosi $\lfloor (w+h)/3\rfloor$ .^[3]

Menjanje sposobnosti stražara

U sličnom problemu se traži minimalan broj stražara koji mogu prekriti spoljašnjost poligona (“Problem tvrđave”). Za ovaj problem je $\lfloor n/2\rfloor$ stražara ponekada potrebno, a uvek dovoljno, što znači da je beskonačnu spoljašnjost teže prekriti od konačne unutrašnjosti.^[4] U problemu zatvorskog dvorišta, čuvari mogu biti postavljeni na ivicama poligona, i traži se da svaka tačka u ravni, kako unutar poligona tako i izvan njega, bude pod stražom. U suštini ovaj problem predstavlja spoj problema umetničke galerije za unutrašnjost poligona i problema tvrđave za njegovu spoljašnjost.

Računarska složenost

U verzijama problema odlučivanja problema umetničke galerije, kao ulaz su dati poligon i broj $k$ , i mora se izračunati da li dati poligon može biti prekriven sa $k$ ili manje čuvara. Ovaj problem i sve njegove standardne varijacije (kao što je na primer ograničavanje položaja čuvara na samo temena ili stranice) su NP-teške. Što se tiče aproksimacionih algoritama za određivanje minimalnog broja čuvara, Eidenbenc, Štam, i Videjer su 2001. godine dokazali da je problem aproksimaciono težak, što znači da je malo verovatno da se pomoću aproksimacionog algoritma polinomijalne složenosti može pronaći aproksimacioni odnos bolji od neke konstante. Međutim, konstantan aproksimacioni odnos nije otkriven. Umesto toga može se ostvariti logaritamska aproksimacija za minimalni broj stražara na temenima, i to svodeći problem na problem prekrivanja skupa. Kao sto je Valtr pokazao 1998. godine, skup dobijen iz problema umetničke galerije ima granične VC dimenzije i time omogućava korišćenje problema prekrivanja skupa zasnovanih na ε-mrežama čiji aproksimacioni odnos predstavlja logaritam optimalnog broja stražara, umesto broja temena poligona. Za neograničen broj stražara se pokazuje da potencijalno beskonačan broj pozicija dodatno komplikuje problem.

Međutim, postoje efikasni algoritmi za nalaženje skupa sa najviše $\lfloor n/3\rfloor$ temenih stražara, što se slaže sa Hvatalovom gornjom granicom. Dejvid Avis i Godfrid Tuseint su 1981. godine dokazali da se položaj ovih čuvara može izračunati u $O(nlogn)$ složenosti, u najgorem slučaju, koristeći podeli pa vladaj algoritam. Kušeš i Moret su 1992. godine napravili algoritam linearne složenosti koristeći Fiskov kratak dokaz i Bernand Šazeleov linearan algoritam za triangulaciju vremenske ravni.

Kouto, de Rezende i de Suza su 2011. godine predložili algoritam za temene stražare. Autori su izvršili opsežne eksperimente sa nekoliko klasa poligona i pokazali su da optimalna rešenja mogu biti pronađena za relativno kratko vreme izvršavanja, čak i za primere sa više od hiljadu temena. Ulazni podaci, kao i optimalna rešenja za ove primere, dostupni su na internetu.

Uopštenje u tri dimenzije

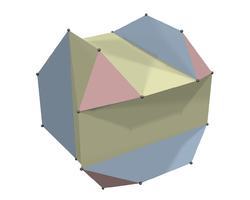
Ako je galerija predstavljena u tri dimenzije kao poliedar, onda stavljanje jednog stražara na svako teme ne bi garantovalo da će cela galerija biti pod nadzorom. Iako bi sve površine poliedra bile pod nadzorom, kod nekih poliedra postoje tačke u unutrašnjosti koje možda nisu pod nadzorom.

Reference

^ O'Rourke 1987, str. 31–80
^ Lubiw 1985;.
^ O'Rourke 1987, str. 125–145;.
^ O'Rourke 1987, str. 146–154

Literatura

Aggarwal, A. (1984), The art gallery theorem: Its variations, applications, and algorithmic aspects, Ph.D. thesis, Johns Hopkins University .
Avis, D.; Toussaint, G. T. (1981), „An efficient algorithm for decomposing a polygon into star-shaped polygons” (PDF), Pattern Recognition, 13 (6): 395—398, doi:10.1016/0031-3203(81)90002-9 .
Chvátal, V. (1975), „A combinatorial theorem in plane geometry”, Journal of Combinatorial Theory, Series B, 18: 39—41, doi:10.1016/0095-8956(75)90061-1 .
Couto, M.; de Rezende, P.; de Souza, C. (2011), Benchmark instances for the art gallery problem with vertex guards .
Eidenbenz, S.; Stamm, C.; Widmayer, P. (2001), „Inapproximability results for guarding polygons and terrains” (PDF), Algorithmica, 31 (1): 79—113, doi:10.1007/s00453-001-0040-8, Arhivirano iz originala (PDF) 24. 06. 2003. g., Pristupljeno 28. 01. 2016 .
Fisk, S. (1978), „A short proof of Chvátal's watchman theorem”, Journal of Combinatorial Theory, Series B, 24 (3): 374, doi:10.1016/0095-8956(78)90059-X .
Ghosh, S. K. (1987), „Approximation algorithms for art gallery problems”, Proc. Canadian Information Processing Society Congress, str. 429—434 .
Lee, D. T.; Lin, A. K. (1986), „Computational complexity of art gallery problems”, IEEE Transactions on Information Theory, 32 (2): 276—282, doi:10.1109/TIT.1986.1057165 .
Lubiw, A. (1985), „Decomposing polygonal regions into convex quadrilaterals”, Proc. 1st ACM Symposium on Computational Geometry, str. 97—106, ISBN 978-0-89791-163-4, doi:10.1145/323233.323247 .
O'Rourke, Joseph (1987), Art Gallery Theorems and Algorithms, Oxford University Press, ISBN 978-0-19-503965-8 .

Spoljašnje veze

[1] O'Rourke 1987, str. 31–80

[2] Lubiw 1985;.

[3] O'Rourke 1987, str. 125–145;.

[4] O'Rourke 1987, str. 146–154

[1]

[2]

[3]

[4]