Sabiranje Minkovskog

U geometriji zbir Minkovskog (takođe poznat kao dilacija) dva skupa pozicionih vektora A i V u Euklidovom prostoru formira se dodavanjem svakog vektora u A svakom vektoru u V tj skup

A+B=\{\mathbf {a} +\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}.

Analogno, razlika Minkovskog definiše se na sledeći način

A-B=\{\mathbf {a} -\mathbf {b} \,|\,\mathbf {a} \in A,\ \mathbf {b} \in B\}.

Primer

Na primer, ako imamo dva skupa A i V, pri čemu se svaki od njih sastoji iz tri poziciona vektora (neformalno rečeno, tri tačke), koji predstavljaju uglove dva trouglova u $\mathbb {R} ^{2}$ , sa koordinatama

A = {(1, 0), (0, 1), (0, -1)}

i

B = {(0, 0), (1, 1), (1, -1)}

,

onda je zbir Minkovskog $A + B = {(1, 0), (2, 1), (2, -1), (0, 1), (1, 2), (1, 0), (0, -1), (1, 0), (1, -2)}$ , što izgleda kao šestougao, sa tri 'ponovljene' tačke $(1, 0)$ .

Za zbir Minkovskog, nulti skup;{0}, koji sadrži samo nulti vektor 0, predstavlja neutralni element: za svaki podskup S vektorskog prostora

S + {0} = S;

Prazan skup je važan kod sabiranja Minkovskog zato što svaki prazan skup poništava svaki drugi podskup - za svaki drugi podskup S, vektorskog prostora, njegov zbir sa praznim skupom je prazan: $\emptyset$ .

Konveksni omotači zbira Minkovskog

Sabiranje Minkovskog ponaša se dobro u slučaju postupka uzimanja konveksnih omotača što je prikazano u sledećoj tvrdnji:

Za sve podskupove S₁ i S₂ realnog vektorskog prostora, konveksni omotač njihovih zbirova predstavlja zbir njihovih konveksnih omotača

Conv(S₁ + S₂) = Conv(S₁) + Conv(S₂).

Ovaj rezultat važi uopštenje za svaki konačni niz skupova koji nisu prazni

Conv(∑S_n) = ∑Conv(S_n).

U matematičkoj terminologiji, operacije sabiranja Minkovskog i formiranja konveksnih omotača predstavljaju operacije zamene.^[1]^[2]

Ako je $S$ konveksni skup $\mu S+\lambda S$ je konveksni set; onda

\mu S+\lambda S=(\mu +\lambda )S

za svaki

\mu ,\lambda \geq 0

.

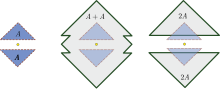
Obrnuto, ako ova „distributivna karakteristika" važi za sve realne brojeve koji nisu negativni, $\mu ,\lambda$ , onda je skup konveksan.^[3] Figura prikazuje primer nekonveksnog skupa za koji je $A + A \neq 2 A$ .

Primer nekonveksnog skupa tako da je $A + A \neq 2 A$

Sume Minkovskog se ponašaju linearno na spoljnoj liniji dvodimenzionalnih konveksnih tela: spoljna linija tog zbira jednaka je zbiru spoljnjih linija. Uz to, ako je K (unutrašnjost) kriva konstantne širine, onda je zbir K i njegove rotacije za 180 stepeni disk. Ove 2 činjenice mogu se kombinovati i dati kratak dokaz Barbijeve teoreme o spoljnim linijama konstantne sfere.^[4]

Primene

Sabiranje Minkovskog igra središnju ulogu u matematičkoj morfologiji. Ono se pojavljuje kod paradigme poteza 2D kompjuterske grafike (sa raznim primenama, naročito kod Donalda E.Knata u Megafontu), kao i kod operacije pomeranja tačaka kod čvrstog tela kod 3D kompjuterske grafike.

Planiranje kretanja

Zbirovi Minkovskog koriste se kod planiranja kretanja predmeta između prepreka. Koriste se za računanje konfiguracionih prostora, koji predstavljaju skup prisutnih pozicija predmeta. Kod prostornog modela translacionog kretanja jednog predmeta u avionu, gde pozicija predmeta može biti jedinstveno definisana pozicijom jedne fiksne tačke ovog predmeta, konfiguracioni prostor predstavljaja zbir Minkovskog skupa prepreka i pokretnog predmeta postavljenog na početku i rotiranog za 180 stepeni.

Numerička kontrola (NC) rada mašina

Kod numeričke kontrole rada mašina, programiranje NC alatke bazira se na činjenici da zbir Minkovskog alatke za sečenje sa njenom putanjom daje oblik isečku u materijalu.

Algoritmi za računanje Minkovskovog zbira

Primer u ravni

Dva konveksna mnogougla u ravni

Za dva konveksna mnogougla P i Q u ravni sa uglovima m i n, njihov zbir je jednak je konveksnom mnogouglu sa najviše m + n uglovima i može se izračunati u vremenu O (m + n) veoma jednostavnim postupkom, Pretpostavimo da su date ivice mnogougla. Pretpostavimo da su date ivice mnogougla, a smer je npr. u smeru kazaljke na satu duž granice mnogougla. Onda se lako vidi da ove ivice konveksnog mnogougla određuje ugao dvodimenzionalnog koordinatnog sistema. Hajde sad da ubacimo određene rasporede usmerenih ivica iz P i Q u jedan određeni raspored S. Zamislimo da su te ivice čvrste strelice koje se mogu slobodno kretari dok istovremeno idu paralelno svom prvobitnom pravcu. Sklopimo te strelice u red redosleda S vezujući kraj sledeće streliceza početak prethodne. Proizilazi da će rezultujući mnogougaoni lanac u stvari biti konveksni mnogougao koji je zbir Minkovskog P i Q.

Ostalo

Ako je jedan mnogougao konveksan, a drugi nije, kompleksnost njihovog zbira Minkovskog je O(nm). Ako su oba nekonveksna, kompleksnost njihovog zbira je O((mn)²).

Osnovni zbir Minkovskog

Postoji takođe i pojam osnovnog zbira Minkovskog +_e dva podskupa Euklidovog prostora. Uobičajeni zbir Minkovskog se može zabeležiti kao

A+B=\{z\in \mathbb {R} ^{n}\,|\,A\cap (\{z\}-B)\neq \emptyset \}.

Tako se osnovni zbir Minkovskog definiše ovako

A+_{\mathrm {e} }B=\{z\in \mathbb {R} ^{n}\,|\,\mu \left[A\cap (\{z\}-B)\right]>0\},

gde μ označava n-dimenzionalnu Lebeskovu meru. Razlog za termin "osnovni" leđi u sledećoj odlici indikatorske funkcije: dok je

1_{A\,+\,B}(z)=\sup _{x\,\in \,\mathbb {R} ^{n}}1_{A}(x)1_{B}(z-x),

može se videti kao

1_{A\,+_{\mathrm {e} }\,B}(z)=\mathop {\mathrm {ess\,sup} } _{x\,\in \,\mathbb {R} ^{n}}1_{A}(x)1_{B}(z-x),

gde "ess sup" označava osnovni supremum.

Reference

^ Theorem 3 (pages 562–563): Krein, M.; Šmulian, V. (1940). „On regularly convex sets in the space conjugate to a Banach space”. Annals of Mathematics (2), Second series. 41. str. 556—583. JSTOR 1968735. MR 2009. doi:10.2307/1968735.
^ For the commutativity of Minkowski addition and convexification, see Theorem 1.1.2 (pages 2–3) in Schneider; this reference discusses much of the literature on the convex hulls of Minkowski sumsets in its "Chapter 3 Minkowski addition" (pages 126–196): Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. str. xiv+490. ISBN 978-0-521-35220-8. MR 1216521.
^ Chapter 1: Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. str. xiv+490. ISBN 978-0-521-35220-8. MR 1216521.
^ The Theorem of Barbier (Java) at cut-the-knot.

Literatura

Arrow, Kenneth J.; Hahn, Frank H. (1980). General competitive analysis. Advanced textbooks in economics. 12 (reprint of (1971) San Francisco, CA: Holden-Day, Inc. Mathematical economics texts. 6 izd.). Amsterdam: North-Holland. ISBN 978-0-444-85497-1. MR 439057.
Gardner, Richard J. (2002), „The Brunn-Minkowski inequality”, Bull. Amer. Math. Soc. (N.S.), 39 (3): 355—405 (electronic), doi:10.1090/S0273-0979-02-00941-2
Green, Jerry; Heller, Walter P. (1981). „1 Mathematical analysis and convexity with applications to economics”. Ur.: Arrow, Kenneth Joseph; Intriligator, Michael D. Handbook of mathematical economics, Volume I. Handbooks in economics. 1. Amsterdam: North-Holland Publishing Co. str. 15—52. ISBN 978-0-444-86126-9. MR 634800. doi:10.1016/S1573-4382(81)01005-9. Arhivirano iz originala 17. 12. 2012. g. Pristupljeno 15. 05. 2014.
Mann, Henry (1976), Addition Theorems: The Addition Theorems of Group Theory and Number Theory (Corrected reprint of 1965 Wiley izd.), Huntington, New York: Robert E. Krieger Publishing Company, ISBN 978-0-88275-418-5 Spoljašnja veza u |publisher= (pomoć)
Rockafellar, R. Tyrrell (1997). Convex analysis. Princeton landmarks in mathematics (Reprint of the 1979 Princeton mathematical series 28 izd.). Princeton, NJ: Princeton University Press. str. xviii+451. ISBN 978-0-691-01586-6. MR 1451876. MR 274683.
Nathanson, Melvyn B. (1996), Additive Number Theory: Inverse Problems and Geometry of Sumsets, GTM, 165, Springer, Zbl 0859.11003 .
Oks, Eduard; Sharir, Micha (2006), „Minkowski Sums of Monotone and General Simple Polygons”, Discrete and Computational Geometry, 35 (2): 223—240, doi:10.1007/s00454-005-1206-y .
Schneider, Rolf (1993), Convex bodies: the Brunn-Minkowski theory, Cambridge: Cambridge University Press .
Tao, Terence & Vu, Van (2006), Additive Combinatorics, Cambridge University Press .

Šablon:Functional Analysis

[1] Theorem 3 (pages 562–563): Krein, M.; Šmulian, V. (1940). „On regularly convex sets in the space conjugate to a Banach space”. Annals of Mathematics (2), Second series. 41. str. 556—583. JSTOR 1968735. MR 2009. doi:10.2307/1968735.

[Schneider-2] For the commutativity of Minkowski addition and convexification, see Theorem 1.1.2 (pages 2–3) in Schneider; this reference discusses much of the literature on the convex hulls of Minkowski sumsets in its "Chapter 3 Minkowski addition" (pages 126–196): Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. str. xiv+490. ISBN 978-0-521-35220-8. MR 1216521.

[automatski_generisano1-3] Chapter 1: Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. str. xiv+490. ISBN 978-0-521-35220-8. MR 1216521.

[4] The Theorem of Barbier (Java) at cut-the-knot.

[1]

[2]

[3]

[4]