Sedam mostova Kenigsberga
Appearance
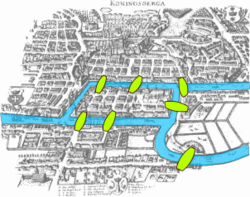
Sedam mostova Kenigsberga je matematički problem kojim se u 18. veku bavio Leonard Ojler. On je 1736. dokazao da je problem nemoguće rešiti i na taj način postavio osnove teorije grafova i postao začetnik ideje o topologiji.[1][2]
Problem je zadat na sledeći način: „Da li je moguće preći svih sedam mostova grada tako da se vrati na početak puta, ali da se svaki most pređe samo jedanput?”
On je prikazao mapu mostova gde je kopno prikazao kao čvorove grafa, a mostove kao grane između njih. Zaključio je da rešenje ne postoji, odnosno da na ovakav način nije moguće preći mostove. Razlog je bio to što graf mora da ima nula ili dva čvora parnog stepena (broj grana koje ulaze ili izlaze iz čvora).
Vidi još
[uredi | uredi izvor]Reference
[uredi | uredi izvor]- ^ Euler, Leonhard (1736). "Solutio problematis ad geometriam situs pertinentis". Comment. Acad. Sci. U. Petrop 8, 128–40.
- ^ Shields, Rob (decembar 2012). „Cultural Topology: The Seven Bridges of Königsburg 1736”. Theory, Culture & Society. 29 (4–5): 43—57. doi:10.1177/0263276412451161. Shields provides a discussion of the social significance of Euler's engagement with this popular problem and its significance as an example of (proto-)topological understanding applied to everyday life.
Spoljašnje veze
[uredi | uredi izvor]- Leonard Euler's Solution to the Konigsberg Bridge Problem Arhivirano na veb-sajtu Wayback Machine (23. jun 2020)
- The Bridges of Königsberg


