Usmereni graf

Usmereni graf.

Usmereni graf sa odgovarajućom matricom susedstva

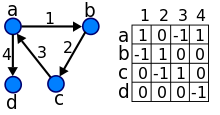
U matematici, a posebno u teoriji grafova, usmereni graf ili digraf je graf ili skup čvorova povezanih granama, gde grane imaju pravac. U formalnom smislu, usmeren graf-to je uređen par G = (V, A) (ponekad u oznaci G = (V, E)).

• V je  skup čiji se elementi zovu vrhovi, čvorovi, ili tačke;
• A(ponekad i E) je skup uređenih parova čvorova, koje se nazivaoju strelicama, usmerenim granama (ponekad samo granama sa odgovarajućim skupom po imenu E umesto A),ili usmerene linije.

On se razlikuje od običnog ili neusmerenog grafa, u tome što je neusmereni graf definisan kao skup dvoelementnih skupova čvorova, koji se obično nazivaju grane ili linije.

Usmereni graf se zove prost digraf , ako između nikoja dva različita čvora ne postoji više od jedne usmerene grane i ako nema petlje (grane koje povezuju čvor sa samim sobom). Usmereni graf se zove usmereni multigraf ili multidigraf ako on može da ima nekoliko strela (a ponekad i cikluse). U ovom drugom slučaju, grane formiraju multiskup, a ne skup, uređenih parova čvorova.

Osnovni pojmovi

Grana (x,y) smatra se usmerenom od čvora x do čvora y; Y se zove glava a x se zove rep grane (strelice); Y je direktan sledbenik od x-a,  a x je direktan prethodnik od y. Ako put vodi od x-a ka y kod, y je sledbenik od x i dostižan (moguće je stići do tog čvora) od x. X je prethodnik y-a. Grana (y,x) se zove obrnutom granom (x,y).

Dodajući orijentaciju neodređenom grafu, tj postavljajuči smer svake grane, od običnog grafa dobijamo usmeren graf. Bilo koji graf koji se napravi na ovakav način naziva se orijentisan graf. Među usmerenim grafovima, orijentisajni grafovi su oni koji nemaju 2 ciklusa (najviše jedna grana (x,y) i jedna grana (y,x) mogu biti grane grafa).

Težinski usmereni graf je usmereni graf sa određenim težinama (vrednostima) koje se dodaju uz svaku granu, sličan je kao težinski graf.

U kontekstu teorije grafova, težinski usmereni graf se često nazivamrežom.

Matrica susedstva multidigrafa koji ima cikluse, je matrica sa celim vrednostima, redovima i kolonama koji odgovaraju čvorovima, gde je nedijagonalno polje a_ij - broj grana od čvora i do čvora j, a dijagonalno poljea_ii - broj ciklusa u čvoru i.

Još jedno matrično prikazivanje grafa je njegova matrica učestalosti.

Ulazni i izlazni stepen

Usmereni graf, sa označenim čvorovima (ulazni stepen, izlazni stepen).

Ulazni stepen čvora (u)  u oznaci deg-(u) predstavlja broj grana kojima je čvor u završni čvor. Izlazni stepen čvora (u) u oznaci deg+(u) predstavlja broj grana kojima je čvor u početni čvor.

Neka je G = (V, E) i v∈V. Čvor koji ima deg-(u)=0 naziva se izvorom, i on je poreklo svih ostalih incidentnih grana.

Slično tome, čvor koji ima deg+(v)=0 naziva se ponor.

Ako čvor nije ni izvor , ni ponor, tada se on zove unutrašnji.

Formula za stepen čvora u usmerenom grafu je

${\displaystyle }$

Ako za svaki čvor važi v∈V, deg+(v) = deg−(v), tada se taj graf naziva balansiran orijentisan graf.

Niz stepena

Niz stepena direktnog grafa je niz parova, njegovih ulaznih i izlaznih stepena, za primer koji je gore naveden, imamo niz stepena ((2, 0), (2, 2), (0, 2), (1, 1)). Dva grafa su izomorfna ako imaji isti niz stepena, mada ponekad se može desiti da grafovi iako nisu izomorfni imaju isti niz stepena

Problem realizacije grafa je zadatak pronalaženja usmerenog grafa sa zadatim nizom stepena koji su dati u obliku celobrojnih parova. Niz, koji je niz stepena nekog usmerenog grafa, odnosno za koji problem realizacije usmerenog grafa ima rešenje, zove se usmereni graf ili usmeren grafički niz. Ovaj problem može biti rešen uz pomoć Kleitman–Van algoritma ili uz pomoć Fulkerson–Čen–Anstee teoreme.

Povezanost usmerenog grafa

Usmeren graf je slabo povezan (ili samo povezan), ako je neusmeren osnovni graf, dobijen zamenom svih grana u direktnom grafu sa neusmerenim granama,povezan graf. Usmeren graf je jako povezan ili jak, ako sadrži direktan put iz u čvor y, i direktan put iz čvora y do čvora x, za svaki par čvorova (x,y). Jake komponente su najjači povezani podgrafovi.

Klase usmerenog grafa

Simetrični digraf je usmereni graf u kome svaka grana koja njemu pripada, ima svoju inverznu granu, koja takođe njemu pripada. Simetričan, bezcikličan usmeren je ekvivalentan grafu sa granama zamenjenim sa parom inverznih grana. Broj neusmerenih grana je jednak polovini broju usmerenih grana.

Jednostavan orijentisan acikličan graf.

Usmeren acikličan graf je usmeren graf bez usmerenih ciklusa. Poseban slučaj usmerenih acikličnih grafova, su  multistabla (grafovi u kojima ne postoji put tako da se iz početnog čvora vrati nazad do tog istog čvora), orijentisano stablo ili polistablo (usmereni grafovi dobijeni usmeravanjem svih grana neusmerenog acikličnog stabla) i korenovo stablo (orijentisane stablo, u kome je jedan čvor označen kao koren, tj početan čvor).

Turnir na 4 vrha.

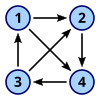
Turnir - je orijentisan graf dobijen tako što se bira smer svake grane u neusmerenom potpunom grafu.

Vidi još

• Dijagram toka
• Teorija grafova
• Graf toka (matematika)
• Orijentacija (teorija grafova)
• Signalni tok grafa
• Vertikalno ograničen graf

Literatura

• Bang-Jensen, Jørgen; Gutin, Gregory (2000). directed graphs: Theory, Algorithms and Applications. Springer. ISBN 978-1-85233-268-6. 
  (revidiran 1-og izdanja 2007. godine, sada slobodno dostupan na autora sajta; 2. izdanje pojavio u 2009, ISBN 1-84800-997-6).
• Bondy, John Adrian; Murty, U. S. R. (1976). Graph Theory with Applications. North-Holland. ISBN 978-0-444-19451-0. Arhivirano iz originala 13. 04. 2010. g. Pristupljeno 25. 06. 2016. .
• Diestel, Reinhard (2005). Graph Theory (3rd izd.). Springer. ISBN 978-3-540-26182-7.  (elektronski 3. izdanje je slobodno dostupan na sajtu autora).
• Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley .
• Broj cilju tačkama (ili grafa) sa vrhova od onlajn Enciklopedije Integer sekvenci