Hemingovo rastojanje
 |
 |
 | |
 | |
U teoriji informacija, Hemingovo rastojanje između dve niske (reči) jednakih dužina je jednako broju mesta na kojima se odgovarajući simboli tih niski ne poklapaju. Drugim rečima, Hemingovo rastojanje predstavlja minimalan broj zamena koje je neophodno sprovesti da bi se jedna niska pretvorila udrugu, ili broj grešaka koje su transformisale jednu nisku u drugu.
Primeri
[uredi | uredi izvor]Hemingovo rastojanje između:
- "tačka" i "bačva" je 2.
- 1011101 i 1001001 je 2.
- 2173896 i 2233796 je 3.
Specijalna svojstva
[uredi | uredi izvor]Za fiksnu dužinu n, Hemingovo rastojanje je metrika na vektorskom prostoru reči te dužine, jer očigledno ispunjava svojstva nenegativnosti, važi da je H(x, y) = 0 akko x = y, ispunjava svojstvo simetrije, i lako se može pokazati potpunom indukcijom da zadovoljava i svojstvo nejednakosti trougla. Hemingovo rastojanje između reči a i b može takođe da se posmatra i kao Hemingova težina za a−b uz odgovarajući izbor operatora −.
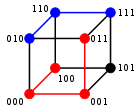
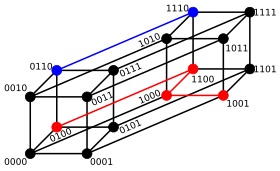
Kad su u pitanju binarne niske a i b Hemingovo rastojanje je jednako broju jedinica u a XOR b. Metrički prostor binarnih niski dužine n, sa Hemingovim rastojanjem je poznat kao Hemingova kocka; ona je kao metrički prostor ekvivalentna skupu čvorova u grafu u obliku hiperkocke. Binarne niske dužine n mogu da se posmatraju i kao vektor u gde se svaki simbol posmatra kao realna koordinata; na ovaj način, niske daju čvorove n-dimenzione hiperkocke, a Hemingovo rastojanje između dve niske je ekvivalentno Menhetn rastojanju između čvorova.
Istorija i primene
[uredi | uredi izvor]Hemingovo rastojanje je nazvano po Ričardu Hemingu, koji ga je uveo u svom radu o Hemingovom kodu, Kodiranja za otkrivanje i korekciju grešaka iz 1950. godine.[1] Koristi se u telekomunikacijama gde broj zamenjenih bitova u binarnoj reči fiksne dužine predstavlja procenu greške, i stoga se ponekad naziva signalno rastojanje. Analiza Hemingove težine se koristi u više disciplina uključujući teoriju informacija, teoriju kodiranja, i kriptografiju. Međutim, za upoređivanje niski različitih dužina, ili niski gde se ne očekuju samo zamene simbola već i njihovo umetanje ili brisanje, od veće koristi su sofisticiranije metrike, poput Levenštajnovog rastojanja. Za q-arne niske nad azbukom veličine q ≥ 2 Hemingovo rastojanje se primenjuje u slučaju ortogonalne modulacije, dok se Lijevo rastojanje koristi za faznu modulaciju. Ako je q = 2 ili q = 3 ova dva rastojanja se poklapaju.
Hemingovo rastojanje se takođe koristi u sistematici, kao mera genetskog rastojanja.[2]
Na mreži (poput šahovske table), tačke na Lijevom rastojanju 1 grade fon Nojmanovu okolinu oko te tačke.
Primer algoritma
[uredi | uredi izvor]Pajton funkcija hamming_distance() računa Hemingovo rastojanje između dve niske (ili drugih iterabilnih objekata) jednake dužine, tako što napravi niz nula i jedinica koje označavaju poklapanja ili nepoklapanja između odgovarajućih pozicija u dve niske, i zatim sabere elemente tog niza.
def hamming_distance(s1, s2):
assert len(s1) == len(s2)
return sum(ch1 != ch2 for ch1, ch2 in zip(s1, s2))
Sledeća C funkcija računa Hemingovo rastojanje dva cela broja (posmatrana u binarnom obliku, to jest kao niz bitova). Vreme izvršavanja ove procedure je proporcionalno Hemingovom rastojanju dva broja a ne broju bitova u ulazu. Računa se bitovska ekskluzivna disjunkcija dva zadata broja, a zatim se nalazi Hemingova težina rezultata (broj bitova različitih od nule) korišćenjem algoritma[3] koji uzastopno pronalazi i briše bit različit od nule najnižeg reda.
unsigned hamdist(unsigned x, unsigned y)
{
unsigned dist = 0, val = x ^ y;
// Count the number of set bits
while(val)
{
++dist;
val &= val - 1;
}
return dist;
}
Vidi još
[uredi | uredi izvor]Napomene
[uredi | uredi izvor]- Ovaj članak uključuje materijal iz dokumenta Federalni standard 1037C (Federal Standard 1037C), Administracije za opšte službe (General Services Administration). Ovaj dokument je u javnom vlasništvu.
- ^ (PDF). 26 (2): 147—160 https://web.archive.org/web/20060525060427/http://www.caip.rutgers.edu/~bushnell/dsdwebsite/hamming.pdf. Arhivirano iz originala (PDF) 25. 05. 2006. g. Pristupljeno 14. 05. 2010. Nedostaje ili je prazan parametar
|title=(pomoć), MR0035935, http://www.caip.rutgers.edu/~bushnell/dsdwebsite/hamming.pdf Arhivirano na sajtu Wayback Machine (25. maj 2006) . - ^ Pilcher, C. D.; Wong, J. K.; Pillai, S. K. (2008). „Inferring HIV transmission dynamics from phylogenetic sequence relationships”. PLOS Medicine. 5 (3): e69. PMC 2267810
 . PMID 18351799. doi:10.1371/journal.pmed.0050069
. PMID 18351799. doi:10.1371/journal.pmed.0050069  .
.
- ^ Wegner, Peter (1960). „A technique for counting ones in a binary computer”. Communications of the ACM. 3 (5): 322. S2CID 31683715. doi:10.1145/367236.367286..
Spoljašnje veze
[uredi | uredi izvor]- Primer Hemingovog rastojanja (jezik: engleski)
- Alat za pravljenje Hemingovog koda (jezik: engleski)

