Kolpicov oscilator
Овај чланак можда захтева чишћење и/или прерађивање како би се задовољили стандарди квалитета Википедије. |
Kolpicov oscilator je izmislio američki inženjer Edvin H. Kolpits 1920. U pitanju je jedan od mnogobrojnih oscilatora realizovanih pomoću kalema i kondenzatora koji služe za kontrolu frekvencije i često se još naziva LC oscilator.
Ocilatori u tri tačke
[уреди | уреди извор]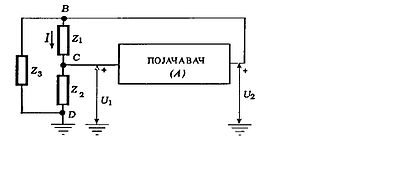
Oscilatori u tri tačke sadrže pojačavač i kolo povratne sprege. Kolo povratne sprege je priključeno na tri tačke pojačavača kao na slici: izlaz (tačka B), ulaz (tačka C) i masu (tačka D).
Opšti uslovi oscilovanja proizilaze iz sledećeg objašnjenja: pojačavač se obično sastoji od jednog pojačavačkog stepena sa fetom (sa zajedničkim izvorom) ili sa bipolarnim tranzistorom (sa zajedničkim emitorom). Ovakav pojačavač normalno pomera fazu sa 180˚. Da bi ukupan fazni pomeraj bio 360˚, kolo povratne sprege treba da je pomeri za još 180˚. Povratna sprega se kod ovakvih oscilatora ostvaruje preko oscilatornog kola, koje je na slici predstavljeno preko impendansi Z1, Z2 i Z3. Povratna sprega se ostvaruje preko impendasni Z1 i Z2, a Z3 služi da se obrazuje paralelno oscilatorno kolo.
Koeficijent povratne sprege je jednak:
- β = U1/U2 = Z2I/(Z1+Z2)I = Z2/(Z1+Z2) (1)
Impendanse su obično reaktivne, pa umesto Z1 može da se piše X1, umesto Z2 može da se piše X2, a X3 umesto X3. Kada se ove vrijednosti zamene u jednačini (1) dobija se:
- β = X2/(X1+X2) (2)
Da bi koeficijent kola povratne sprege bio negativan, odnosno da bi pomeraj faze bio 180˚, reaktanse X1 i X2 moraju imati različite predznake i moduo reaktanse X1 mora biti veći od modula reaktanse X2. To znači ako je reaktansa X1 induktivna, reaktansa X2 će biti kapacitivna, a mora biti X1 | > | X2 |.
Na rezonatnoj učestanosti zbir reaktansi unutar oscilatornog kola mora biti jednak nuli:
- X1+X2+X3 = 0 (3)
Ako je reaktansa X1 jednog znaka (npr. pozitivna, tj. induktivna), rektanse X2 i X3 moraju biti negativne tj. kapacitivne. Iz jednačine (3) dobija se:
- X1+X2 = -X3 (4)
Ako se ova vrijednost zameni u jednačinu (2) dobija se:
- β = X2/-X3 (5)
Ako je reaktansa X1 induktivna, a X2 i X3 kapacitivne onda imamo Kolpicov oscilator. Još jedino treba da se zadovolji uslov da pojačanje pojačavača bude jednako slabljenju kola povratne sprege odnosno da se zadovolji uslov β A | = 1. Reaktanse se mogu odabrati tako da čitavo kolo uopšte nema slabljenje pa tada mogu da se upotrebe pojačavači sa malim pojačanjem (većim od 1).
Kolpicov osilator sa fetom
[уреди | уреди извор]Kolpicov oscilator sa fetom je prikazan na slici 2. Fet sa elementima Rd, Rs i Cs čini pojačavač sa zajedničkim sorsom, čije je naponsko pojačanje relativno malo. Povratna sprega se ostvaruje preko oscilatornog kola, koje se sastoji od kalema L i kondenzatora C1 i C2. Na slici se vidi da je jedna tačka oscilatornog kola priključena na izlaz pojačavača ( tačka B ), druga na njegov ulaz ( tačka C ) i treća na masu ( tačka D ).
Obrtanje faze kod Kolpicovog oscilatora. Učestanost oscilovanja.
[уреди | уреди извор]Trebalo bi objasniti kako se obrće faza kod Kolpicovog oscilatora za 180˚ od tačke B do tačke C u odnosu na masu. Ako se jednačina (5) primeni na sliku 2, za slabljenje kola povratne sprege može da se napiše:
- 1/β = U2/U1 = -X3/X2 = -1/ωC1/1/ωC2 = -C2/C1 (6)
Iz jednačine (6) se vidi da je koeficijent povratne sprege negativan što znači da mu je fazni pomeraj 180˚. Ako su kapacitivnosti C1 i C2 jednake, slabljenje kola je jednako jedinici odnosno nema slabljenja, pa je dovoljno da pojačanje pojačavača bude nesto veće od 1.
Učestanost oscilovanja se određuje iz jednačine (3) gde treba umesto X1 staviti ωL, umesto X2 staviti -1/ωC2 a umesto X3 -1/ωC1 pa se dobije:
- ωL – (1/ω) (1/C2 + 1/C1) = ωL – 1/(ωCu) = 0 (7)
Odavde učestanost oscilovanja je jednaka:
- ω2 = 1/(LCu) tj. f 2 = 1/(4π2LCu) (8)
Ekvivalentna kapacitivnost je jednaka rednoj vezi kondenzatora C1 i C2.

Izlazna otpornost kod Kolpicovog oscilatora
[уреди | уреди извор]Kod Kolpicovog oscilatora je veoma važno da izlazna otpornost pojačavača bude što veća jer je na njegov izlaz priključeno paralelno oscilatorno kolo. Izlazna otpornost pojačavača na slici 2 je približno jednaka otpornosti Rd koja kod normalnih pojačavača iznosi nekoliko kΩ. Ovako mala izlazna otpornost bi prigušivala oscilatorno kolo, pa se ovde uzima nesšto veča vrednost za Rd (10 do 30 kΩ ). Tada je struja drejna mala (npr. 50 μA ) i treba takođe staviti veču otpornost Rs u kolo sorsa ( npr. 5 kΩ ) da bi se dobio dovoljan automatski pednapon UGS. Izlazna impendansa pojačavača se može povećati stavljanjem male kapacitivnosti na mesto Cs1. Ponekad se umesto kondenzatora Cs1 stavlja otpornik (obično 100 kΩ) da bi prigušenje oscilatornog kola bilo što manje i jednako na svim učestanostima. Što je prigušenje oscilatornog kola manje to je njegova selektivnost veća, a takođe je veča stabilnost učestanosti. Ponekad se umesto otpornika Rd stavlja prigušnica ( kalem velike induktivnosti ). Njena impendansa je na visokim učestanostima obično veća od otpornosti Rd ali je zato to mnogo skuplje rešenje.
Upotreba i karakteristike
[уреди | уреди извор]Videli smo da su kondenzatori C1 i C2 obično jednaki. Ako je potrebno kontinualno menjati učestanost, tada se upotrebljavaju 2 ista promenljiva kondenzatora na istoj osovini, koji se inače proizvode za potrebe radio-industrije. Nije pogodno menjati samo jednu kapacitivnost jer bi se tako menjalo slabljenje kola povratne sprege, pa bi se moglo desiti da izlazni napon bude suviše izobličen ili da oscilovanje prestane. I ovde se kapacitivnosti normalno menjaju u odnosu 1:10 a učestanosti 3,16:1.
Kolpicov oscilator se može upotrebiti u vrlo širokom opsegu učestanosti, kao na primer od 100kHz do 300MHz, sa istim kondenzatorima uz promenu kalema. Iznad 300MHz bi se kalem sveo na samo jedan navojak, pa bi bilo teško kontrolisati i stabilizovati učestanost. Ovaj tip oscilatora obično ima jako izobličen sinusni napon na izlazu pojačavača. Izobličen napon sadrži pored sinusnog napona osnovne učestanosti, takođe i sinusne napone viših učestanosti koje su 2,3.. puta više od osnovne. Izobličenje je znatno manje na ulazu pojačavača, jer se između tačke C na slici 2 i mase nalazi kondenzator C2. On je praktično kratak spoj za više harmonike, čija je učestanost nekoliko puta viša od osnovne učestanosti oscilovanja.
Kolpicov oscilator sa bipolarnim tranzistorima
[уреди | уреди извор]
Kolpicov oscilator takođe može da se izvede preko bipolarnih tranzistora kao što je prikazano na slici 3. Princip rada ovog oscilatora je isti kao kod onog na slici 2, samo je ovde manja otpornost ulaznog pojačavača. Da bi se dobila veća ulazna otpornost ponekad se izostavlja kondenzator Ce. I ovde se može umesto otpornika Rc staviti prigušnica što je znatno skuplje rešenje.
Референце
[уреди | уреди извор]Литература
[уреди | уреди извор]- Ulrich L. Rohde, Ajay K. Poddar, Georg Böck, The Design of Modern Microwave Oscillators for Wireless Applications : Theory and Optimization, John Wiley & Sons, New York, NY, May. 2005. ISBN 978-0-471-72342-4.
- George Vendelin, Anthony M. Pavio, Ulrich L. Rohde " Microwave Circuit Design Using Linear and Nonlinear Techniques ", John Wiley & Sons, New York, NY, May. 2005. ISBN 978-0-471-41479-7.
