Štrasenov algoritam

Štrasenov algoritam, koji je dobio ime po nemačkom matematičaru Volkeru Štrasenu, služi za množenje matrica. Brži je od standardnog algoritma za množenje matrica i koristi se za matrice velikog stepena, međutim postoje algoritmi koji su još brži za veoma velike matrice.

Istorija

Volker Štrasen je ovaj algoritam objavio 1969. godine i dokazao da za n³ standardni algoritam nije optimalan. Štrasenov algoritam nije puno bolji, ali je prouzrokovao intezivnije istraživanje na temu množenja matrica što je dovelo do bržih algoritama kao što je Coppersmith–Winograd algoritam.

Algoritam

Shematski prikaz Štrasenovog algoritma

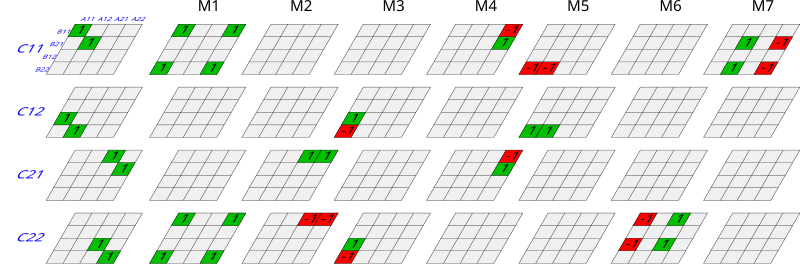
Neka su A i B kvadratne matrice nad R. Mi želimo da izračunamo njihov proizvod što će biti matrica C:

$\mathbf {C} =\mathbf {A} \mathbf {B} \qquad \mathbf {A} ,\mathbf {B} ,\mathbf {C} \in R^{2^{n}\times 2^{n}}$

Ako A i/ili B nisu tipa $2^{x}\times 2^{x}$ popunimo redove i kolone koji nedostaju nulama.

Podelimo A, B i C u blokove jednakih dimenzija:

$\mathbf {A} ={\begin{bmatrix}\mathbf {A} _{1,1}&\mathbf {A} _{1,2}\\\mathbf {A} _{2,1}&\mathbf {A} _{2,2}\end{bmatrix}}{\mbox{ , }}\mathbf {B} ={\begin{bmatrix}\mathbf {B} _{1,1}&\mathbf {B} _{1,2}\\\mathbf {B} _{2,1}&\mathbf {B} _{2,2}\end{bmatrix}}{\mbox{ , }}\mathbf {C} ={\begin{bmatrix}\mathbf {C} _{1,1}&\mathbf {C} _{1,2}\\\mathbf {C} _{2,1}&\mathbf {C} _{2,2}\end{bmatrix}}$

tako da važi:

$\mathbf {A} _{i,j},\mathbf {B} _{i,j},\mathbf {C} _{i,j}\in R^{2^{n-1}\times 2^{n-1}}$

onda je:

$\mathbf {C} _{1,1}=\mathbf {A} _{1,1}\mathbf {B} _{1,1}+\mathbf {A} _{1,2}\mathbf {B} _{2,1}$

$\mathbf {C} _{1,2}=\mathbf {A} _{1,1}\mathbf {B} _{1,2}+\mathbf {A} _{1,2}\mathbf {B} _{2,2}$

$\mathbf {C} _{2,1}=\mathbf {A} _{2,1}\mathbf {B} _{1,1}+\mathbf {A} _{2,2}\mathbf {B} _{2,1}$

$\mathbf {C} _{2,2}=\mathbf {A} _{2,1}\mathbf {B} _{1,2}+\mathbf {A} _{2,2}\mathbf {B} _{2,2}$

Ovim nismo smanjili broj množenja. Još uvek nam treba 8 množenja da bismo odredili C_i,j matrice.

Sledi najvažniji deo. Definišemo nove matrice:

$\mathbf {M} _{1}:=(\mathbf {A} _{1,1}+\mathbf {A} _{2,2})(\mathbf {B} _{1,1}+\mathbf {B} _{2,2})$

$\mathbf {M} _{2}:=(\mathbf {A} _{2,1}+\mathbf {A} _{2,2})\mathbf {B} _{1,1}$

$\mathbf {M} _{3}:=\mathbf {A} _{1,1}(\mathbf {B} _{1,2}-\mathbf {B} _{2,2})$

$\mathbf {M} _{4}:=\mathbf {A} _{2,2}(\mathbf {B} _{2,1}-\mathbf {B} _{1,1})$

$\mathbf {M} _{5}:=(\mathbf {A} _{1,1}+\mathbf {A} _{1,2})\mathbf {B} _{2,2}$

$\mathbf {M} _{6}:=(\mathbf {A} _{2,1}-\mathbf {A} _{1,1})(\mathbf {B} _{1,1}+\mathbf {B} _{1,2})$

$\mathbf {M} _{7}:=(\mathbf {A} _{1,2}-\mathbf {A} _{2,2})(\mathbf {B} _{2,1}+\mathbf {B} _{2,2})$

Sada možemo izraziti C_i,j preko M_k:

$\mathbf {C} _{1,1}=\mathbf {M} _{1}+\mathbf {M} _{4}-\mathbf {M} _{5}+\mathbf {M} _{7}$

$\mathbf {C} _{1,2}=\mathbf {M} _{3}+\mathbf {M} _{5}$

$\mathbf {C} _{2,1}=\mathbf {M} _{2}+\mathbf {M} _{4}$

$\mathbf {C} _{2,2}=\mathbf {M} _{1}-\mathbf {M} _{2}+\mathbf {M} _{3}+\mathbf {M} _{6}$

Prolazimo kroz algoritam n puta (dok podmatrice ne postanu brojevi). Na kraju treba obrisati preostale nule.

Obično se pri implementiranju Štrasenovog algoritma za dovoljno male podmatrice koriste standardne metode, koje su u tom slučaju efikasnije. Prelazna tačka na kojoj Štrasenov algoritam postaje efikasniji zavisi od implementacije i hardvera. Ranije se predviđalo da je Štrasenov algoritam brži kod matrica dimenzija između 32 i 128 za optimizovane implementacije. Međutim u skorije vreme se ispostavilo da se prelazna tačka povećava, istraživanje sprovedeno 2010. godine pokazalo je da na trenutnim arhitekturama čak ni samo jedan korak Štrasenovog algoritma ne donosi prednosti u odnosu na optimizovana tradicionalna množenja, dok rang matrica ne pređe 1000, pa čak i tad, kada je rang do nekoliko hiljada, prednost je marginalna (u najboljem slučaju 10%).

Asimptotska složenost

Standardno množenje matrica ima približno 2N³ (za N = 2ⁿ) aritmetičkih operacija; asimptotska složenost je Θ(N³).

Broj aritmetičkih operacija u Štrasenovom algoritmu može da se izračuna na sledeći način: neka je f(n) broj operacija za matricu dimenzije 2ⁿ × 2ⁿ. Zatim rekurzivnom primenom algoritma, vidimo da je f(n) = 7f(n−1) + l4ⁿ, za neko konstantno ''l koje zavisi od broja sabiranja u konkretnoj implementaciji algoritma. Dakle f(n) = (7 + o(1))n, t.j. asimptotska složenost za množenje matrica dimenzije N = 2n pomoću Štrasenovog algoritma je:

$O([7+o(1)]^{n})=O(N^{\log _{2}7+o(1)})\approx O(N^{2.8074})$.

Umanjenjem broja aritmetičkih operacija se ipak smanjuje numerička stabilnost, takođe algoritam zahteva znatno više memorije u odnosu na naivni algoritam. Dimenzije obe početne matrice treba proširiti do prvog sledećeg stepena dvojke, što može povećati broj elemenata do četiri puta i rezultovati sa sedam pomoćnih matrica takvih da svaka ima četvrtinu elemenata iz proširenog dela.

Rang ili bilinearna složenost

Bilinearna složenost ili rang bilinearne mape je bitan koncept u asimptotskoj složenosti množenja matrica. Rang bilinearne mape $\phi :\mathbf {A} \times \mathbf {B} \rightarrow \mathbf {C}$ nad poljem F se definiše kao (ne baš formalna notacija):

$R(\phi /\mathbf {F} )=\min \left\{r\left|\exists f_{i}\in \mathbf {A} ^{*},g_{i}\in \mathbf {B} ^{*},w_{i}\in \mathbf {C} ,\forall \mathbf {a} \in \mathbf {A} ,\mathbf {b} \in \mathbf {B} ,\phi (\mathbf {a} ,\mathbf {b} )=\sum _{i=1}^{r}f_{i}(\mathbf {a} )g_{i}(\mathbf {b} )w_{i}\right.\right\}$

Drugim rečima, rang bilinearne mape je dužina njenog najkraćeg bilinearnog računa. Postojanje Štrasenovog algoritma pokazuje da rang množenja 2×2 matrica nije veći od sedam. Da bismo se uverili, koristimo brzi algoritam (uz standardni algoritam) kao takav bilinearni račun. U slučaju matrica, dualni prostori A* i B* se sastoje od mapa u polju F indukovanih skalarnim vektorskim proizvodom, (t.j. u ovom slučaju zbirom svih elemenata Hadamardovog proizvoda.)

	Standardni algoritam				Štrasenov algoritam
i	fi(a)	gi(b)	wi		fi(a)	gi(b)	wi
1	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}$		${\begin{bmatrix}1&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&1\end{bmatrix}}$
2	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}$		${\begin{bmatrix}0&0\\1&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\1&-1\end{bmatrix}}$
3	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}$		${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&1\\0&-1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&1\\0&1\end{bmatrix}}$
4	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}$		${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}-1&0\\1&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\1&0\end{bmatrix}}$
5	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}$		${\begin{bmatrix}1&1\\0&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}-1&1\\0&0\end{bmatrix}}$
6	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}$		${\begin{bmatrix}-1&0\\1&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}1&1\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}$
7	${\begin{bmatrix}0&0\\1&0\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&1\\0&0\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}$		${\begin{bmatrix}0&1\\0&-1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\1&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}1&0\\0&0\end{bmatrix}}$
8	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {a}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}:\mathbf {b}$	${\begin{bmatrix}0&0\\0&1\end{bmatrix}}$
	$\mathbf {a} \mathbf {b} =\sum _{i=1}^{8}f_{i}(\mathbf {a} )g_{i}(\mathbf {b} )w_{i}$				$\mathbf {a} \mathbf {b} =\sum _{i=1}^{7}f_{i}(\mathbf {a} )g_{i}(\mathbf {b} )w_{i}$

Može se pokazati da je ukupan broj osnovnih množenja L potrebnih za množenje matrica asimptotski strogo vezan za rang R, t.j. $L=\Theta (R)$, ili preciznije, pošto su konstante poznate, ${\frac {1}{2}}R\leq L\leq R$. Jedno od korisnih svojstava ranga je submultiplikativnost za tenzorske proizvode, što nam omogućava da pokažemo da množenje 2ⁿ×2ⁿ×2ⁿ matrica može biti postignuto sa ne više od 7ⁿ osnovnih množenja za svako n.

Saveti za implementaciju

Do sad smo pretpostavljali da su matrice kvadratne, i da su dimenzije stepena dvojke, i da se matrice proširuju, ukoliko je potrebno. Ovi uslovi omogućavaju matricama da se polove sve dok se u množenju ne dođe do limita ili skalara. Takođe, te restrikcije nam olakšavaju objašnjenje i analizu složenosti, ali nisu neophodne. Popunjavanje matrice na način koji je ranije opisan, ustvari, povećava vreme izračunavanja, i može smanjiti ili u potpunosti ukinuti vreme koje sačuvano korišćenjem ove metode

Radi dobre implementacije treba primetiti:

• Nije potrebno, a ni poželjno koristiti Štrasenov algoritam sve do skalarnih vrednosti. U odnosu na konvencionalno množenje matrica, ovaj algoritam dodaje još $O(n^{2})$ sabiranja i oduzimanja. Dakle, ispod određene veličine, bolje je koristiti konvencionalno množenje. Na primer, ako su početne matrice dimenzija 1600x1600, nema potrebe dopunjavati ih do 2048x2048, nego je bolje podeliti ih na podmatrice 25x25 i koristiti standardno množenje.
• Štrasenov algoritam takođe može da se primeni na matrice bilo kojih dimenzija. Ako je dimenzija parna onda se matrica deli na način koji je predhodno opisan, a ako je neparna onda se matrica dopunjuje nula redom i kolonom. Ovakvo dopunjavanje se može izvršiti usput i lenjo, a dodatni redovi i kolone se brišu kad se formira rezultat. Na primer, recimo da su matrice dimenzija 199x199. One se mogu podeliti na dva dela: gore-levo, dimenzija 100x100 i dole-desno, 99x99. Kada je potrebno 99 se može dopuniti do 100. Primetimo da se, na primer, proizvod $M_{2}$ koristi samo u donjem delu izlaza. S obzirom da levi činilac $(A_{2,1}+A_{2,2})$ ima samo 99 redova, nema potrebe dodavati 100. red u sumu. Jedino što je potrebno dodaviti je kolona u $A_{2,2}$ da bi moglo da se množi sa $A_{2,1}$.
• Osim toga, nema potrebe da matrice budu kvadratne. Nekvadratne matrice se mogu podeliti koristeći iste metode kao kvadratne, praveći manje nekvadratne matrice. Ako je razlika broja redova i kolona matrica veoma velika, poželjno je napraviti da matrice budu "kvadratnije". To se postiže jednostavnim metodama:
  • Proizvod [2N x N] * [N x 10N] se može izraziti preko 20 zasebnih [N x N] * [N x N] operacija, sortiranih tako da formiraju rezultat;
  • Proizvod [N x 10N] * [10N x N] se može odrediti sa 100 [N x N] * [N x N] operacija, koje se sabiraju da bi se dobio rezultat.

Ove tehnike otežavaju implementaciju algoritma u odnosu na obično dopunjavanje do stepena dvojke i kvadratne matrice. Ipak, jasno je da onom ko implementira Štrasenov algoritam na neki nekonvencionalni način bitnija efikasnost izvršavanja od jednostavnosti implementacije.

Literatura

• Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill. 2001. ISBN 978-0-262-03293-3.. Chapter 28: Section 28.2: Strassen's algorithm for matrix multiplication, pp. 735–741.

Spoljašnje veze

• Weisstein, Eric W. „Strassen's Formulas”. MathWorld.  (takođe sadrži formule za brzu inverziju matrica)
• Tyler J. Earnest, Strassen's Algorithm on the Cell Broadband Engine
• Simple Strassen's algorithms implementation in C