Декартов правоугли координатни систем

Декартов координатни систем се користи у математици за једнозначно дефинисање положаја тачака у простору. Карактеристика овог система је да су његове координатне осе међусобно нормалне.
Декартов правоугли координатни систем је измислио француски математичар и филозоф Рене Декарт, који је, између осталих ствари, покушавао да споји алгебру и Еуклидску геометрију. Овај рад је много утицао на развој аналитичке геометрије, рачуна и картографије.
Идеја о овом систему је развијена 1637. у два Декартова дела. У другом делу свог Метода предавања, Декарт је увео нову идеју одређивања положаја тачке или предмета на површини, користећи две нормалне осе као помагало за мерење. У Геометрији, Декарт је даље објаснио горе споменути концепт.
Историја
[уреди | уреди извор]Заслуга за откриће Картезијевог координатног система припала је француском математичару Рене Декарту (1596—1650) који га је именовао по својој латинској верзији имена Cartesius. Премда је идеја била утемељена још 1637. године одвојено у два записа Декарта и Фермата, потоњи није објавио своје откриће.[1] Француски свештеник Никол Оресм користио је конструкције сличне Декартовим дуго пре времена Декарта и Фермата.[2] Декарт је увео нову замисао одређивања положаја тачке или објекта у равни употребивши две међусобно нормалне осе као мерила.[3] Откриће Картезијевог координатног система значило је велики напредак у математици повезујући најприје Еуклидску геометрију и алгебру. Кружнице, елипсе и друге криве сада су први пут могле бити описиване „картезијским” алгебарским једначинама помоћу координата тачака криве у равни. Развој картезијевог координатног система значајно је допринео даљњем развоју математике и омогућио Њутну и Лајбницу откриће диференцијалног и интегралног рачуна.[4][5]
Премда је Декарт дао координатном систему своје име, треба нагласити да су се слични координатни системи користили и пре њега укључивши Абу Рајхан Мухамед ибн Ахмед Бирунија, те Персијску математику X и XI века. Након Декарта развијени су и други координатни системи као што су поларни, сферични, цилиндрични и други.
Декартов координатни систем
[уреди | уреди извор]Налик земљописној карти где је положај неког места одређен с два податка: земљописном ширином и земљописном дужином, нацртају ли се два међусобно нормална бројевна правца, на пример x и y - уобичајено x хоризонталан, а y вертикалан, који се секу у тачки O и одреде ли се на правцима x и y јединичне тачке E и F, тако да је /OE/=/OF/=1, тиме је дефинисан правоугаони или Картезијев координатни систем у равни.
Декартов координатни систем се може користити у простору (где се користе три координате: x, y и z) и у вишедимензионалним системима.
Декартов координатни систем у равни
[уреди | уреди извор]
Дводимензиони Декартов координатни систем се користи да једнозначно одреди сваку тачку у равни помоћу два броја, који се обично означавају са x и y. Декартов координатни систем је дефинисан са две осе (x-оса или апсциса и y-оса или ордината). Избором мере за сваку осу и означавањем јединица мере дуж оса формира се скала.

Коришћењем Декартовог координатног система геометријске фигуре (као што су криве) се могу исказати алгебарским једначинама, тј. једначинама које задовољавају координате на тачкама које леже на фигури. На пример, круг полупречника 2 се може приказати формулом x2 + y2 = 4.
Тродимензионални Декартов координатни систем
[уреди | уреди извор]
Картезијев координатни систем се може изабрати и као о једнодимензионални математички простор, где ће такав простор бити одређен једном осом уз избор оријентације осе и јединичне дужине, а координата (једна) ће у том случају одређивати положај тачке на бројевном правцу који је придружен координатној оси.

Картезијев дводимензионални координатни систем одређује положај тачке у равни, а картезијев тродимензионални координатни систем одређује положај тачке у простору где је такав координатни систем дефинисан средиштем координатног система 0, и три оијентиране осе (x, y и z) с одговарајућим јединичним дужинама. Координате сваке тачке у таквом систему задате су уређеним скупом од 3 броја, на пример (3, -1, 5) који означавају одговарајуће координате у тродимензионалном математичком простору, где су координате представљене оријентисаним нормалним удаљеностима од неке тачке до одговарајуће равни. У тродимензионалном координатном систему називи оса (апсциса и ордината) нису мандаторне, али ако се употребљавају тада је уобичајено да се трећа, z оса, назвати апликата. На исти начин је уобичајено да се x и y оса поставе у хоризонталну раван, а преостала z оса нормално на њих. Коначно, тродимензионални координатни систем се дили на осам подручја, „октаната”, омеђених са одговарајућим деловима равни. Први октант је онај где су све три полуосе позитивне.
Вишедимензионални Декартов координатни систем
[уреди | уреди извор]Следећи наведени принцип генерално се могу координате тачке одредити и у n-димензионалном математичком простору где ће се помоћу n одговарајућих координата дефинисати оријентисана удаљеност од тачке до једне од n хиперравни. У четвородимензионалном математичком простору на пример, постојаће четири осе x, y, z и w, а координате сваке тачке у таквом математичком простору биће одређене уређеним скупом од четири броја.
Непосредне примене и својства
[уреди | уреди извор]Удаљеност између две тачке у равни
[уреди | уреди извор]Удаљеност две тачке у равни одређена Картезијевим координатама и је
што је вид израза Питагорине теореме исказане у Картезијевом координатном систему.
Средиште дужи
[уреди | уреди извор]Нека је дужина задата тачкама A и B и њиховим координатама A и B, тада ће средиште дужи имати координате
- и
- .
Координате тежишта троугла
[уреди | уреди извор]Нека је троугао ABC смештен у Картезијевом координатном систему и одређен тачкама с координатама A, B и C, тада ће тежиште троугла имати координате
- и
- .
Удаљеност између две тачке у простору
[уреди | уреди извор]Удаљеност две тачке у простору одређене у тродимензионалном Картезијевом координатном систему и је
што се може утврдити применом Питагорине теореме.
Транслација
[уреди | уреди извор]Скуп тачака у равни, на пример троугла ABC, може се помакнути у равни уз очување међусобних удаљености и оријентације уз додавање утврђеног пара бројева (X,Y) Картезијевим координатама сваке тачке скупа. Ако су координате тачака троугла A(x’, y’), B(x’’, y’’) и C(x’’’, y’’’) тада ће транслирани, одн. помакнути троугао имати координате A’(x’+X, y’+Y), B’(x’’+X, y’’+Y) и C’(x’’’+X, y’’’+Y)
Увећање, смањење
[уреди | уреди извор]У Картезијевим координатама неки лик може се учинити већим или мањим тако што се све координате свих тачака помноже фактором пропорционалности, нпр. m. Ако су координате тачака које одређују дужину AB, A(x’, y’) и B(x’’, y’’) тада нове координате тачака које одређују дужину A’B’ ће бити A’(mx’, my’) и B’(mx’’, my’’). Ако је m>1 добијени лик ће бити већи, а ако је m<1 добијени лик ће бите мањи од изворног лика.

Приказ кривих у координатном систему у равни
[уреди | уреди извор]У Картезијевом координатном систему једноставно се приказују криве у равни (кружница, елипса, парабола и тд.) те различите функције (линеарне, полиномне, експоненцијалне, тригонометријске и тд.).
Приказујући на пример кружницу у Картезијевом координатном систему установљава се да за сваку тачку кружнице вреди да је
те ће према томе једначина кружнице полупречника 2 (слика десно) бити
Приказ вектора у Картезијевим координатама
[уреди | уреди извор]Тачка у простору описаном Картезијевим координатама може дефинисати вектор. Вектор помака, на пример r, може имати хватиште у исходишту Декартовог координатног система и врх у тачки у простору. Стрелица која показује према врху вектора дефинише смер вектора (смер помака), а ортогоналне пројекције на оси x, y и z одговарајући помак у x, y или z смеру. Дужина самог вектора тада је апсолутна величина помака у простору
- ,
а такође се може записати да је
- ,
где су i, j и k јединични вектори у смеру x, y и z осе.
Вектор у Картезијевом тродимензионалном простору одређен је на тај начин у целости уређеним скупом од четири величине (r, x, y, z). Овакав приказ вектора увео је Вилијам Роуан Хамилтон.
Примене
[уреди | уреди извор]Свака оса може у практичној примени према потреби да има различите мерне јединице (килограме, секунде, вате, итд), што значи да се Картезијевим координатним системом могу приказивати не само криве, лукови и геометријска тела у дводимензионалном, односно тродимензионалном простору, већ да се могу приказивати и све могуће остале промењиве (маса, време, енергија, сила и многе друге). Премда је тешко визуализовати четворо и вишедимензионалне просторе, алгебра Картезијевих координата може се једноставно проширити на четири или више променљивих тако да се могу извршити прорачуни вредности функција и са четири или више променљивих. Таква алгебра дефинише геометрију вишедимензионих простора.
Значај
[уреди | уреди извор]Картезијеве координате су темељ аналитичке геометрије и осигуравају геометријску интерпретацију за бројна подручја математике као што су линеарна алгебра, комплексна анализа, диференцијална геометрија итд. Један од најпознатијих примера је концепт графичког приказа или графа функције. Картезијске координате су основно оруђе у многим подручјима која се баве геометријом укључујући астрономију, физику, техничке струке, економију и другде.
Оријентација
[уреди | уреди извор]Две димензије
[уреди | уреди извор]
Фиксирање или избор x-осе одређује y-осе све до правца. Наиме, y-оса је нужно окомита на x-осу кроз тачку означену 0 на x-оси. Али постоји избор коју од две полуправе на нормали означити као позитивну, а коју као негативну. Сваки од ова два избора одређује другачију оријентацију картезијанске равни.
Уобичајени начин оријентације равни, при чему је позитивна x-оса усмерена удесно, а позитивна y-оса усмерена нагоре (x-оса је "прва", а y-оса "друга" оса), сматра се да је позитивна или стандардна оријентација, која се назива и деснострана оријентација.
Често коришћена мнемоника за дефинисање позитивне оријентације је правило десне руке. Постављањем донекле затворене десне руке на раван са палцем окренутим нагоре, прсти упиру од x-осе ка y-оси, у позитивно оријентисаном координатном систему. Други начин оријентације равни је праћење правила леве руке, постављање леве руке на раван са палцем окренутим нагоре. Када се палац усмери од почетка дуж осе ка позитивном, закривљеност прстију указује на позитивну ротацију дуж те осе. Без обзира на правило које се користи за оријентацију равни, ротирање координатног система ће сачувати оријентацију. Промена било које осе ће обрнути оријентацију, али мењање обе ће оставити оријентацију непромењеном.
Три димензије
[уреди | уреди извор]

Када су x- и y-осе специфициране, оне одређују линију дуж које треба да лежи z-оса, али постоје две могуће оријентације за ову линију. Два могућа координатна система, која резултирају, називају се 'десноруки' и 'леворуки'.[6] Стандардна оријентација, где је xy раван хоризонтална, а z-оса усмерена нагоре (а x- и y-оса формирају позитивно оријентисан дводимензионални координатни систем у xy-равни ако се посматра одозго xy-равни) назива се десна или позитивна.
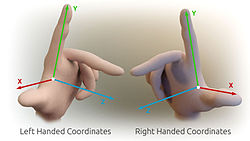
Име потиче од правила десне руке. Ако је кажипрст десне руке усмерен напред, средњи прст савијен према унутра под правим углом у односу на њега, а палац постављен под правим углом према оба, три прста означавају релативну оријентацију x-, y-, и z-осе у десноруком систему. Палац означава x-осу, кажипрст y-осу, а средњи прст z-осу. Насупрот томе, ако се исто уради левом руком, настаје леворуки систем.
Слика 7 приказује леворуки и десноруки координатни систем. Пошто је тродимензионални објекат представљен на дводимензионалном екрану, долази до изобличења и двосмислености. Оса која је усмерена надоле (и удесно) такође треба да показује ка посматрачу, док „средња“ оса треба да показује даље од посматрача. Црвени круг је паралелан са хоризонталном xy-равнином и означава ротацију од x-осе до y-осе (у оба случаја). Дакле, црвена стрелица пролази испред z-осе.
Слика 8 је још један покушај да се прикаже десноруки координатни систем. Опет, постоји нејасноћа узрокована пројектовањем тродимензионалног координатног система у раван. Многи посматрачи виде слику 8 као „превртање“ између конвексне коцке и конкавног „угла“. Ово одговара двема могућим оријентацијама простора. Гледање на фигуру као конвексну даје леворуки координатни систем. Стога је „тачан“ начин да се сагледа слика 8 да се замисли x-оса као да је усмерена ка посматрачу и да се тако види конкавни угао.
Представљање вектора у стандардној бази
[уреди | уреди извор]Тачка у простору у Декартовом координатном систему такође може бити представљена вектором положаја, који се може замислити као стрелица која показује од почетка координатног система до дате тачке.[7] Ако координате представљају просторне позиције (померања), уобичајено је да се вектор од почетка до тачке интересовања представља као . У две димензије, вектор од координатног почетка до тачке са Декартовим координатама (x, y) се може написати као:
где су и јединични вектори у правцу x-осе и y-осе респективно, који се генерално називају стандардном основом (у неким областима примене они се такође могу називати версори). Слично, у три димензије, вектор од координатног почетка до тачке са Декартовим координатама се може написати као:[8]
где је и
Не постоји природна интерпретација вектора множења да би се добио други вектор која функционише у свим димензијама, али постоји начин да се користе комплексни бројеви да се обезбеди такво множење. У дводимензионалној картезијанској равни, идентификује се тачка са координатама (x, y) са комплексним бројем z = x + iy. Овде је i имагинарна јединица и идентификује се са тачком са координатама (0, 1), тако да није јединични вектор у правцу x-осе. Пошто се комплексни бројеви могу помножити дајући други комплексни број, ова идентификација пружа средство за „множење” вектора. У тродимензионалном картезијанском простору слична идентификација се може извршити са подскупом кватерниона.
Референце
[уреди | уреди извор]- ^ Bix, Robert A.; D'Souza, Harry J. „Analytic geometry”. Encyclopædia Britannica. Приступљено 6. 08. 2017.
- ^ Kent, Alexander J.; Vujakovic, Peter (4. 10. 2017). The Routledge Handbook of Mapping and Cartography (на језику: енглески). Routledge. ISBN 9781317568216.
- ^ Burton 2011, p. 374
- ^ A Tour of the Calculus, David Berlinski
- ^ Axler, Sheldon (2015). Linear Algebra Done Right - Springer. Undergraduate Texts in Mathematics. стр. 1. ISBN 978-3-319-11079-0. doi:10.1007/978-3-319-11080-6.
- ^ Anton, Bivens & Davis 2021, стр. 657
- ^ Brannan, Esplen & Gray 1998, Appendix 2, pp. 377–382
- ^ Griffiths 1999
Литература
[уреди | уреди извор]- Brennan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998). Geometry. Cambridge: Cambridge University Press. ISBN 978-0-521-59787-6.
- Smart, James R. (1998). Modern Geometries (5th Ed). Pacific Grove: Brooks/Cole. ISBN 978-0-534-35188-5.
- Descartes, René (2001). Discourse on Method, Optics, Geometry, and Meteorology. Trans. by Paul J. Oscamp (Revised изд.). Indianapolis, IN: Hackett Publishing. ISBN 978-0-87220-567-3. OCLC 488633510.
- Korn, G. A.; Korn, TM (1961). Mathematical Handbook for Scientists and Engineers (1st изд.). New York: McGraw-Hill. стр. 55-79. LCCN 59-14456. OCLC 19959906.
- Margenau, Henry; Murphy, GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. LCCN 55-10911.
- Moon, P.; Spencer, DE (1988). „Rectangular Coordinates (x, y, z)”. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd, 3rd print изд.). New York: Springer-Verlag. стр. 9—11 (Table 1.01). ISBN 978-0-387-18430-2.
- Morse, Philip M. Herman Feshbach (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. ISBN 978-0-07-043316-8. LCCN 52-11515.
- Sauer, R.; Szabó, I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. LCCN 67-25285.
- Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics. Springer. ISBN 978-3-319-11079-0. doi:10.1007/978-3-319-11080-6. Архивирано из оригинала 27. 5. 2022. г. Приступљено 17. 4. 2022.
- Berlinski, David (2011). A Tour of the Calculus. Knopf Doubleday Publishing Group. ISBN 9780307789730.
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998). Geometry. Cambridge: Cambridge University Press. ISBN 978-0-521-59787-6.
- Burton, David M. (2011). The History of Mathematics/An Introduction (7th изд.). New York: McGraw-Hill. ISBN 978-0-07-338315-6.
- Griffiths, David J. (1999). Introduction to Electrodynamics
 . Prentice Hall. ISBN 978-0-13-805326-0.
. Prentice Hall. ISBN 978-0-13-805326-0. - Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013). Calculus: Single and Multivariable (6th изд.). John Wiley & Sons. ISBN 978-0470-88861-2.
- Kent, Alexander J.; Vujakovic, Peter (2017-10-04). The Routledge Handbook of Mapping and Cartography (на језику: енглески). Routledge. ISBN 9781317568216.
- Anton, Howard; Bivens, Irl C.; Davis, Stephen (2021). Calculus: Multivariable. John Wiley & Sons. стр. 657. ISBN 978-1-119-77798-4.
Спољашње везе
[уреди | уреди извор]- Cartesian Coordinate System
- Printable Cartesian Coordinates
- MathWorld description of Cartesian coordinates
- „Cartesian coordinates”. PlanetMath.
- Coordinate Converter – converts between polar, Cartesian and spherical coordinates
- Coordinates of a point Interactive tool to explore coordinates of a point
- open source JavaScript class for 2D/3D Cartesian coordinate system manipulation
























