Дијаграм расејања

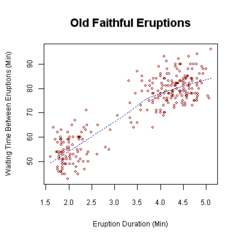
Време чекања између ерупција и трајање ерупције за Стари верни гејзир у Националном парку Јелоустоун, Вајоминг, САД. Овај графикон сугерише да генерално постоје две врсте ерупција: учестане-краткотрајне и споре-дуготрајне.

Дијаграм расејања (која се такође зове тачкасти или граф расејања)^[1] је тип математичког дијаграма који користи картезијанске координате да прикаже вредности за типично две променљиве за неки скуп података. Ако су тачке кодиране (боја/облик/величина), може се приказати једна додатна променљива. Подаци се приказују као колекција тачака, од којих свака има вредност једне променљиве која одређује положај на хоризонталној оси и вредност друге варијабле која одређује положај на вертикалној оси.^[2]

Преглед

Дијаграм расејања може се користити или када је једна континуирана променљива под контролом експериментатора, док друга зависи од ње или када су обе континуиране променљиве независне. Ако постоји параметар који се систематски повећава и/или смањује другим, он се назива контролни параметар или независна променљива и обично се исцртава на хоризонталној оси. Измерена или зависна варијабла се обично приказује дуж вертикалне осе. Ако не постоји зависна променљива, било који тип променљиве се може нацртати на било којој оси, а дијаграм расејања ће илустровати само степен корелације (не узрочне везе) између две променљиве.

Дијаграм расејања може да предложи различите врсте корелација између променљивих са одређеним интервалом поверења. На пример, тежина и висина би били на $y$ -оси, а висина би била на $x$ -оси. Корелације могу бити позитивне (растуће), негативне (опадајуће) или нулте (некорелиране). Ако шаблон тачака од доњег левог ка горњем десном онда то указује на позитивну корелацију између променљивих које се проучавају. Ако се шаблон тачака нагиба од горњег левог ка доњем десном, то указује на негативну корелацију. Линија најбољег уклапања (алтернативно названа 'линија тренда') може се повући за проучавање односа између променљивих. Једначина за корелацију између променљивих може се одредити установљеним процедурама "најбољег уклапања". За линеарну корелацију, најбоља процедура је позната као линеарна регресија и гарантовано ће генерисати тачно решење у коначном времену. Ниједна универзална процедура "најбољег уклапања" није загарантована да генерише исправно решење за произвољне релације. Дијаграм расејања је такође веома користан када желимо да видимо како се два упоредива скупа података слажу да покажу нелинеарне односе између варијабли. Могућност да се ово уради може се побољшати додавањем глатке линије као што је LOESS . Штавише, ако су подаци представљени комбинованим моделом једноставних релација, ове релације ће бити визуелно евидентне као суперпонирани шаблони.

Дијаграм расејања је један од седам основних алата контроле квалитета.^[3]

Графикони расејања могу бити направљени у облику балончића, маркера и/или линијских графикона .

Пример

На пример, да би приказали везу између нечијег капацитета плућа и могућности да особа задржи дах на неки временски период, истраживач би изабрао групу људи за проучавање, а затим измерио капацитет плућа сваке особе (прва променљива) и колико дуго та особа може да задржи дах (друга променљива). Истраживач би затим исцртао податке у дијаграму расејања, додељујући "капацитет плућа" хоризонталној оси, а "време задржавања даха" вертикалној оси.

Особа са капацитетом плућа од 7002400000000000000♠400 cl која је задржала дах 7001217000000000000♠21,7 s би била представљена једном тачком на дијаграму расејања у тачки (400, 21.7) у Декартовим координатама. Дијаграм расејања свих људи у студији би омогућио истраживачу да добије визуелно поређење две променљиве у скупу података и помогао би да се утврди какав би однос могао постојати између те две променљиве.

Матрице дијаграма расејања

За скуп променљивих података (димензија) X ₁, X ₂, . ., X _к, матрица дијаграма расејања показује све дијаграме расејања променљивих у пару на једном приказу са више дијаграма расејања у формату матрице. За $k$ променљивих, матрица дијаграма расејања ће садржати $k$ редова и $k$ колона. Графикон који се налази на пресеку реда $j$ -те колоне је дијаграм променљивих X_i наспрам X_ј. То значи да су сваки ред и колона једна димензија, а свака ћелија приказује дијаграм расејања две димензије.

Генерализована матрица дијаграма расејања нуди низ приказа упарених комбинација категоричких и квантитативних променљивих. Мозаик дијаграм, дијаграм флуктација или обрушени тракасти дијаграм се може користити за приказ две категоричке променљиве. Остали графикони се користе за једну категоријску и једну квантитативну променљиву.

Пример дијаграма распиања

Види још

Референце

^ Jarrell, Stephen B. (1994). Basic Statistics (Special pre-publication изд.). Dubuque, Iowa: Wm. C. Brown Pub. стр. 492. ISBN 978-0-697-21595-6. „When we search for a relationship between two quantitative variables, a standard graph of the available data pairs (X,Y), called a scatter diagram, frequently helps...”
^ Utts, Jessica M. Seeing Through Statistics 3rd Edition, Thomson Brooks/Cole. 2005. ISBN 0-534-39402-7. стр. 166-167.
^ Nancy R. Tague (2004). „Seven Basic Quality Tools”. The Quality Toolbox. Milwaukee, Wisconsin: American Society for Quality. стр. 15. Архивирано из оригинала 31. 10. 2018. г. Приступљено 2010-02-05.

Литература

Jarrell, Stephen B. (1994). Basic Statistics (Special pre-publication изд.). Dubuque, Iowa: Wm. C. Brown Pub. стр. 492. ISBN 978-0-697-21595-6. „When we search for a relationship between two quantitative variables, a standard graph of the available data pairs (X,Y), called a scatter diagram, frequently helps...”

Спољашње везе

Медији везани за чланак Дијаграм расејања на Викимедијиној остави
Шта је дијаграм расејања? Архивирано на сајту Wayback Machine (7. август 2020)
Correlation scatter-plot matrix for ordered-categorical data – Објашњење и R код
Density scatterplot for large datasets (хиљаде милиона тачака)

[1] Jarrell, Stephen B. (1994). Basic Statistics (Special pre-publication изд.). Dubuque, Iowa: Wm. C. Brown Pub. стр. 492. ISBN 978-0-697-21595-6. „When we search for a relationship between two quantitative variables, a standard graph of the available data pairs (X,Y), called a scatter diagram, frequently helps...”

[2] Utts, Jessica M. Seeing Through Statistics 3rd Edition, Thomson Brooks/Cole. 2005. ISBN 0-534-39402-7. стр. 166-167.

[3] Nancy R. Tague (2004). „Seven Basic Quality Tools”. The Quality Toolbox. Milwaukee, Wisconsin: American Society for Quality. стр. 15. Архивирано из оригинала 31. 10. 2018. г. Приступљено 2010-02-05.

[1]

[2]

[3]