Пређи на садржај

Квантно машинско учење

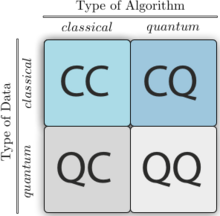
С Википедије, слободне енциклопедије

Квантно машинско учење (енг. Quantum machine learning) јесте нова интердисциплинарна област на пресеку квантне физике и машинског учења.[1][2][3][4] Могу се разликовати четири различита начина спајања две различите родитељске дисциплине.[5][6] Алгоритми квантног машинског учења могу користити предности квантног рачунања како би побољшали класичне методе машинског учења, примера ради, развијањем ефикасних имплементација захтевних класичних алгоритама на квантном рачунару.[7][8][9] Са друге стране, класични методи машинског учења се могу употребити у анализи квантних система. Најопштије, узима се у обзир ситуација у којој су и уређај за учење и систем који се испитује у потпуности квантни.

Повезане гране истраживања истражују методолошке и структурне сличности између одређених физичких система и система учења, посебно неуронских мрежа, што је показало да одређене математичке и нумеричке технике из квантне физике доприносе класичном машинском учењу.[10]

Четири различита приступа за комбиновање дисциплина квантног рачунарства и машинског учења[5][6]Прво слово се односи на то да ли је систем који се проучава класичан или квантни, док друго слово дефинише да ли се користи класични или квантни уређај за обраду података.

Квантно побољшано машинско учење

[уреди | уреди извор]

Квантно побољшање машинског учења односи се на квантне алгоритме[11] који решавају задатке машинског учења, чиме се побољшава класично машинско учење. Овакви алгоритми обично захтевају кодирање класичног скупа података у квантни рачунар, тако да исти постану доступни за квантну обраду информације. Након тога, могу се применити рутине за обраду квантних информација и резултат квантног израчунавања се очитава мерењем квантног система. На пример, исход мерења кубита може открити резултат задатка бинарне класификације.[12] Иако су многи предлози алгоритама за квантно машинско учење и даље чисто теоретски и захтевају тестирање на универзалном квантном рачунару, други су имплементирани на квантним уређајима мале или посебне намене.

Симулације линеарне алгебре квантним амплитудама

[уреди | уреди извор]

Једна врста приступа базирана је на идеји амплитудног кодирања, односно повезивања амплитуде квантног стања са улазима и излазима рачунара.[13][14][15][16] С обзиром да је стање кубита описано са комплексних амплитуда, овакво кодирање информација може омогућити експоненцијално компактно представљање. Интуитивно, ово одговара повезивању дискретне расподеле вероватноће над случајним бинарним променљивим са класичним вектором. Циљ алгоритма заснованог на амплитудном кодирању јесте формулисање квантних алгоритама чији ресурси расту полиномијално са повећањем броја кубита , што даје логаритамски раст броја амплитуда, a тиме и димензије улаза.

Многи алгоритми квантног машинског учења у овој категорији засновани су на варијацијама квантног алгоритма за решавање линеарног система једначина[17] који, под одређеним условима, налази инверз матрице користећи ресурсе који расту логаритамски повећањем димензије матрице. Један од ових специфичних услова јесте да се оператор Хамилтонијан који одговара матрици може ефикасно симулирати, што је могуће ако је матрица проређена[18] или ако је ранг матрице низак[19].

Сваки познати алгоритам за одређивање инверза матрице захтева извршавање броја операција који расте барем квадратно са повећањем димензије матрице.

Квантна метода матричне инверзије може бити примењена у методама машинског учења у којима се тренирање своди на решавање система линеарних једначина, на пример у линеарној регресији методом најмањих квадрата[14][15], или у Гаусовим процесима.[16] Кључни проблем метода које симулирају методе линеарне алгебре израчунавањима користећи амплитуде квантних стања јесте припрема стања, која увек захтева иницијализацију квантног система у стање чије амплитуде верно одражавају карактеристике целог скупа података. Иако су ефикасни методи за припрему стања познати за одређене специфичне проблеме[20][21] овај корак обично скрива сложеност целог задатка.[22]

Алгоритми квантног машинског учења засновани на Гроверовом алгоритму претраге

[уреди | уреди извор]

Још један приступ у циљу побољшања класичног машинског учења користећи квантну обраду информација користи метод појачавања амплитуда заснован на Гроверовом алгоритму претраге, за ког је показано да решава неструктуриране пробелме са квадратним убрзањем у поређењу са класичним алгоритмима. Овакве квантне рутине могу се користити за алгоритме учења који се претварају у неструктуриране алгоримте претраге, што може бити урађено, за на пример, проблем К-медијанске кластеризације[23] и алгоритам к најближих суседа[7]. Још једна примена јесте у квадратном убрзавању машинског учења перцептрона.

Амплитудно појачање се често комбинује са тзв. квантним ходањем како би се постигло квадратно убрзање. Квантно ходање предложено је да побољша Гуглов PageRank Algorithm[24] да му побољша перформансе и учврсти стабилност учења.[25]

Појачано квантно учење

[уреди | уреди извор]

Појачано учење (енг. Reinforcement learning) је трећа грана машинског учења, која се разликује од надгледаног и ненадгледаног машинског учења, у којој су такође могућа квантна побољшања.[26][25][27][28] У квантном побољшању ове гране машинског учења квантни агент интерагује са класичним окружењем и повремено добија награде за своје акције, што му омогућава да прилагоди своје понашање, другим речима, алгоритам учи шта треба да ради да добије што више награда. У неким ситуацијама, било због могућности квантне обраде код агента[25], било због могућности тестирања околине у суперпозицијама[6] може се постићи квантно убрзање. Имплементација ових типова протокола предложене су у неким областима као што су рецимо, суперпроводна кола[29] и сл.

Квантне технике узорковања

[уреди | уреди извор]

Узимање узорака из расподела вероватноће великих димензија јесте у сржи широког спектра рачунарских техника са важним применама у науци, инжењерингу и друштву. Примери укључују такозвано дубоко учење (енг. Deep Learning), пробабилистичко програмирање и разне друге примене машинског учења и вештачке интелигенције. Рачунски тежак проблем, који је кључан за неке релевантне задатке машинског учења, јесте процена просека над пробабилистичким моделима дефинисаним помоћу Болцманове расподеле. Узимање узорака из генеричких пробабилистичких модела је тешко; очекује се да ће алгоритми који се ослањају на ово узорковање остати непоуздани. Иако су квантни анализатори, као они дизајнирани од стране фирме D-Wave Systems, дизајнирани за решавање изазовних комбинаторних оптимизационих проблема, недавно је препознат њихов потенцијал за убрзавање процеса који се ослањају на узорковање коришћењем квантних ефеката.[30] Неке истраживачке групе у новије време су проучавале употребу квантних техника узорковања за учење Болцманових машина и неуронских мрежа.[31][32][33][34] Стандардни приступ за обуку Болцманових машина ослања се на израчунавање одрећених просечних вредности које се могу проценити стандардним техникама узорковања, као што су Markov chain Monte Carlo алгоритам и слични.

Квантне неуронске мреже

[уреди | уреди извор]

Постоје и квантни аналогони, односно генерализација класичних неуронских мрежа[35], које су познате као квантне неуронске мреже.

Теорија квантног учења

[уреди | уреди извор]

Теорија квантног учења почива на математичкој анализи квантних генерализација класичних модела учења и могућих временских и других убрзања ових модела. Принцип је сличан принципу рачунарске теорије учења (енг. Computational learning theory), али је ученик у овом случају квантни уређај за обраду података, док подаци могу бити било класични, било квантни. Квантну теорију учења треба разликовати од напредног машинског учења са квантним побољшањем, код ког је циљ да се размотре специфични проблеми и да се користе квантни протоколи како би се побољшала временска сложеност класичних алгоритама за ове проблеме. Иако се квантна теорија учења још развија, већ су добијени делимични резултати у овој области.[36] Полазна тачка у теорији квантног учења јесте типично појам класе концепата, скупа могућих концепата. Обично, концепт јесте функција дефинисана на неком домену, као што је . На пример, класа концепата може бити скуп формула Дисјунктивне нормалне форме (ДНФ) са битова. Циљ ученика је да научи (тачно или приближно) непознати циљни концепт из ове класе. Ученик може активно интераговати са циљаним концептом или може од истог пасивно примати информације. У активном учењу, ученик може формирати неку врсту упита и исте поставити циљном концепту тражећи вредност за одабране вредности улаза . Ученик тада мора реконструисати тачан циљани концепт са великом вероватноћом. У моделу тачног квантног учења ученик може правити упите у квантној суперпозицији. У случају да се сложеност ученика мери бројем упита које он направи, онда тачни квантни ученици могу бити полиномијално ефикаснији у односу на класичне ученике, али не и више.[37] Ако се сложеност мери количином времена које ученик користи, онда постоје концептуалне класе које могу ефикасно бити научене од стране квантних ученика, али не од стране класичних ученика (при разумним теоријским претпоставкама).[37] Природни модел пасивног учења је Вероватно приближно исправно учење (енг. Probably approximately correct learning, PAC). Овде ученик прима случајне примере , где је вредност распоређена на основу неке (непознате) расподеле . У овом моделу циљ ученика јесте изношење хипотезне функције тако да је са великом вероватноћом када је изабран на основу . Ученик мора бити у стању да изнесе такву приближно тачну хипотезну функцију за сваку расподелу и сваки циљни концепт у својој концептној класи. На овом месту може се размотрити и замена случајних примера са потенцијално моћнијим квантним примерима . У PAC моделу (и сродним моделима) ово неће значајно смањити број потребних примера: за сваку концептуалну класу број потребних класичних и квантних примера разликују се само за константан фактор.[38] Међутим, за учење под неком фиксном расподелом квантни примери могу бити од велике помоћи, на пример за учење ДНФ-а под унифорном расподелом.[39] Ако се разматра временска сложеност, постоји класа концепата која може бити ефикасно научена у PAC моделу користећи квантне ученике, чак и помоћу класичних примера, али не и користећи класичне ученике (опет под разумним теоријским претпоставкама).

Ова пасивна врста учења је такође и најчешћа шема у надгледаном машинском учењу: алгоритам учења обично узима фиксне тренинг примере, без могућности постављања упита на необележене примере. Извођење хипотезе је корак индукције. Класично, индуктивни модел се дели на фазу тренинга и фазу примене: параметри модела се процењују у фази тренинга, па се затим научени модел примењује произвољно много пута у фази примене. У асимптотској граници броја примена, овакво раздвајање фаза је присутно са квантним ресурсима.[40]

Класично учење примењено на квантне системе

[уреди | уреди извор]

Термин квантно машинско учење се такође користи за приступе који примењују класичне методе машинског учења на проучавање квантних система. Основни пример јесте употреба класичних техника учења да се обради велика количина експерименталних података у циљу карактеризације непознатог квантног система (на пример у контексту квантне теорије информација и за развој квантних технологија), али постоје и друге примене истог.

Способност експерименталне контроле и припреме све сложенијих квантних система доноси са собом све већу потребу да се велики скупови података претварају у значајне информације. Ово је проблем који се у великој мери проучавао и у класичном окружењу што за последицу има да многи постојећи алгоритми машинског учења могу бити природно адаптирани у ефикасније формулације. На пример, Бајесовски методи и концепти алгоритамског учења могу бити плодно примењени на проблем класификације квантних стања.

Други проблеми на које се овај приступ може применити:

  • Идентификација тачног модела за динамику квантних система[41][42][43]
  • Извлачење информација о непознатим стањима[44][45][46]
  • Учење непознатих унитарних трансформација

Међутим, карактеризација квантних стања и процеса није једина примена класичних техника машинског учења. Неке додатне примене укључују:

  • Аутоматско генерисање нових квантних експеримената[47]
  • Решавање вишеструке, статичке и временски зависне Шредингерове једначине[48]
  • Генерисање адаптивних шема повратних информација за квантну метрологију[49][50]

Потпуно квантно машинско учење

[уреди | уреди извор]

У општем случају квантног машинског учења, уређај за учење и систем који се испитује, као и њихова интеракција, у потпуности су квантни. Једна класа проблема која може имати профит од пуног квантног приступа јесте учење непознатих квантних стања, процеса и мерења, у смислу да се иста могу репродуковати другом квантном систему. На пример, можда се желе научити мерења која се разликују у два кохерентна стања, када немамо дате класичне описе ових стања која желимо открити, већ уместо тога скуп квантних система у овим стањима. Наиван приступ би био прво да се одреде класични описи стања па затим имплементација идеалног мерења базираног на овим информацијама. То би захтевало једино технике класичног учења. Мећутим, може се показати да је потпуни квантни приступ супериоран у овом случају.[51] (Ово се такође односи и на енг. quantum pattern matching[52]).

Проблему учења унитарних трансформација може се приступити на сличан начин.[53]

Имплементације и експерименти

[уреди | уреди извор]

Најранији експерименти су изведени коришћењем D-Wave квантног рачунара, на пример за откривање аутомобила на дигиталним сликама коришћењем убрзања неконвексном објектном функцијом (извршени 2009.)[54]

D-Wave чип дизајниран да рукује са 128-кубитним квантним процесором

После овога, уследили су многобројни експерименти на истој архитектури и водеће технолошке компаније показале су заинтересованост за потенцијал квантног машинског учења за будуће технолошке имплементације. Године 2013, Гоогле развојни центар, НАСА и Америчка универзитетска свемирска истраживачка асоцијација УСРА онсовали су Квантну лабораторију за машинско учење која истражује употребу и потенцијал адиабатског D-Wave квантног рачунара.[55][56] Користећи другу технологију засновану на нуклеарној магнетној резонанци, квантна Хопфилдова мрежа је имплементирана 2009. године која мапира улазне податке и чува исте и Хамилтонијанима, што допушта могућности адиабатског квантног рачунања.[57]

Недавно је, на основу неуро-миметичког приступа, у поље квантног машинског учења додат нови састојак, у облику тзв. квантног помпорника, квантизованог модела класичног помпорника.[58] Овај уређај се може конструисати помоћу подесивог отпорника, слабих мерења на систему и класичног механизма преноса. Предложена је имплементација квантног помпорника у суперпроводним круговима[59] и изведен је експеримент са квантним тачкама.[60] Квантни помпорник би променио нелинеарне интеракције у квантној динамици која би помогла у потрази за потпуно функционалном квантном неуронском мрежом.

Види још

[уреди | уреди извор]

Референце

[уреди | уреди извор]
  1. ^ Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (2014). „An introduction to quantum machine learning”. Contemporary Physics. 56 (2): 172. Bibcode:2015ConPh..56..172S. arXiv:1409.3097 Слободан приступ. doi:10.1080/00107514.2014.964942. 
  2. ^ Wittek, Peter (2014). Quantum Machine Learning: What Quantum Computing Means to Data Mining. Academic Press. ISBN 978-0-12-800953-6. 
  3. ^ Adcock, Jeremy; Allen, Euan; Day, Matthew; Frick, Stefan; Hinchliff, Janna; Johnson, Mack; Morley-Short, Sam; Pallister, Sam; Price, Alasdair; Stanisic, Stasja (2015). „Advances in quantum machine learning”. arXiv:1512.02900 Слободан приступ [quant-ph]. 
  4. ^ Biamonte, Jacob; Wittek, Peter; Pancotti, Nicola; Rebentrost, Patrick; Wiebe, Nathan; Lloyd, Seth (2016). „Quantum machine learning”. arXiv:1611.09347 Слободан приступ [quant-ph]. 
  5. ^ а б Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (2006). „Machine Learning in a Quantum World”. Advances in Artificial Intelligence (на језику: енглески). Springer, Berlin, Heidelberg: 431—442. doi:10.1007/11766247_37. 
  6. ^ а б в Dunjko, Vedran; Taylor, Jacob M.; Briegel, Hans J. (20. 9. 2016). „Quantum-Enhanced Machine Learning”. Physical Review Letters. 117 (13): 130501. Bibcode:2016PhRvL.117m0501D. arXiv:1610.08251 Слободан приступ. doi:10.1103/PhysRevLett.117.130501. 
  7. ^ а б Wiebe, Nathan; Kapoor, Ashish; Svore, Krysta (2014). „Quantum Algorithms for Nearest-Neighbor Methods for Supervised and Unsupervised Learning”. Quantum Information & Computation ( & 4): (20). 15 (3): 0318—0358. Bibcode:2014arXiv1401.2142W. arXiv:1401.2142 Слободан приступ. 
  8. ^ Lloyd, Seth; Mohseni, Masoud; Rebentrost, Patrick (2013). „Quantum algorithms for supervised and unsupervised machine learning”. arXiv:1307.0411 Слободан приступ [quant-ph]. 
  9. ^ Yoo, Seokwon; Bang, Jeongho; Lee, Changhyoup; Lee, Jinhyoung (2013). „A quantum speedup in machine learning: Finding a N-bit Boolean function for a classification”. New Journal of Physics. 16 (10): 103014. Bibcode:2014NJPh...16j3014Y. arXiv:1303.6055 Слободан приступ. doi:10.1088/1367-2630/16/10/103014. 
  10. ^ Bény, Cédric (14. 1. 2013). „Deep learning and the renormalization group”. arXiv:1301.3124 Слободан приступ [quant-ph]. 
  11. ^ У квантном рачунарству квантн алгоритам је алгоритам који је дизајниран за и који се извршава на квантној архитектури
  12. ^ Задатак бинарне класификације своди се на класификовање елемената неког скупа у две групе на основу базног правила класификације
  13. ^ Rebentrost, Patrick; Mohseni, Masoud; Lloyd, Seth (2014). „Quantum Support Vector Machine for Big Data Classification”. Physical Review Letters. 113 (13): 130503. Bibcode:2014PhRvL.113m0503R. PMID 25302877. arXiv:1307.0471 Слободан приступ. doi:10.1103/PhysRevLett.113.130503. 
  14. ^ а б Wiebe, Nathan; Braun, Daniel; Lloyd, Seth (2012). „Quantum Algorithm for Data Fitting”. Physical Review Letters. 109 (5): 050505. Bibcode:2012PhRvL.109e0505W. PMID 23006156. arXiv:1204.5242 Слободан приступ. doi:10.1103/PhysRevLett.109.050505. 
  15. ^ а б Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (2016). „Prediction by linear regression on a quantum computer”. Physical Review A. 94 (2): 022342. Bibcode:2016PhRvA..94b2342S. arXiv:1601.07823 Слободан приступ. doi:10.1103/PhysRevA.94.022342. 
  16. ^ а б Zhao, Zhikuan; Fitzsimons, Jack K.; Fitzsimons, Joseph F. (2015). „Quantum assisted Gaussian process regression”. arXiv:1512.03929 Слободан приступ [quant-ph]. 
  17. ^ Harrow, Aram W.; Hassidim, Avinatan; Lloyd, Seth (2008). „Quantum algorithm for solving linear systems of equations”. Physical Review Letters. 103 (15): 150502. Bibcode:2009PhRvL.103o0502H. PMID 19905613. arXiv:0811.3171 Слободан приступ. doi:10.1103/PhysRevLett.103.150502. 
  18. ^ Berry, Dominic W.; Childs, Andrew M.; Kothari, Robin (2015). Hamiltonian simulation with nearly optimal dependence on all parameters. 56th Annual Symposium on Foundations of Computer Science. IEEE. стр. 792—809. arXiv:1501.01715 Слободан приступ. doi:10.1109/FOCS.2015.54. 
  19. ^ Lloyd, Seth; Mohseni, Masoud; Rebentrost, Patrick (2014). „Quantum principal component analysis”. Nature Physics. 10 (9): 631. Bibcode:2014NatPh..10..631L. arXiv:1307.0401 Слободан приступ. doi:10.1038/nphys3029. 
  20. ^ Soklakov, Andrei N.; Schack, Rüdiger (2006). „Efficient state preparation for a register of quantum bits”. Physical Review A. 73: 012307. Bibcode:2006PhRvA..73a2307S. doi:10.1103/PhysRevA.73.012307. 
  21. ^ Giovannetti, Vittorio; Lloyd, Seth; MacCone, Lorenzo (2008). „Quantum Random Access Memory”. Physical Review Letters. 100 (16): 160501. Bibcode:2008PhRvL.100p0501G. PMID 18518173. arXiv:0708.1879 Слободан приступ. doi:10.1103/PhysRevLett.100.160501. 
  22. ^ Aaronson, Scott (2015). „Read the fine print”. Nature Physics. 11 (4): 291. Bibcode:2015NatPh..11..291A. doi:10.1038/nphys3272. 
  23. ^ Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (1. 2. 2013). „Quantum speed-up for unsupervised learning”. Machine Learning (на језику: енглески). 90 (2): 261—287. ISSN 0885-6125. doi:10.1007/s10994-012-5316-5. 
  24. ^ Paparo, Giuseppe Davide; Martin-Delgado, Miguel Angel (2012). „Google in a Quantum Network”. Scientific Reports. 2: 444. Bibcode:2012NatSR...2E.444P. PMC 3370332 Слободан приступ. PMID 22685626. arXiv:1112.2079 Слободан приступ. doi:10.1038/srep00444. 
  25. ^ а б в Paparo, Giuseppe Davide; Dunjko, Vedran; Makmal, Adi; Martin-Delgado, Miguel Angel; Briegel, Hans J. (2014). „Quantum Speedup for Active Learning Agents”. Physical Review X. 4 (3): 031002. Bibcode:2014PhRvX...4c1002P. arXiv:1401.4997 Слободан приступ. doi:10.1103/PhysRevX.4.031002. 
  26. ^ Dong, Daoyi; Chen, Chunlin; Li, Hanxiong; Tarn, Tzyh-Jong (2008). „Quantum Reinforcement Learning”. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics). 38 (5): 1207. doi:10.1109/TSMCB.2008.925743. 
  27. ^ Crawford, Daniel; Levit, Anna; Ghadermarzy, Navid; Oberoi, Jaspreet S.; Ronagh, Pooya (2016). „Reinforcement Learning Using Quantum Boltzmann Machines”. arXiv:1612.05695 Слободан приступ [quant-ph]. 
  28. ^ Briegel, Hans J.; Cuevas, Gemma De las (15. 5. 2012). „Projective simulation for artificial intelligence”. Scientific Reports (на језику: енглески). 2. Bibcode:2012NatSR...2E.400B. ISSN 2045-2322. PMC 3351754 Слободан приступ. PMID 22590690. arXiv:1104.3787 Слободан приступ. doi:10.1038/srep00400. 
  29. ^ Lamata, Lucas (2017). „Basic protocols in quantum reinforcement learning with superconducting circuits”. Scientific Reports. 7: 1609. Bibcode:2017NatSR...7.1609L. arXiv:1701.05131 Слободан приступ. doi:10.1038/s41598-017-01711-6. 
  30. ^ Biswas, Rupak; Jiang, Zhang; Kechezi, Kostya; Knysh, Sergey; Mandrà, Salvatore; O’Gorman, Bryan; Perdomo-Ortiz, Alejando; Pethukov, Andre; Realpe-Gómez, John; Rieffel, Eleanor; Venturelli, Davide; Vasko, Fedir; Wang, Zhihui (2016). „A NASA perspective on quantum computing: Opportunities and challenges”. Parallel Computing. doi:10.1016/j.parco.2016.11.002. 
  31. ^ Adachi, Steven H.; Henderson, Maxwell P. (2015). „Application of quantum annealing to training of deep neural networks”. arXiv:1510.06356 Слободан приступ [quant-ph]. 
  32. ^ Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (2016). „Quantum-assisted learning of graphical models with arbitrary pairwise connectivity”. arXiv:1609.02542 Слободан приступ [quant-ph]. 
  33. ^ Benedetti, Marcello; Realpe-Gómez, John; Biswas, Rupak; Perdomo-Ortiz, Alejandro (2016). „Estimation of effective temperatures in quantum annealers for sampling applications: A case study with possible applications in deep learning”. Physical Review A. 94 (2): 022308. Bibcode:2016PhRvA..94b2308B. arXiv:1510.07611 Слободан приступ. doi:10.1103/PhysRevA.94.022308. 
  34. ^ Korenkevych, Dmytro; Xue, Yanbo; Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Rolfe, Jason; Andriyash, Evgeny (2016). „Benchmarking quantum hardware for training of fully visible Boltzmann machines”. arXiv:1611.04528 Слободан приступ [quant-ph]. 
  35. ^ Wan, Kwok-Ho; Dahlsten, Oscar; Kristjansson, Hler; Gardner, Robert; Kim, Myungshik (2016). „Quantum generalisation of feedforward neural networks”. Bibcode:2016arXiv161201045W. arXiv:1612.01045 Слободан приступ. 
  36. ^ Arunachalam, Srinivasan; de Wolf, Ronald (2017). „A Survey of Quantum Learning Theory”. arXiv:1701.06806 Слободан приступ [quant-ph]. 
  37. ^ а б Servedio, Rocco A.; Gortler, Steven J. (2004). „Equivalences and Separations Between Quantum and Classical Learnability”. SIAM Journal on Computing. 33 (5): 1067—1092. doi:10.1137/S0097539704412910. 
  38. ^ Arunachalam, Srinivasan; de Wolf, Ronald (2016). „Optimal Quantum Sample Complexity of Learning Algorithms”. arXiv:1607.00932 Слободан приступ [quant-ph]. 
  39. ^ Nader, Bshouty H.; Jeffrey, Jackson C. (1999). „Learning DNF over the Uniform Distribution Using a Quantum Example Oracle”. SIAM Journal on Computing. 28 (3): 1136—1153. doi:10.1137/S0097539795293123. 
  40. ^ Monràs, Alex; Sentís, Gael; Wittek, Peter (2017). „Inductive supervised quantum learning”. Physical Review Letters. 118 (19): 190503. Bibcode:2017PhRvL.118s0503M. arXiv:1605.07541 Слободан приступ. doi:10.1103/PhysRevLett.118.190503. 
  41. ^ Granade, Christopher E.; Ferrie, Christopher; Wiebe, Nathan; Cory, D. G. (3. 10. 2012). „Robust Online Hamiltonian Learning”. New Journal of Physics. 14 (10): 103013. Bibcode:2012NJPh...14j3013G. ISSN 1367-2630. arXiv:1207.1655 Слободан приступ. doi:10.1088/1367-2630/14/10/103013. 
  42. ^ Wiebe, Nathan; Granade, Christopher; Ferrie, Christopher; Cory, D. G. (14. 5. 2014). „Hamiltonian Learning and Certification Using Quantum Resources”. Physical Review Letters. 112 (19): 190501. Bibcode:2014PhRvL.112s0501W. ISSN 0031-9007. PMID 24877920. arXiv:1309.0876 Слободан приступ. doi:10.1103/PhysRevLett.112.190501. 
  43. ^ Wiebe, Nathan; Granade, Christopher; Ferrie, Christopher; Cory, David G. (17. 4. 2014). „Quantum Hamiltonian Learning Using Imperfect Quantum Resources”. Physical Review A. 89 (4): 042314. Bibcode:2014PhRvA..89d2314W. ISSN 1050-2947. arXiv:1311.5269 Слободан приступ. doi:10.1103/PhysRevA.89.042314. 
  44. ^ Sasaki, Madahide; Carlini, Alberto; Jozsa, Richard (2001). „Quantum Template Matching”. Physical Review A. 64 (2): 022317. Bibcode:2001PhRvA..64b2317S. arXiv:quant-ph/0102020 Слободан приступ. doi:10.1103/PhysRevA.64.022317. 
  45. ^ Sasaki, Masahide (2002). „Quantum learning and universal quantum matching machine”. Physical Review A. 66 (2): 022303. Bibcode:2002PhRvA..66b2303S. arXiv:quant-ph/0202173 Слободан приступ. doi:10.1103/PhysRevA.66.022303. 
  46. ^ Sentís, Gael; Guţă, Mădălin; Adesso, Gerardo (9. 7. 2015). „Quantum learning of coherent states”. EPJ Quantum Technology (на језику: енглески). 2 (1): 17. ISSN 2196-0763. doi:10.1140/epjqt/s40507-015-0030-4. 
  47. ^ Krenn, Mario (1. 1. 2016). „Automated Search for new Quantum Experiments”. Physical Review Letters. 116 (9): 090405. Bibcode:2016PhRvL.116i0405K. PMID 26991161. arXiv:1509.02749 Слободан приступ. doi:10.1103/PhysRevLett.116.090405. 
  48. ^ Carleo, Giuseppe; Troyer, Matthias (9. 2. 2017). „Solving the quantum many-body problem with artificial neural networks”. Science. 355 (6325): 602. Bibcode:2017Sci...355..602C. arXiv:1606.02318 Слободан приступ. doi:10.1126/science.aag2302. 
  49. ^ Hentschel, Alexander (1. 1. 2010). „Machine Learning for Precise Quantum Measurement”. Physical Review Letters. 104 (6). Bibcode:2010PhRvL.104f3603H. arXiv:0910.0762 Слободан приступ. doi:10.1103/PhysRevLett.104.063603. 
  50. ^ Palittpongarnpim, Pantita; Wittek, Peter; Sanders, Barry C. (13. 9. 2016). „Single-shot adaptive measurement for quantum-enhanced metrology”. Quantum Communications and Quantum Imaging XIV. International Society for Optics and Photonics: 99800H—99800H—11. doi:10.1117/12.2237355. 
  51. ^ Sentís, Gael; Guţă, Mădălin; Adesso, Gerardo (9. 7. 2015). „Quantum learning of coherent states”. EPJ Quantum Technology. 2 (1). doi:10.1140/epjqt/s40507-015-0030-4. 
  52. ^ Sasaki, Masahide; Carlini, Alberto (6. 8. 2002). „Quantum learning and universal quantum matching machine”. Physical Review A. 66 (2). Bibcode:2002PhRvA..66b2303S. arXiv:quant-ph/0202173 Слободан приступ. doi:10.1103/PhysRevA.66.022303. 
  53. ^ Bisio, Alessandro; Chiribella, Giulio; D’Ariano, Giacomo Mauro; Facchini, Stefano; Perinotti, Paolo (25. 3. 2010). „Optimal quantum learning of a unitary transformation”. Physical Review A. 81 (3). Bibcode:2010PhRvA..81c2324B. arXiv:0903.0543 Слободан приступ. doi:10.1103/PhysRevA.81.032324. 
  54. ^ „NIPS 2009 Demonstration: Binary Classification using Hardware Implementation of Quantum Annealing” (PDF). Static.googleusercontent.com. Приступљено 26. 11. 2014. 
  55. ^ „Google Quantum A.I. Lab Team”. Google Plus. Google. 31. 1. 2017. Приступљено 31. 1. 2017. 
  56. ^ „NASA Quantum Artificial Intelligence Laboratory”. NASA. NASA. 31. 1. 2017. Архивирано из оригинала 01. 02. 2017. г. Приступљено 31. 1. 2017. 
  57. ^ Neigovzen, Rodion; Neves, Jorge L.; Sollacher, Rudolf; Glaser, Steffen J. (2009). „Quantum pattern recognition with liquid-state nuclear magnetic resonance”. Physical Review A. 79 (4): 042321. Bibcode:2009PhRvA..79d2321N. arXiv:0802.1592 Слободан приступ. doi:10.1103/PhysRevA.79.042321. 
  58. ^ Pfeiffer, P.; Egusquiza, I. L.; Di Ventra, M.; Sanz, M.; Solano, E. (2016). „Quantum memristors”. Scientific Reports. 6: 29507. Bibcode:2016NatSR...629507P. PMC 4933948 Слободан приступ. PMID 27381511. arXiv:1511.02192 Слободан приступ. doi:10.1038/srep29507. 
  59. ^ Salmilehto, J.; Deppe, F.; Di Ventra, M.; Sanz, M.; Solano, E. (2017). „Quantum Memristors with Superconducting Circuits”. Scientific Reports. 7: 42044. Bibcode:2017NatSR...742044S. arXiv:1603.04487 Слободан приступ. doi:10.1038/srep42044. 
  60. ^ Li, Ying; Holloway, Gregory W.; Benjamin, Simon C.; Briggs, G. Andrew D.; Baugh, Jonathan; Mol, Jan A. (2016). „A simple and robust quantum memristor”. arXiv:1612.08409 Слободан приступ [cond-mat.mes-hall]. 


Преузето из „https://sr.wikipedia.org/w/index.php?title=Квантно_машинско_учење&oldid=27762878”