Претрага са нехронолошким враћањем

Претрага са нехронолошким враћањем (енгл. Backjumping) је техника која повећава ефикасност бектрекинг алгоритама. Бектрекинг увек иде један ниво унатраг у стаблу претраге када су тестиране све вредности за променљиву, док се претрагом са нехронолошким враћањем може ићи више нивоа унатраг. У овом чланку се користи статички поредак променљивих $x_{1},\ldots ,x_{n}$, али се иста правила односе и на динамички.

• 
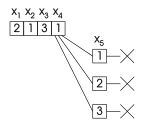
  Стабло претраге посећено регуларним бектрекингом
• 
  Скок унатраг: сиви чвор није посећен

Дефиниција

Кад год су бектрекингом испробане све вредности за променљиву без проналаска решења, преиспитује се последња од раније додељених променљивих, мења јој се вредност или се наставља бектрекинг ако нема других вредности за доделу. Ако је $x_{1}=a_{1},\ldots ,x_{k}=a_{k}$ тренутна делимична додела и све вредности за $x_{k+1}$ су испробане без проналаска решења, закључује се да решење са $x_{1}=a_{1},\ldots ,x_{k}=a_{k}$ не постоји. Алгоритам потом "иде горе" на $x_{k}$ и мења јој вредност ако је могуће, у супротном поново врши бектрекинг.

Није увек неопходна цела делимична додела да би се доказало да ниједна вредност $x_{k+1}$ не води до решења. Префикс делимичне доделе може имати исте особине, то јест, постоји индекс $j<k$ тако да $x_{1},\ldots ,x_{j}=a_{1},\ldots ,a_{j}$ ни са једном вредношћу $x_{k+1}$ не води до решења. Ако алгоритам то може доказати, онда ће одмах разматрати друге вредности за $x_{j}$ уместо разматрања $x_{k}$.

Пример у коме додавање на $x_{1}x_{2}x_{3}x_{4}$ није било успешно ни са једном могућом вредношћу за $x_{5}$. Бектрекинг се враћа на $x_{4}$, и покушава да јој промени вредност.	Уместо бектрекинга, алгоритам врши даљу разраду, доказујући да $x_{1}x_{2}x_{5}=211$, $x_{1}x_{5}=22$, и $x_{1}x_{2}x_{5}=213$ нису делови ниједног решења.	Као резултат, тренутна евалуација $x_{1}x_{2}$ није део ниједног решења, па алгоритам може директно да се врати на $x_{2}$ и покуша да јој додели другу вредност.

Ефикасност алгоритма претраге са нехронолошким враћањем зависи од тога колико далеко се може враћати. У идеалном случају, алгоритам би могао да се врати из $x_{k+1}$ до било које променљиве $x_{j}$ такве да $x_{1},\ldots ,x_{j}$ не формира решење ни са једном вредношћу $x_{k+1}$. Ако је то случај, $j$ се зове сигуран скок.

Није увек могуће утврдити да ли је скок сигуран, јер су сигурни скокови дефинисани у смислу скупа решења, а то је оно што алгоритам покушава да пронађе. У пракси, алгоритми претраге са нехронолошким враћањем користе најнижи индекс за који могу ефикасно доказати да је сигуран скок. Различити алгоритми користе различите методе за утврђивање да ли је скок сигран. Они имају различите трошкове, али се велика цена проналажења већег сигурног скока може смањити редукованом претрагом услед прескакања делова стабла претраге.

Претрага са нехронолошким враћањем на листовима

Најједноставније стање у коме је могућа претрага са нехронолошким враћањем је када је за све вредности променљиве доказано да су неконзистентне без даљег гранања. Делимична евалуација је конзистентна ако и само ако задовољава сва ограничења додељених променљивих, а у супротном је неконзистентна. То може бити случај када се конзистентно делимично решење не може проширити до конзистентног комплетног решења јер неке од недодељених променљивих не могу бити додељене без нарушавања других ограничења.

Стање у коме су све вредности дате променљиве $x_{k+1}$ неконзистентне са тренутним делимичним решењем $x_{1},\ldots ,x_{k}=a_{1},\ldots ,a_{k}$ се зове лист ћорсокак. То се дешава управо када је променљива $x_{k+1}$ лист стабла претраге.

Gaschnig-ов алгоритам претраге са нехронолошким враћањем врши скок унатраг само у листу ћорсокаку. Другим речима, ради другачије од бектрекинга само када су све могуће вредности $x_{k+1}$ тестиране и неконзистентне без потребе за гранањем у другу променљиву.

Сигуран скок се може наћи једноставно, за сваку вредност $a_{k+1}$, тражи се најкраћи префикс од $x_{1},\ldots ,x_{k}=a_{1},\ldots ,a_{k}$ неконзистентан са $x_{k+1}=a_{k+1}$. Другим речима, ако је $a_{k+1}$ могућа вредност за $x_{k+1}$, алгоритам проверава конзистентност следећих евалуација:

$x_{1}=a_{1}$	...	$x_{k-1}=a_{k-1}$	$x_{k}=a_{k}$	$x_{k+1}=a_{k+1}$
$x_{1}=a_{1}$	...	$x_{k-1}=a_{k-1}$		$x_{k+1}=a_{k+1}$
...
$x_{1}=a_{1}$				$x_{k+1}=a_{k+1}$

Најмањи индекс (најнижи унос) за који су евалуације неконзистентне би био сигуран скок да су $x_{k+1}=a_{k+1}$ једине могуће вредности за $x_{k+1}$. Пошто свака променљива обично може имати више од једне вредности, максималан индекс који је добијен провером за сваку вредност је сигуран скок, и то је тачка у коју скаче Gaschnig-ов алгоритам.

У пракси, алгоритам може да испита евалуације изнад док проверава конзистентност $x_{k+1}=a_{k+1}$.

Претрага са нехронолошким враћањем на унутрашњим чворовима

Претходни алгоритам врши нехронолошко враћање само када се вредности променљиве могу показати неконзистентне са тренутним делимичним решењем без даљег гранања. Другим речима, дозвољава се нехронолошко враћање само на листовима у стаблу претраге.

Унутрашњи чвор стабла претраге представља додељену променљиву која је конзистентна са претходним. Ако та додела не даје ниједно решење, претходни алгоритам увек врши бектрекинг: ниједно нехронолошко враћање неће бити извршено у том случају.

Претрага са нехронолошким враћањем на унутрашњим чворовима не може да се изврши као на листовима. Заиста, ако неке евалуације од $x_{k+1}$ захтевају гранање, то је зато што су конзистентне са тренутном доделом. Као резултат, потрага за префиксом који је неконзистентан са овим вредностима последње променљиве није успешна.

У таквим случајевима, оно што доказује да $x_{k+1}=a_{k+1}$ неће бити део решења са тренутном делимичном евалуацијом $x_{1},\ldots ,x_{k}$ је рекурзивна претрага. Посебно, алгоритам "зна" да ниједно решење не постоји од тог тренутка зато што се враћа у тај чвор уместо да се заустави након што је пронашао решење.

Овај повратак је изазван великим бројем ћорсокака, и указује где је алгоритам доказао да је делимично решење неконзистентно. Да би наставио нехроночошко враћање, алгоритам мора имати у виду да решења није могуће наћи због тих ћорсокака. Посебно, сигурни скокови су индекси префикса који и даље чине ћорсокаке неконзистентним делимичним решењима.

У овом примеру, алгоритам се враћа на $x_{k+1}$, након испробавања свих могућих вредности, због три crossed неконзистентне тачке.	Друга тачка остаје неконзистентна чак и када су вредности $x_{k+1}$ и $x_{k}$ уклоњене из делимичне евалуације (уочити да су вредности променљиве у деци)	Друге неконзистентне евалуације остају чак и без $x_{k-2}$, $x_{k-1}$, и $x_{k}$	Алгоритам може да се врати на $x_{k-2}$ јер је то најмања променљива која одржава све неконзистентности. Нова вредност за $x_{k-2}$ ће бити испробана.

Другим речима, када су све вредности $x_{k+1}$ испробане, алгоритам може да се врати на $x_{i}$ под условом да је тренутна истинита евалуација од $x_{1},\ldots ,x_{i}$ неконзистентна са свим истинитим евалуацијама од $x_{k+1},x_{k+2},...$ у листовима који су потомци чвора $x_{k+1}$.

Поједностављења

Док тражимо могући нехронолошки скок за $x_{k+1}$ или једног од његових предака, сви чворови у осенченом подручју могу бити занемарени.

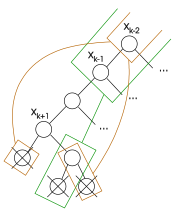
Због потенцијално великог броја чворова који су у подстаблу од $x_{k+1}$, информација која је неопходна да би се безбедно нехронолошки вратило од $x_{k+1}$, се прикупља за време проласка кроз његово подстабло. Проналажење сигурног скока може бити поједностављено помоћу два разматрања. Прво је да је алгоритму потребан сигуран скок, али и даље може да ради са скоком који није највиши могући сигуран скок.

Друго је то да чворови у подстаблу $x_{l}$, који су били прескочени нехронолошким враћањем, могу бити занемарени за време тражења нехронолошког враћања за $x_{l}$. Прецизније, сви чворови прескочени нехронолошким враћањем од чвора $x_{m}$ до чвора $x_{l}$ могу бити заменарени у односу на подстабло чији је корен у $x_{m}$, као и њихова остала подстабла.

Заиста, ако се алгоритам спусти од чвора $x_{l}$ до $x_{m}$ али се нехронолошки врати до самог почетка, онда би уместо тога могао да прође директно од $x_{l}$ до $x_{m}$. Заиста, нехронолошко враћање указује на то да су чворови између $x_{l}$ и $x_{m}$ стварно од мање важности подстаблу чији је корен у $x_{m}$. Другим речима, нехронолошко враћање указује на то да је посећивање области стабла претраге била грешка. Овај део стабла претраге може бити занемарен узимајући у обзир могуће нехронолошко враћање од $x_{l}$ или једног од његових предака.

Променљиве чије су вредности довољне да докажу неправилност у подстаблу чији се корен налази у чвору бивају покупљене у чвору и послате, при повлачењу, (након брисања променљивих у чвору) чвору изнад.

Ова чињеница може бити искоришћена прикуљањем, у сваком чвору, скупа од претходно додељених променљивих чија евалуација не може да докаже да не постоји решење у подстаблу чији је корен у чвору. Овај скуп се прави за време рада алгоритма. При повлачењу из чвора, овај скуп се брише заједно са променљивом чвора и прикупља се у скупу одредишта бектрекинга или нехронолошког враћања. Пошто се чворови који су прескочени нехронолошким враћањем не могу повући, њихови скупови се аутоматски игноришу.

Графовски засновано нехронолошко враћање

Образложење графовски заснованог нехронолошког враћања је у томе да сигуран скок може бити пронађен провером да ли су променљиве $x_{1},\ldots ,x_{k}$ конзистентне са променљивама $x_{k+1},x_{k+2},...$ које су инстанциране у листовима. За сваки леви лист и сваку променљиву $x_{i}$ за индекс $i>k$ који је инстанциран, индекси мањи или једнаки $k$ чија је променљива конзистентна са $x_{i}$, могу бити коришћени за проналажење сигурног скока. Нарочито, када су све вредности за $x_{k+1}$ испробане, овај скуп садржи индексе свих променљивих чије евалуације успевају да докажу да не постоји решење које може бити пронађено посећивањем подстабла чији је корен у $x_{k+1}$. Као резултат, алгоритам се може нехронолошки вратити у највећи индекс у скупу.

Чињеница је да чворови прескочени нехронолошким враћањем могу бити занемарени узимајући у обзир да даље нехронолошко враћање може бити експлоатисано наведеним алгоритмом. При повлачењу из листа, скуп променљивих које ограничене са њим бива креиран и "послат назад" до његовог родитеља, или претка у случају нехронолошког враћања. Скуп променљивих се одржава на сваком унутрашњем чвору. Сваки пут када се скуп променљивих добије од детета или потомка, њихове вредности се додају у одржавани скуп. При даљем бектрекингу или нехронолошком враћању од чвора, променљива чвора се уклања из скупа, и скуп се шаље до чвора одредишта бектрекинга или нехронолошког враћања. Овај алгоритам ради јер одржавани скуп у чвору скупља све променљиве битне за доказивање неправилности у листовама који су потомци чвора. Пошто се скупови променљивих шаљу само за време повлачења из чворова, скупови сакупљени на чворовима прескоченим нехронолошким враћањем бивају занемарени.

Нехронолошко враћање засновано на сукобима

Прерађени алгоритам са нехронолошким враћањем, који може да постигне веће нехронолошко враћање, је базиран не само на проверавању присуства две променљиве у истом ограничењу већ и на проверавању да ли је ограничење изазвало неконзистентност. Нарочито, овај алгоритам прикупља једно од нарушених ограничења у сваком листу. У сваком чвору највећи индекс променљиве који је у једном од ограничења, прикупљен на листовима, представља сигуран скок.

Нарушено ограничење одабрано у сваком листу не утиче на безбедност резултујућег скока. Бирање ограничења највећег могућег индекса повећава висину скока. Из овог разлога, нехронолошко враћање засновано на сукобу нумерише ограничења на такав начин да су мањи индекси већег приоритета у односу на ограничења већих индекса.

Формално, ограничење $C$ је већег приоритета у односу на $D$ ако су највећи индекси променљиве у $C$ мањи у односу на највеће индексе променљиве у $D$. Другим речима, изузимајући заједничке променљиве, ограничење које има све мање индексе има већи приоритет.

На листу, алгоритам бира најмањи индекс $i$ тако да су $x_{1},\ldots ,x_{i}$ неконзистентни са последњном евалуираном променљивом на листу.

Међу ограничењима која су нарушена у евалуацији, алгоритам бира оно са највећим приоритетом, и прикупља све његове индексе мање од $k+1$. На овај начин, када се алгоритам врати до променљиве $x_{k+1}$, најмањи прикупљени индекс представља сигуран скок.

У пракси, алгоритам је поједностављен тако што прикупља све индексе у једнан скуп, уместо креирања скупа за сваку вредност $k$. Нарочито, алгоритам прикупља, у сваком чвору, све скупове који долазе од њихових потомака који нису били прескочени нехронолошким враћањем. При повлачењу из овог чвора, скуп заједно са променљивом се брише из чвора и прикупља се у одредишту бектрекинга или нехронолшког враћања.

Литература

• Dechter, Rina (2003). Constraint Processing. Morgan Kaufmann. ISBN 978-1-55860-890-0. 
• Prosser, Patrick (1993). Hybrid Algorithms for the Constraint Satisfaction Problem (PDF). Computational Intelligence 9(3). Архивирано из оригинала (PDF) 06. 02. 2012. г. Приступљено 12. 05. 2016.