Принцип укључења и искључења

Унија скупова А и Б

У комбинаторици (комбинаторна математика), принцип укључења и искључења је техника бројања која генерализује познати метод добијања броја елемената у унији два коначна скупа; симболично изражена као

$|A\cup B|=|A|+|B|-|A\cap B|,$

где су А и В два коначна комплета скупа и |S| указује на кардиналност скупа S (који се може сматрати као број елемената скупа, ако је скуп коначан). Формула изражава чињеницу да  збир величине два скупа може бити превелики, јер неки елементи могу да се два пута броје. Двоструко-рачунати елементи су они на пресеку два скупа, а датотека се коригује одузимањем величине пресека.

Принцип се јасније види у случају три скупа, који за скупове А, B и C је дат

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|.$

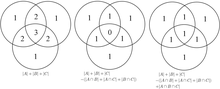
Ова формула се може потврдити бројањем, колико пута сваки регион у Венов дијаграм на слици је укључен у десну страну формуле. У овом случају, када се уклоне доприноси над-пребројаних елемената, број елемената у међусобном пресеку три скупа се одузима сувише често, тако да мора да се дода назад да се добије тачна сума.

Принцип укључења и искључења приказан Веновим дијаграмом са три скупа

Генерализација резултата ових примера даје принцип укључивања и искључивања. Да бисте пронашли кардиналност уједињења n сетова:

1. Укључити кардиналности тих скупова.
2. Искључује кардиналности тих парова пресека.
3. Укључити кардиналности троструко-мудрих пресека. 
4. Искључује кардиналности четвороструко-мудрих пресека.
5. Укључити кардиналности петостуко-мудрих пресека. 
6. Наставите, док кардиналност на n-торка-мудром пресеку је укључена (ако је n непаран) или искључена (чак и n).

Назив потиче од идеје да се принцип заснива на преко-великодушном укључивању, а затим и на компензацији искључивања. Овај концепт се приписује Абрахаму де Моавру (1718); али се први пут појављује у новинама Даниела да Силве (1854), а касније у раду Џ.Ј. Силвестера (1883). Понекад принцип се назива формула Да Силве, или Силвестера због ових публикација. Принцип је пример методе сито која се користи у теорији бројева и понекад назива сита формула, иако Легендре већ користи сличан уређај у сито контексту у 1808.

Као коначна вероватноћа рачунају се бројања у односу на кардиналности вероватноће простора, формуле за принцип укључивања-искључивања остају на снази када се кардиналности сетова замени коначном вероватноћом. Уопштено говорећи, обе верзије принципа могу се ставити под заједничким називом теорије мере.

У веома апстрактаном окружењу, принципима укључења-искључења може се изразити као обрачун инверзије матрице. Ова инверзна има посебну структуру, што је изузетно вредна техника у комбинаторици и сродним областима математике. Ђан Карло Рота је рекао:

"Један од најкориснијих принципа набрајања у дискретној вероватноћи и теорији комбинаторике је прослављени принцип укључивања-искључивања. Када се вешто примењује, овај принцип је дао решење за многе комбинаторијалне проблеме"

Изјава

У свом општем облику, принцип укључивања и искључивања тврди да за коначне скупове A₁, ..., A_n, има идентитет

Сваки термин формуле укључивања и искључивања постепено исправља бројање док се сваки део на Веновом дијаграму рачуна тачно једанпут.

Ово се компактно може написати као 

${\Biggl |}\bigcup _{i=1}^{n}A_{i}{\Biggr |}=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leq i_{1}<\cdots <i_{k}\leq n}\left|A_{i_{1}}\cap \cdots \cap A_{i_{k}}\right|\right)$

${\Biggl |}\bigcup _{i=1}^{n}A_{i}{\Biggr |}=\sum _{\emptyset \neq J\subseteq \{1,2,\ldots ,n\}}(-1)^{|J|-1}{\Biggl |}\bigcap _{j\in J}A_{j}{\Biggr |}.$

Речима, да би се рачунао број елемената уније коначних скупова, прво сабрати кардиналности појединачних сетова, а затим одузети број елемената који се појављују у више од једног скупа, затим вратити број елемената који се појављују у више од два скупа, а затим одузети број елемената који се јављају у више од три скупа, и тако даље. Овај процес се завршава природно, јер не може бити елемената који се појављују у више скупова него што има у унији.

У апликацијама је уобичајено да се види принцип изражен у својом комплементарном облику. То јест, остављајући S као коначан универзални скуп који садржи све из  A_i , и допуштајући да ${\bar {A_{i}}}$ означава комплементно A_i у S, по Де Моргановим законима

${\biggl |}\bigcap _{i=1}^{n}{\bar {A_{i}}}{\biggr |}={\biggl |}S-\bigcup _{i=1}^{n}A_{i}{\biggr |}=\left|S\right|\;-\sum _{i=1}^{n}\left|A_{i}\right|\;+\sum _{1\leq i<j\leq n}\left|A_{i}\cap A_{j}\right|\;-\;\ldots \ +\;\left(-1\right)^{n}\left|A_{1}\cap \cdots \cap A_{n}\right|.$

Као још један варијанта изјаве, нека П1, П2, ..., пн бити листа некретнина које елементи скупа С може или не може имати, онда је принцип укључивања и искључивања обезбеђује начин за израчунавање броја елемената од С који имају ништа од имовине. Само нека Ај бити подскуп елемената С који имају имовину Пи и користе принцип у комплементарном облику. Ова варијанта је због Џ.Ј. Силвесте.

Примери

Бројање целих бројева

Као једноставан пример употребе принципа укључивања-искључивања, размотрити питање:

Колико има целих бројева у {1,...,100} који нису дељиви 2, 3 или 5?

S = {1,...,100} и P₁ вредност која је цео број дељив са 3, P₂ вредност која је цео број дељив са 3 и P₃ вредност која је цео број  дељив са 5. Нека је A_i подскуп од S чији су елементи вредности P_i за које имамо |A₁| = 50, |A₂| = 33, и |A₃| = 20. Постоји 16 природних бројева који су дељиви са 6, 10 дељив са 10 и 6 дељив са 15. Коначно, постоје само 3 цела броја дељива са 30, тако да је број целих бројева који нису дељиви са 2, 3 или 5:

100 − (50 + 33 + 20) + (16 + 10 + 6) − 3 = 26.

Бројање пермутација

Следећи пример је мало сложенији.

Претпоставимо да је шпил n карата са  бројевима од 1 до n. Претпоставимо да картица нумерисана м је у исправном положају ако је мј картицу у палуби. На колико начина В се може карта измешати са најмање 1 картом да буде у правилном положају?

Почните са дефинисањем скупа АМ, који је све налоге карата са m картом исправио. Онда је број налога, W, са најмање једном картом која је у правилном положају, m је

$W={\biggl |}\bigcup _{m=1}^{n}A_{m}{\biggr |}.$

Примени принцип укључивања-искључивања,

$W=\sum _{m_{1}=1}^{n}\left|A_{m_{1}}\right|{}-\sum _{1\leq m_{1}<m_{2}\leq n}\left|A_{m_{1}}\cap A_{m_{2}}\right|{}+\sum _{1\leq m_{1}<m_{2}<m_{3}\leq n}\left|A_{m_{1}}\cap A_{m_{2}}\cap A_{m_{3}}\right|{}-\cdots {}+(-1)^{p-1}\sum _{1\leq m_{1}<\cdots <m_{p}\leq n}\left|A_{m_{1}}\cap \cdots \cap A_{m_{p}}\right|\cdots .$

Свака вредност $A_{m_{1}}\cap \cdots \cap A_{m_{p}}$  представља скуп мешања који има најмање р вредности m₁, ..., m_p у правилном положају. Имајте на уму да је број мешања са најмање р вредностима коректним зависимо од р, а не на конкретним вредностима m. На пример, број мешања имају 1., 3. и 17. карте у исправном положају је исти као и број мешања који имају 2., 5. и 13. карте у исправном положају. Једино што је важно да  од n карата, 3 буду изабране у правилном положају. Дакле постоје ${n \choose p}$ једнаких услова при p сабирању (види комбинације).

$W={n \choose 1}\left|A_{1}\right|-{n \choose 2}\left|A_{1}\cap A_{2}\right|+{n \choose 3}\left|A_{1}\cap A_{2}\cap A_{3}\right|-\cdots +(-1)^{p-1}{n \choose p}\left|A_{1}\cap \cdots \cap A_{p}\right|\cdots .$

$\left|A_{1}\cap \cdots \cap A_{p}\right|$ је број наредби које имају р елементе у правилном положају, који је једнак броју начина наредби преосталих n − p елемената (n − p)!. Тако смо коначно добили:

$W={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+{n \choose 3}(n-3)!-\cdots +(-1)^{p-1}{n \choose p}(n-p)!\cdots W=\sum _{p=}^{n}(-1)^{p-1}{n \choose p}(n-p)!.$

Констатујући да  ${n \choose p}={\frac {n!}{p!(n-p)!}}$, ово се смањује на:

$W=\sum _{p=1}^{n}(-1)^{p-1}\,{\frac {n!}{p!}}.$

Пермутација где нема карти  у исправном положају се зове поремећај. Узимајући n! да је укупан број пермутација, вероватноћа Q  насумично  производи пермутације

$Q=1-{\frac {W}{n!}}=\sum _{p=0}^{n}{\frac {(-1)^{p}}{p!}},$

скраћивање за n+1 смислу Тејлорове експанзије e⁻¹. Тако је вероватноћа погађања за мешање шпила карата или била нетачна где је свакој карти 1/е или 37%.

Посебан случај

Ситуација која се појављује у поремећење примеру изнад јавља довољно често да заслужује посебну пажњу. Наиме, када је величина пресек скупова који се појављују у формулама принципа укључивања-искључивања зависи само од броја скупова у пресецима, а не на којем поставља се појављују. Више формално, ако пресек

$A_{J}:=\bigcap _{j\in J}A_{j}$

има исти кардиналност, кажу α_k = |A_J|, за свако k-елемент подгрупа J of {1, ..., n}, а затим

${\biggl |}\bigcup _{i=1}^{n}A_{i}{\biggr |}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\alpha _{k}.$

Или, у комплементарне облику, где универзалног скупа С има кардиналност α₀,

${\biggl |}S\setminus \bigcup _{i=1}^{n}A_{i}{\biggr |}=\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}\alpha _{k}.$

Генерализација

С обзиром на породицу (понављања дозвољено) подскупова A₁, A₂, ..., A_n о универзалној скупу С, принцип укључивања и искључивања израчунава број елемената С у једној од ових подскуповима. Генерализација овог концепта би израчунати број елемената С које се појављују у тачно неки фиксни м ових скупова.

Нека је N = [n] = {1,2,...,n}. Ако дефинишемо $A_{\emptyset }=S$, онда је принцип укључивања и искључивања може бити написан као, користећи нотацију на претходном одељку; број елемената С садржан у једној од A_i је:

$\sum _{J\subseteq [n]}(-1)^{|J|}|A_{J}|.$

Ако је фиксна подскуп скупа индекса Н, онда је број елемената који припадају A_i за све и у И и без других вредности је:

$\sum _{I\subseteq J}(-1)^{|J|-|I|}|A_{J}|.$

Дефинисати скупове

$B_{k}=A_{I\cup \{k\}}$ for k in $N\setminus I$.

Тражимо број елемената у једном од БК који, по принципу укључивања-искључивања (са $B_{\emptyset }=A_{I}$), је

$\sum _{K\subseteq N\setminus I}(-1)^{|K|}|B_{K}|.$

Кореспонденција K ↔ J = I ∪ K имеђу подскупа N \ I  подскупа N који садржи I је бијекција и ако Ј и К одговарају по овој једнјој карти онда B_K = A_J, показује да је резултат важећи

У вероватноћи

У вероватноћи, за догађаје A₁, ..., A_n у вероватноћи простора $\scriptstyle (\Omega ,{\mathcal {F}},\mathbb {P} )$, Принцип укључивања-искључивања постаје за n = 2

$\mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),$

за n = 3

$\mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})\qquad {}-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})\qquad {}+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})$

што може бити написано у затвореној форми као

$\mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{\scriptstyle I\subset \{1,\ldots ,n\} \atop \scriptstyle |I|=k}\mathbb {P} (A_{I})\right),$

Када је последњи сума иде преко свих подгрупе индекса сам 1, ..., нк који садрже елементе тачно, и

$A_{I}:=\bigcap _{i\in I}A_{i}$

означава пресек свих A_i са индексом I.

Према Бонферонијевој неједнакости, збир првих услова у формули је горња граница Алтернативно и доње границе за LHS. Ово се може користити у случајевима када је пуна формула превише гломазна.

За опште мере простори (S,Σ,μ) и мерљиве подгрупе A1, ..., An коначне мере, изнад дна идентитета такође се налази вероватноћа мера $\mathbb {P}$ која је замењена мером μ.

Посебан случај

Ако се у пробабилистичкој верзији принципа укључивање и искључивања, вероватноћа пресека A_I само зависи од I, што значи да за свако k у {1, ..., n} постоји неко a_k такво да

$a_{k}=\mathbb {P} (A_{I})\quad {\text{for every}}\quad I\subset \{1,\ldots ,n\}\quad {\text{with}}\quad |I|=k,$

тада горња формула поједностављује то

$\mathbb {P} {\biggl (}\bigcup _{i=1}^{n}A_{i}{\biggr )}=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}$

због комбинаторног тумачењу биномних коефицијента $\scriptstyle {\binom {n}{k}}$.

Аналогно поједностављење је могуће у случају општа мера простора (S,Σ,μ) и мерљиве подгрупе A₁, ..., A_n крајње мере.

Други облици

Принцип понекад остаје у форми која каже да ако је

$g(A)=\sum _{S\subseteq A}f(S)$

онда је

$f(A)=\sum _{S\subseteq A}(-1)^{\left|A\right|-\left|S\right|}g(S)\qquad (**)$

Сада показати штету и вероватноће комбинаторни верзију за инклузију искључености принципу су случајеви (**). Узети ${\underline {m}}=\{1,2,\ldots ,m\}$, $f({\underline {m}})=0$, и

$f(S)={\bigg |}\bigcap _{i\in {\underline {m}}\backslash S}A_{i}{\bigg \backslash }\bigcup _{i\in S}A_{i}{\bigg |}\qquad {\text{and}}\qquad f(S)=\mathbb {P} {\bigg (}\bigcap _{i\in {\underline {m}}\backslash S}A_{i}{\bigg \backslash }\bigcup _{i\in S}A_{i}{\bigg )}$

респективно за две скупове $S$ са $S\subsetneq {\underline {m}}$. Онда мењамо

$g(A)={\bigg |}\bigcap _{i\in {\underline {m}}\backslash A}A_{i}{\bigg |},~~g({\underline {m}})={\bigg |}\bigcup _{i\in {\underline {m}}}A_{i}{\bigg |}\qquad {\text{and}}\qquad g(A)=\mathbb {P} {\bigg (}\bigcap _{i\in {\underline {m}}\backslash A}A_{i}{\bigg )},~~g({\underline {m}})=\mathbb {P} {\bigg (}\bigcup _{i\in {\underline {m}}}A_{i}{\bigg )}$

респективно за све скупове $A$ са $A\subsetneq {\underline {m}}$. То је зато што елементи $a$ од $\cap _{i\in {\underline {m}}\backslash A}A_{i}$ могу бити укључени у други $A_{i}$ ($A_{i}$ са $i\in A$) тако да $\cap \backslash \!\!\cup \!{\text{-}}$формула Управо пролази кроз сва могућа продужења скупова $\{A_{i}\mid i\in {\underline {m}}\backslash A\}$ са другим $A_{i}$, бројањем $a$ само за скупове који утичу на члан $a$, ако $S$ пролази кроз све подскупове $A$ (као у дефиницји $g(A)$).

Пошто је $f({\underline {m}})=0$, мењамо из (**) са $A={\underline {m}}$ тако да

$\sum _{{\underline {m}}\supseteq T\supsetneq \varnothing }(-1)^{\left|T\right|-1}g({\underline {m}}\backslash T)=\sum _{\varnothing \subseteq S\subsetneq {\underline {m}}}(-1)^{m-\left|S\right|-1}g(S)=g({\underline {m}})$

и преплићу се стране, комбинаторна и пробабилистичка верзија прати принцип укључивања и искључивања.

Ако се посматра број $n$ као скуп својих главних фактора, а затим (**) је генерализација Мобиус инверзије формуле за природне бесквадратне бројеве. Дакле, (**) види као Мобиус инверзија формуле за учесталост алгебре делимично одређеног скупа свих подскупова А.

За генерализација пуној верзији Мобиус инверзија формуле, (**) мора бити генерализована. За више скупова уместо скупова, (**) постаје

$f(A)=\sum _{S\subseteq A}\mu (A-S)g(S)\qquad (***)$

где је $A-S$ виши скуп за свако$(A-S)\uplus S=A$, и

• μ(S) = 1 ако је S скуп (скуп без дуплих елемената) парне кардиналности.
• μ(S) = −1 ако је S скуп (скуп без дуплих елемената) непарне кардиналности.
• μ(S) = 0 ако је S прави (S има дупле елементе).

Узети да је $\mu$$(A-S)$ једнако $(-1)^{\left|A\right|-\left|S\right|}$ of (**) у случају када је $A-S$ скуп.

Доказ (***): Замена

$g(S)=\sum _{T\subseteq S}f(T)$

 на десној страни (***). Приметити да се $f(A)$ појављује на обе стране (***). Морамо показати да за свако  $T$ са $T\subsetneq A$,  $f(T)$ завршава се на десној страни (***). Тако препорављено $T$ тако да $T\subsetneq A$ и узима прозвољно $a\in A$ тако да$a\not \in T$.

Приметити да $A-S$ мора да буде скуп за свако позитивно или негативно појављивање  $f(T)$ на десној страни (***) које се добија од $S$ тако да је $T\subseteq S\subseteq A$. Сада за свако појављивање $f(T)$ на десној страни (***) добија се од $S$ тако да је $A-S$ скуп који укључује $a$ поништава са оним што се добија путем одговарајуће $S$ тако да $A-S$ је скуп који не укључује $a$. Ово ће дати жељени резултат.

Апликације

Принцип укључивања и искључивање је у широкој употреби и овде се само неколико апликација помиње.

Бројање пермутација елемената скупа

Позната примена принципа укључивања и искључивања је комбинаторни проблем рачунајући све поремећаје о коначном скупу. Бројање пермутација елемената скупа А је бијекција из А која нема фиксних тачака. Преко принципа укључивања и искључивања може се показати да ако је кардиналност А једнака n, онда је број поремећајима је [n! / e] где [k] означава најближи цео број x; детаљан доказ је доступан овде и видети одељак примери горе.

Прво појављивање проблема бројање пермутација елемената скупа у раној књизи о играма на срећу: Essai d'analyse sur les jeux de hazard  П. Р. де Монтморта (1678 – 1719) он је био познат као "Монтмортов проблем" или по имену које му је дао "problème des rencontres." Проблем је такође познат као hatcheck проблем.

Број пермутација елемената скупа је познат као субфакторијал од n, написан !n. Из тога следи да ако су све бијекције додељене истој вероватноћи онда је вероватноћа случајне бијекције представља пермутација елемената скупа који приближно као 1/e расте ка n.

Бројање пресека

Принцип укључења и искључења комбинован са Де Моргановим законима, може се користити да се изброји кардиналност пресека скупова. Нека $\scriptstyle {\overline {A}}_{k}$ представља допуну A_k у односу на неки универзални скуп А тако да је $\scriptstyle A_{k}\,\subseteq \,A$ за свако k. Затим имамо

$\bigcap _{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A}}_{i}}}$

 окретање проблема проналажења пресека у проблем проналажења уније.

Граф колорита

Принцип искључења укључења чини основу алгоритама за бројне НП-тешке графове преградних проблема, као што су графови колорита.

Добро позната примена принципа је изградња хроматског полинома графа.

Бипартициони график савршених поклапања

Број савршених поклапања бипартиционог графика може бити израчунат користећи овај принцип.

Број "на" функције

С обзиром на коначне скупове А и В, колико сирјективних функција (на функцијама) постоји од А до Б? Без икаквог губитка општости можемо узети А = {1,2, ..., k} и В = {1,2, ..., n}, јер је само кардиналности скупова битна. Коришћењем S као скупа свих функција од А до B, и дефинисање, за свако  i у B, Pi као "функција којој недостаје елемент  i у B" ( i није у слици функције), принцип укључивања и искључивања даје број "на" функција између А и B као:

$\sum _{j=0}^{n}{\binom {n}{j}}(-1)^{j}(n-j)^{k}.$

Пермутације са забрањеним позицијама

Пермутација скупа S = {1,2, ..., n} где је сваки елемент S ограничен да не буде у одређеним позицијама (овде пермутација се сматра наручивање од елемената S) назива се пермутација са забрањеним местима. На пример, са S = {1,2,3,4}, пермутације уз ограничење да елемент 1 не може бити на позицијама 1 или 3, и елемент 2 не може бити на позицији 4 су: 2134, 2143, 3124, 4123, 2341, 2431, 3241, 3421, 4231 и 4321. Дајући  да Аi буде скуп ставова који елементу i нису дозвољени да буду у скупу, а Pi да је имовина која пермутација ставља елемент сам у позицију Ai, принцип укључивања и искључивања може да се користи да рачунају број пермутација које задовољавају сва ограничења.

У датом примеру, дато је 12 = 2(3!) пермутација са P₁, 6 = 3! пермутација са P₂ и нема пермутација за P₃ илиP₄ јер не постоје ограничења за ова два елемента. Број пермутација задовољавају ограничења је овако:

4! − (12 + 6 + 0 + 0) + (4) = 24 − 18 + 4 = 10.

Коначно 4 у овој компилацији је број пермутација које имају оба својства P₁ i P₂. Нема других не-нула доприноса формули.

Стирлинг бројеви друге врсте

Стирлинг бројеви друге врсте, S (n, k) израчуна број партиција скупа n елемената у k непразним подскуповима (неразазнатљиве кутије). Експлицитна формула за њих се може добити применом принципа укључивања-искључивања у веома блиско повезаном проблем, наиме, рачунајући број партиција од n-скупа у k непразном али се разликују кутије (уређеним непразним подскуповима). Коришћење универзалног скупа који се састоји од свих партиција на n-скупу у k(вероватно празан) препознатљиве кутије,  A₁, A₂, ..., A_k, и својства Pi што значи да партиција има кутију Ai празан, принцип укључивања и искључивања даје одговор за који се односи резултат. Подела од k! да уклони вештачку редослед даје Stirling број друге врсте:

$S(n,k)={\frac {1}{k!}}\sum _{t=0}^{k}(-1)^{t}{\binom {k}{t}}(k-t)^{n}.$

Топ полиноми

Топ полином је генерисање функција на више начина да се пласирају у не-напад топова на табли В која изгледа као подскуп квадрата са шаховске табле; то јест, не постоје два топа која могу бити у истом реду или колони. Одбор В  је било који подскуп од квадрата правоугаоног одбора са n редова и колона n; ми мислимо о томе као о квадрату у којем је једном дозвољено да стави топа. Коефицијент, r_k(B) од x^k у топу полиномаR_B(x) је број начина k топова, од којих ниједан не напада другог, да се могу организовати у трговима B. За било који одбора B, постоји комплементарни одбор B "који се састоји од квадрата правоугаоног одбора који нису у B, ова комплементарна плоча има топа полинома R_B' (x) са коефицијентима r_k(B').

Понекад је згодно да би могао да израчуна највиши коефицијент топа полинома у смислу коефицијената полинома топа комплементарног одбора. Без губитка општости можемо претпоставити да је n ≤ m, па је коефицијент r_n(B). Број начина да поставите n који не нападају топове на  n × m табли (без обзира о томе да ли су смештени у топу квадрата на плочи Б) је дат као факторијелски пад:

$(m)_{n}=m(m-1)(m-2)\cdots (m-n+1).$

Пустити да P_i има задатак n не напада топова на комплетној табли има топа у колумни  i која није у квадрату табле Б, онда по принципу укључивања и искључивања имамо:

$r_{n}(B)=\sum _{t=0}^{n}(-1)^{t}(m-t)_{n-t}\;r_{t}(B').$

Ојлерова фи функција

Ојлерова фи функција, φ(n) је аритметичка функција која пребројава позитивне целе бројеве мање или једнаке n који су релативно прост са n. То јест, ако је  n позитиван  број, онда  φ(n) је број бројева k у домену 1 ≤ k ≤ n које немају заједнички фактор са n осим 1. Принцип укључивања и искључивања се користи за добијање формуле φ(n). Нека је S скуп  {1,2,...,n} и дефинише P_i као број у скупу S који је дељив са простим бројем p_i, за 1 ≤ i ≤ r, где је растављање на факторе од 

$n=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{r}^{a_{r}}.$

Онда,

$\phi (n)=n-\sum _{i=1}^{r}{\frac {n}{p_{i}}}+\sum _{1\leq i<j\leq r}{\frac {n}{p_{i}p_{j}}}-\cdots =n\prod _{i=1}^{r}\left(1-{\frac {1}{p_{i}}}\right).$

Ублажени принцип укључења и искључења

У многим случајевима где би принцип могао дати тачну формулу (посебно, рачунајући просте бројеве користећи Ератостеново сито), формула која произилази не нуди корисне садржаје јер је број термина у њој претеран. Ако се сваки термин појединачно може прецизно проценити, акумулација грешака може да имплицира да формула укључивања и искључивања није директно примењива. У теорији бројева, ову тешкоћу разматрао је Виго Бран. Након спорог почетка, његове идеје су предузете од стране других, и метода сита је развијена. На пример може покушати да нађе горњу границу за "прошаране" скупове, а не тачну формулу.

Нека су A₁, ..., A_n произвољни скупови и  p₁, ..., p_n реални бројеви у затвореном интервалу [0,1]. Онда за сваки паран број k у {0, ..., n}, индикатор функције задовољава неједнакост:

$1_{A_{1}\cup \cdots \cup A_{n}}\geq \sum _{j=1}^{k}(-1)^{j-1}\sum _{1\leq i_{1}<\cdots <i_{j}\leq n}p_{i_{1}}\dots p_{i_{j}}\,1_{A_{i_{1}}\cap \cdots \cap A_{i_{j}}}.$

Ако је k паран, заменити  "≥" са "≤".

Доказ главне изјаве

Изаберите елемент садржан у уједињење свих скупова и нека $A_{1},A_{2},\dots ,A_{t}$ бити индивидуални сетови који га садрже. (Имајте на уму да Т> 0.) Пошто је елемент броји управо једном од левој страни једначине (1), морамо да покажемо да се рачуна управо једном од десне стране. Са десне стране, једини не-зеро доприноси јављају када су све Подскупови у одређеном року садрже изабрани елемент, то јест, сви подскупови су одабрана од$A_{1},A_{2},\dots ,A_{t}$. Допринос је један за сваки од ових сетова (плус или минус у зависности од термина) и зато је само (потписао) број ових подскупова који се користе у року. Онда имамо:

По биномној теореми,

$0=(1-1)^{t}={\binom {t}{0}}-{\binom {t}{1}}+{\binom {t}{2}}-\cdots +(-1)^{t}{\binom {t}{t}}$.

Користећи се чињеницом да је  ${\binom {t}{0}}=1$ и преуређењем услова, имамо

$1={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}},$

and so, the chosen element is counted only once by the right-hand side of equation (1).

Алгебарски доказ

Алгебарски доказ може се добити помоћу функције индикатора (карактеристичне функције подскупова скупа). Индикатор функција подскупа S скупа X је функција

$\mathbf {1} _{S}\colon X\to \{0,1\}\,$

дефинисано као

$\mathbf {1} _{S}(x):={\begin{cases}1&{\text{if }}x\in S,\\0&{\text{if }}x\notin S.\end{cases}}$

Писање слагања два индикатора функције као производа, имамо да, ако су $A$ и $B$ подскупови $X$, онда је

$\mathbf {1} _{A}\cdot \mathbf {1} _{B}=\mathbf {1} _{A\cap B}.$

Нека А означава унију  ${\textstyle \cup _{i=1}^{n}A_{i}}$ скупова A₁, ..., A_n. Да би се доказао принцип укључења и искључења у потпуности, прво се провери идентитет

за индикатор функције, где је

$A_{I}=\bigcap _{i\in I}A_{i}.$

Следећа функција је једнака нули

$(1_{A}-1_{A_{1}})(1_{A}-1_{A_{2}})\cdots (1_{A}-1_{A_{n}})\,=\,0,$

јер: ако је х није у А, онда сви су фактори 0 - 0 = 0; и на други начин, ако х не припада неком  A_m онда одговарајући m фактор је 1 - 1 = 0. проширење производа на левој страни, једначина (*) следи.

Да би доказао принцип укључења и искључења за кардиналност скупова, сумирамо једначине (*) над свим х у унији A₁, ..., A_n. За извођење верзије коришћене у вероватноћи, узми очекивања у (*). У принципу, интегришите једначину (*) у односу на μ. Увек користите линеарност у овим извођењима.

Види још

• Принципи комбинаторике
• Булова неједнакост
• Проблем огрлице
• Schuette–Nesbitt формула
• Идентитети максимум и минимум

Литература

• Allenby, R.B.J.T.; Slomson, Alan . How to Count: An Introduction to Combinatorics, Discrete Mathematics and Its Applications (2 ed.). . CRC Press. 2010. pp. 51–60. ISBN 978-1-4200-8260-9. 
• Björklund, Andreas; Husfeldt, Thore; Koivisto, Mikko (2009). „Set Partitioning via Inclusion-Exclusion”. SIAM Journal on Computing. 39 (2): 546—563. doi:10.1137/070683933. 
• Brualdi, Richard A. (2010). Introductory Combinatorics (5th изд.). Prentice–Hall. ISBN 978-0-13-602040-0. 
• Cameron, Peter J. (1994). Combinatorics: Topics, Techniques, Algorithms. Cambridge University Press. ISBN 978-0-521-45761-3. 
• Fernández, Roberto; Fröhlich, Jürg; Alan D., Sokal (1992). Random Walks, Critical Phenomena, and Triviality in Quantum Field Theory. Texts an Monographs in Physics, Berlin: Springer-Verlag. ISBN 978-3-540-54358-9.  MR 1219313, Zbl 0761.60061
• Graham, R.L.; Grötschel, M.; Lovász, L. (1995). Hand Book of Combinatorics. 2. MIT Press – North Holland. ISBN 978-0-262-07171-0. CS1 одржавање: Вишеструка имена: списак аутора (веза)
• Gross, Jonathan L. (2008). Combinatorial Methods with Computer Applications. Chapman&Hall/CRC. ISBN 978-1-58488-743-0. 
• Hazewinkel, Michiel , "Inclusion-and-exclusion principle", ур. (2001). Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4. CS1 одржавање: Вишеструка имена: списак уредника (веза)
• Mazur, David R. (2010). Combinatorics A Guided Tour. The Mathematical Association of America. ISBN 978-0-88385-762-5. 
• Roberts, Fred S.; Tesman, Barry (2009). Applied Combinatorics (2nd изд.). CRC Press. ISBN 978-1-4200-9982-9. 
• {{Cite book| ref=harv|last=Stanley|first=Richard P.|title=Enumerative Combinatorics Volume I|location=|publisher=Wadsworth & Brooks/Cole|year=1986|isbn=978-0-534-06546-1|pages=}
• van Lint, J.H.; Wilson, R. M. (1992). A Course in Combinatorics. Cambridge University Press. ISBN 978-0-521-42260-4. 

This article incorporates material from principle of inclusion–exclusion on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.