Хафманови кодови

У области комуникација и рачунарске технике, Хафманово кодирање представља алгоритам за кодирање симбола без губитка информација. Иако је Хафманово кодирање врло ефикасно постоје алгоритми који користе релације између појединих симбола и на тај начин побољшавају ефикасност алгоритма. Хафманов код се базира на редунданси по којој се одређени карактери чешће јављају од осталих. Хафманови кодови редукују број битова који се шаљу, али је код њих неопходно знати ведност вероватноће појављивања.

Историјат

Хафманов алгоритам је настао 1953. Развио га је Дејвид Хафман док је био на докторским студијама на МИТ и објавио у раду "A Method for the Construction of Minimum-Redundancy Codes".

Хафманов алгоритам

Циљ Хафмановог алгоритма је минимизација тежинске екстерне дужине пута што у ствари представља збир производа нивоа и тежина за све екстерне чворове стабла.

Хафманов алгоритам креће од шуме х стабала са по једним екстерним чвором. У свакој итерацији из реда у коме се налазе стабла ваде се два корена са најмањим тежинама, затим се прави чвор са тежином која је једнака збиру тежина изабраних чворова. Сада је новонастали чвор корен новог стабла чији су лево и десно подстабло изабрана два чвора. Новонастало стабло се сада враћа у ред и у новим итерацијама конкурише равноправно са осталим стаблима. У свакој новој итерацији се узимају нова два корена од којих се прави ново стабло са кореном чија је тежина једнака збиру тежина корена изабраних стабала. Овако се у свакој итерацији смањује број стабала за један све док у реду не остане само једно стабло. Ако на почетку имамо шуму од х стабала, потребна нам је х-1 итерација да би добили крајње стабло. Овакво стабло има корен чија је тежина једнака збиру тежина свих екстерних чворова који су се на почетку налазили у реду, а који такође сада чине листове новонасталог стабла. Овако настало стабло има минималну тежинску екстерну дужину пута.

Ово је похлепни алгоритам и може се генерализовати и на стабла вишег реда. С обзиром да у реду може постојати више елемената са истом тежином онда може постојати и више стабала са истом минималном тежинском екстерном дужином пута. Међутим ако желимо да добијемо стабло које уједно има и најмању висину стабла онда елементе са истом тежином треба да уклањамо по FIFO редоследу.

Ово стабло служи као модел доношења бинарних одлука. Листови су коначне одлуке и не долази се до свих истом вероватноћом. Стабло реализује оптималну процедуру одлучивања.

Сложеност алгоритма је у најбољем случају О(хlog х). Сложеност зависи од имплементације реда и најефикасније је када се ред имплементира као бинарни heap.

Хафманови кодови

Користе се за компресију података. Компресијом података приликом чувања или преноса се штеди на меморији. Један од примера су поруке које чине азбучна слова. Приликом кодовања поруке мора се водити рачуна да процеси кодовања и декодовања буду једноставни, а опет дужина поруке треба да буде минимална. Сваки симбол се представља неким бинарним кодом. Сада се за сваки симбол мора одредити вероватноћа Рх. У овом случају је најбоље да то буде вероватноћа појављивања датог симбола. Збир свих вероватноћа мора наравно да буде 100. Сваки знак може да има произвољан код. Због лаког декодовања користе се префиксни кодови. То значи да код ни једног симбола не сме да се користи као почетак кода неког другог симбола. Процес декодовања се сада своди на то да се креће од почетка бинарне секвенце и узима онолико знакова колико је потребно да се добије валидан код.

Префиксни кодови се добијају применом Хафмановог алгоритма па се такви кодови још називају и Хафмановим кодовима. Сада сваки симбол представља екстерни чвор који се ставља у ред и од којих се гради стабло. Тежине ових чворова су, у ствари, њихове вероватноће појављивања. У стаблу добијеном применом Хафмановог алгоритма листови су задати симболи. Бинарни код сваког симбола добија се као путања од корена до тог симбола тако што сваки пут када се иде улево подстабло неког чвора у код се убацује 0, а када се иде удесно подстабло у бацује се 1. У бинарном стаблу пут до сваког екстерног чвора је јединствен па смо тиме обезбедили да добијени кодови буду префиксни

Особине Хафмановог кодирања

Хафманово кодирање проналази оптималан систем кодирања заснован на релативној вероватноћи појављивања сваког елемента. Представља ентропијско кодирање симбола без губитка информација. Хафманово кодирање је најефикаснији метод компресије симбола који нису у тесном односу, у својој класи. Он припада класи пресликавања карактера неке текстуалне колекције у битове за познате вероватноће појављивања сваког карактера. Најдужи Хафманов код се добија када се дистрибуција вероватноћа појављивања одвија по правилу генерисања Фибоначијевих бројева.

Врсте Хафмановог кодирања

На основу тога да ли су вероватноће појављивања симбола познате унапред или се динамички добијају током извршавања алгоритма, Хафманов алгоритам се дели на статички и динамички.

Статичко Хафманово кодирање

На почетку се гради табела вероватноћа појављивања знакова које кодирамо. Табела треба да буде уређена. Карактери који се чешће јављају кодирају се краћим секвенцама, а они који се ређе користе кодирају се дужим секвенцама. Сада се примењује Хафманов алгоритам на основу табеле.

Динамичко Хафманово кодирање

За разлику од статичког кодирања где се табела вероватноћа појављивања знакова одређује на почетку рада алгоритма код динамичког се вероватноће појављивања израчунавају и мењају динамички у току рада алгоритма.

Пример рада алгоритма

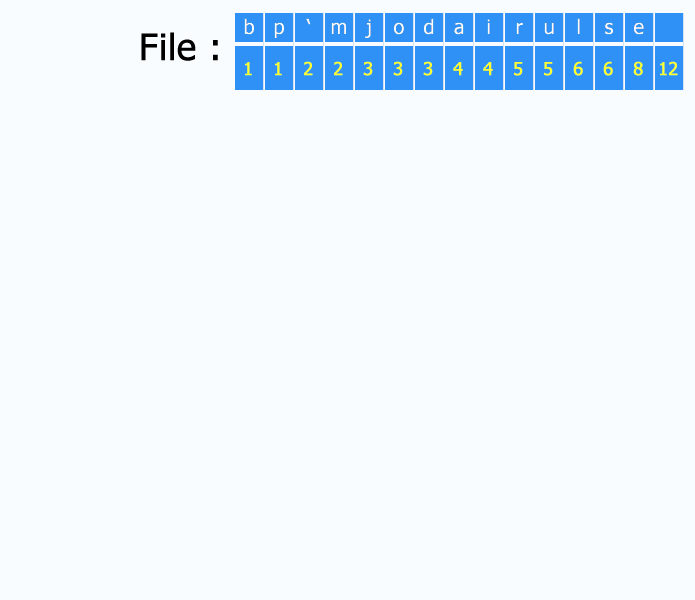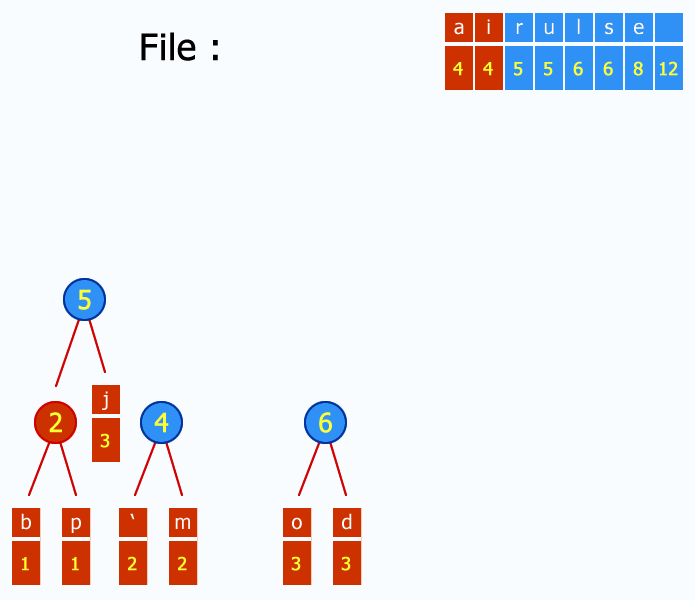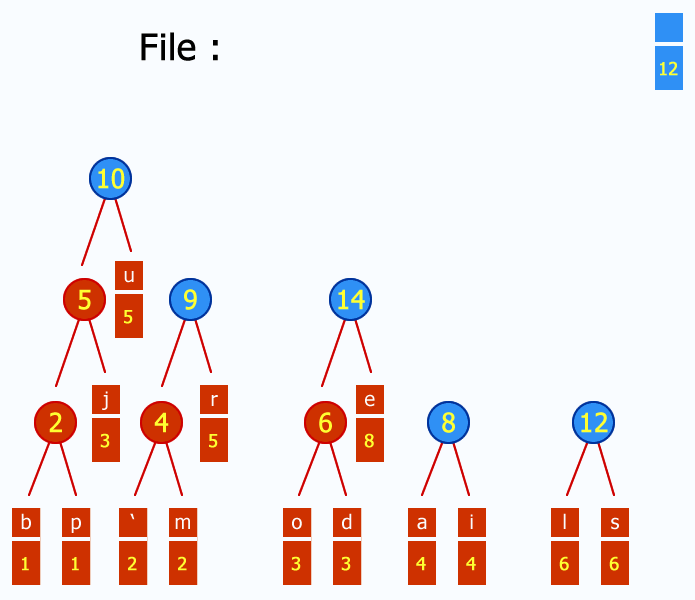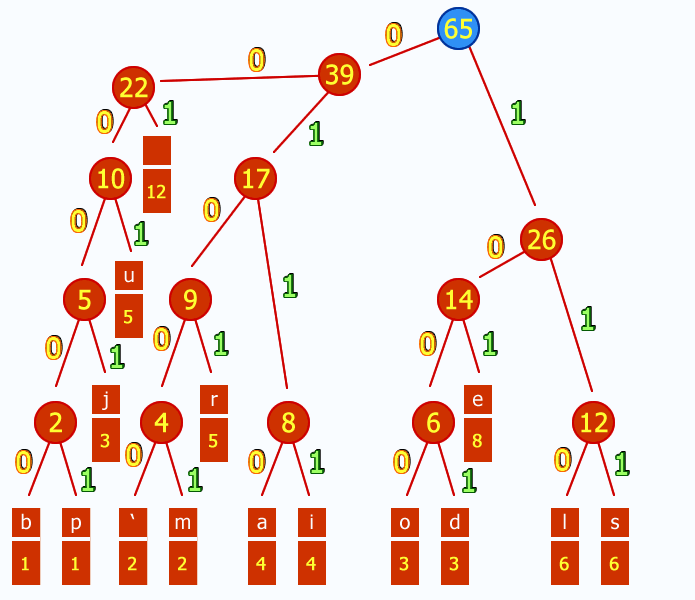
Литература

D.A. Huffman, "A Method for the Construction of Minimum-Redundancy Codes", Proceedings of the I.R.E., September (1952). стр. 1098–1102. Huffman's original article.
Ken Huffman. Profile: David A. Huffman, Scientific American, September (1991). стр. 54–58
Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest & Clifford Stein (2001). Introduction to Algorithms. Second Edition. MIT Press and McGraw-Hill. ISBN 0-262-03293-7. Section 16.3. стр. 385–392.

Спољашње везе