Сабирање Минковског

У геометрији збир Минковског (такође познат као дилација) два скупа позиционих вектора А и В у Еуклидовом простору формира се додавањем сваког вектора у А сваком вектору у В тј скуп
Аналогно, разлика Минковског дефинише се на следећи начин



Пример
[уреди | уреди извор]На пример, ако имамо два скупа А и В, при чему се сваки од њих састоји из три позициона вектора (неформално речено, три тачке), који представљају углове два троуглова у , са координатама
- A = {(1, 0), (0, 1), (0, −1)}
и
- B = {(0, 0), (1, 1), (1, −1)} ,
онда је збир Минковског A + B = {(1, 0), (2, 1), (2, −1), (0, 1), (1, 2), (1, 0), (0, −1), (1, 0), (1, −2)} , што изгледа као шестоугао, са три 'поновљене' тачке (1, 0).
За збир Минковског, нулти скуп;{0}, који садржи само нулти вектор 0, представља неутрални елемент: за сваки подскуп S векторског простора
- S + {0} = S;
Празан скуп је важан код сабирања Минковског зато што сваки празан скуп поништава сваки други подскуп - за сваки други подскуп S, векторског простора, његов збир са празним скупом је празан: S + = .

![Three squares are shown in the non-negative quadrant of the Cartesian plane. The square Q1=[0,1]×[0,1] is green. The square Q2=[1,2]×[1,2] is brown, and it sits inside the turquoise square Q1+Q2=[1,3]×[1,3].](http://upload.wikimedia.org/wikipedia/commons/thumb/d/de/Minkowski_sum.png/220px-Minkowski_sum.png)
Конвексни омотачи збира Минковског
[уреди | уреди извор]Сабирање Минковског понаша се добро у случају поступка узимања конвексних омотача што је приказано у следећој тврдњи:
- За све подскупове S1 и S2 реалног векторског простора, конвексни омотач њихових збирова представља збир њихових конвексних омотача
- Conv(S1 + S2) = Conv(S1) + Conv(S2).
Овај резултат важи уопштење за сваки коначни низ скупова који нису празни
- Conv(∑Sn) = ∑Conv(Sn).
У математичкој терминологији, операције сабирања Минковског и формирања конвексних омотача представљају операције замене.[1][2]
Ако је S конвексни скуп је конвексни сет; онда
- за сваки .
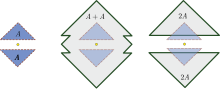
Обрнуто, ако ова „дистрибутивна карактеристика" важи за све реалне бројеве који нису негативни, , онда је скуп конвексан.[3] Фигура приказује пример неконвексног скупа за који је A + A ≠ 2A.
Суме Минковског се понашају линеарно на спољној линији дводимензионалних конвексних тела: спољна линија тог збира једнака је збиру спољнјих линија. Уз то, ако је K (унутрашњост) крива константне ширине, онда је збир K и његове ротације за 180 степени диск. Ове 2 чињенице могу се комбиновати и дати кратак доказ Барбијеве теореме о спољним линијама константне сфере.[4]
Примене
[уреди | уреди извор]Сабирање Минковског игра средишњу улогу у математичкој морфологији. Оно се појављује код парадигме потеза 2D компјутерске графике (са разним применама, нарочито код Доналда Е.Кната у Мегафонту), као и код операције померања тачака код чврстог тела код 3D компјутерске графике.
Планирање кретања
[уреди | уреди извор]Збирови Минковског користе се код планирања кретања предмета између препрека. Користе се за рачунање конфигурационих простора, који представљају скуп присутних позиција предмета. Код просторног модела транслационог кретања једног предмета у авиону, где позиција предмета може бити јединствено дефинисана позицијом једне фиксне тачке овог предмета, конфигурациони простор представљаја збир Минковског скупа препрека и покретног предмета постављеног на почетку и ротираног за 180 степени.
Нумеричка контрола (NC) рада машина
[уреди | уреди извор]Код нумеричке контроле рада машина, програмирање NC алатке базира се на чињеници да збир Минковског алатке за сечење са њеном путањом даје облик исечку у материјалу.
Алгоритми за рачунање Минковсковог збира
[уреди | уреди извор]
Пример у равни
[уреди | уреди извор]Два конвексна многоугла у равни
[уреди | уреди извор]За два конвексна многоугла P и Q у равни са угловима m и n, њихов збир је једнак је конвексном многоуглу са највише m + n угловима и може се израчунати у времену O (m + n) веома једноставним поступком, Претпоставимо да су дате ивице многоугла. Претпоставимо да су дате ивице многоугла, а смер је нпр. у смеру казаљке на сату дуж границе многоугла. Онда се лако види да ове ивице конвексног многоугла одређује угао дводимензионалног координатног система. Хајде сад да убацимо одређене распореде усмерених ивица из P и Q у један одређени распоред S. Замислимо да су те ивице чврсте стрелице које се могу слободно кретари док истовремено иду паралелно свом првобитном правцу. Склопимо те стрелице у ред редоследа S везујући крај следеће стрелицеза почетак претходне. Произилази да ће резултујући многоугаони ланац у ствари бити конвексни многоугао који је збир Минковског P и Q.
Остало
[уреди | уреди извор]Ако је један многоугао конвексан, а други није, комплексност њиховог збира Минковског је O(nm). Ако су оба неконвексна, комплексност њиховог збира је O((mn)2).
Основни збир Минковског
[уреди | уреди извор]Постоји такође и појам основног збира Минковског +e два подскупа Еуклидовог простора. Уобичајени збир Минковског се може забележити као
Тако се основни збир Минковског дефинише овако
где μ означава n-димензионалну Лебескову меру. Разлог за термин "основни" леђи у следећој одлици индикаторске функције: док је
може се видети као
где "ess sup" означава основни супремум.
Референце
[уреди | уреди извор]- ^ Theorem 3 (pages 562–563): Krein, M.; Šmulian, V. (1940). „On regularly convex sets in the space conjugate to a Banach space”. Annals of Mathematics (2), Second series. 41. стр. 556—583. JSTOR 1968735. MR 2009. doi:10.2307/1968735.
- ^ For the commutativity of Minkowski addition and convexification, see Theorem 1.1.2 (pages 2–3) in Schneider; this reference discusses much of the literature on the convex hulls of Minkowski sumsets in its "Chapter 3 Minkowski addition" (pages 126–196): Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. стр. xiv+490. ISBN 978-0-521-35220-8. MR 1216521.
- ^ Chapter 1: Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. стр. xiv+490. ISBN 978-0-521-35220-8. MR 1216521.
- ^ The Theorem of Barbier (Java) at cut-the-knot.
Литература
[уреди | уреди извор]- Arrow, Kenneth J.; Hahn, Frank H. (1980). General competitive analysis. Advanced textbooks in economics. 12 (reprint of (1971) San Francisco, CA: Holden-Day, Inc. Mathematical economics texts. 6 изд.). Amsterdam: North-Holland. ISBN 978-0-444-85497-1. MR 439057.
- Gardner, Richard J. (2002), „The Brunn-Minkowski inequality”, Bull. Amer. Math. Soc. (N.S.), 39 (3): 355—405 (electronic), doi:10.1090/S0273-0979-02-00941-2
- Green, Jerry; Heller, Walter P. (1981). „1 Mathematical analysis and convexity with applications to economics”. Ур.: Arrow, Kenneth Joseph; Intriligator, Michael D. Handbook of mathematical economics, Volume I. Handbooks in economics. 1. Amsterdam: North-Holland Publishing Co. стр. 15—52. ISBN 978-0-444-86126-9. MR 634800. doi:10.1016/S1573-4382(81)01005-9. Архивирано из оригинала 17. 12. 2012. г. Приступљено 15. 05. 2014.
- Mann, Henry (1976), Addition Theorems: The Addition Theorems of Group Theory and Number Theory (Corrected reprint of 1965 Wiley изд.), Huntington, New York: Robert E. Krieger Publishing Company, ISBN 978-0-88275-418-5 Спољашња веза у
|publisher=(помоћ) - Rockafellar, R. Tyrrell (1997). Convex analysis. Princeton landmarks in mathematics (Reprint of the 1979 Princeton mathematical series 28 изд.). Princeton, NJ: Princeton University Press. стр. xviii+451. ISBN 978-0-691-01586-6. MR 1451876. MR274683.
- Nathanson, Melvyn B. (1996), Additive Number Theory: Inverse Problems and Geometry of Sumsets, GTM, 165, Springer, Zbl 0859.11003.
- Oks, Eduard; Sharir, Micha (2006), „Minkowski Sums of Monotone and General Simple Polygons”, Discrete and Computational Geometry, 35 (2): 223—240, doi:10.1007/s00454-005-1206-y.
- Schneider, Rolf (1993), Convex bodies: the Brunn-Minkowski theory, Cambridge: Cambridge University Press.
- Tao, Terence & Vu, Van (2006), Additive Combinatorics, Cambridge University Press.










![{\displaystyle A+_{\mathrm {e} }B=\{z\in \mathbb {R} ^{n}\,|\,\mu \left[A\cap (\{z\}-B)\right]>0\},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3808b9e4358326d4b9f89c3013d17e075d8aa552)

