Тригонометријске функције су функције угла . Добиле су име по грани математике која их користи за решавање троуглова , а која се назива тригонометрија .
Када је угао, дакле аргумент ових функција реалан број , тада су то функције равнинске тригонометрије : синус и косинус , од којих се изводе све остале. Од осталих основних функција угла често су у употреби тангенс , па и котангенс , затим, мало ређе се срећу косеканс и секанс , и коначно најређе синус версус и косинус версус . Када је угао комплексан број тада функције угла могу прећи у хиперболичке функције .
Инверзне тригонометријске функције зову се циклометријске функције и аркус-функције , тј. функција-1 .
Сл.1. Тригонометријски троугао Основне тригонометријске функције синус, косинус и тангенс се обично дефинишу помоћу правоуглог троугла , слика десно.
x
=
r
⋅
cos
ϕ
,
y
=
r
⋅
sin
ϕ
,
y
x
=
tg
ϕ
.
{\displaystyle x=r\cdot \cos \phi ,\;y=r\cdot \sin \phi ,\;{\frac {y}{x}}=\operatorname {tg} \phi .}
Позитиван математички угао има супротан смер од казаљке на сату, слично као и кретање Сунца у односу на сунчеву сенку на слици 2.
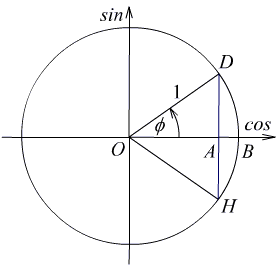
На слици (3) доле је кружница полупречника један са центром у исходишту, тј.
x
2
+
y
2
=
1
,
{\displaystyle x^{2}+y^{2}=1,}
тригонометријска кружница .
У следећој дефиницији и теореми (1), тангенс и котангенс (б) се у англосаксонским земљама означавају tan и cot, косеканс (в) се и код нас означава cosec.
Сл.3. Тригонометријска кружница Дефиниција 1
Тригонометријске реалне функције угла φ дефинишу се једнакостима
(а)
cos
2
ϕ
+
sin
2
ϕ
=
1
,
{\displaystyle \cos ^{2}\phi +\sin ^{2}\phi =1,\,}
синус и косинус су реални бројеви ;(б)
tg
ϕ
=
sin
ϕ
cos
ϕ
,
ctg
ϕ
=
cos
ϕ
sin
ϕ
,
{\displaystyle \operatorname {tg} \phi ={\frac {\sin \phi }{\cos \phi }},\;\operatorname {ctg} \phi ={\frac {\cos \phi }{\sin \phi }},}
тангенс и котангенс ;(в)
sec
ϕ
=
1
cos
ϕ
,
csc
ϕ
=
1
sin
ϕ
,
{\displaystyle \sec \phi ={\frac {1}{\cos \phi }},\;\csc \phi ={\frac {1}{\sin \phi }},}
секанс и косеканс .(г)
vercos
ϕ
=
1
−
sin
ϕ
,
versin
=
1
−
cos
ϕ
,
{\displaystyle \operatorname {vercos} \phi =1-\sin \phi ,\;\operatorname {versin} =1-\cos \phi ,}
косинус версус и синус версус .Функције (в), а нарочито (г) ретко срећемо.
Теорема 1 (а)
O
A
¯
=
cos
ϕ
,
O
C
¯
=
sin
ϕ
,
{\displaystyle {\overline {OA}}=\cos \phi ,\;{\overline {OC}}=\sin \phi ,}
(б)
B
E
¯
=
tg
ϕ
,
F
G
¯
=
ctg
ϕ
,
{\displaystyle {\overline {BE}}=\operatorname {tg} \phi ,\;{\overline {FG}}=\operatorname {ctg} \phi ,}
(в)
O
E
¯
=
sec
ϕ
,
O
G
¯
=
csc
ϕ
,
{\displaystyle {\overline {OE}}=\sec \phi ,\;{\overline {OG}}=\csc \phi ,}
Доказ
Тачка Т са слике 1. овде (сл.2.) је тачка D.
(а) Следи непосредно због полупречника r = 1.(б) Уочимо сличне троуглове
Δ
E
B
O
∼
Δ
D
A
O
,
{\displaystyle \Delta EBO\sim \Delta DAO,}
B
E
¯
:
O
B
¯
=
A
D
¯
:
O
A
¯
,
{\displaystyle {\overline {BE}}:{\overline {OB}}={\overline {AD}}:{\overline {OA}},}
B
E
¯
:
1
=
sin
ϕ
:
cos
ϕ
;
{\displaystyle {\overline {BE}}:1=\sin \phi :\cos \phi ;}
Δ
G
F
O
∼
Δ
O
A
D
,
{\displaystyle \Delta GFO\sim \Delta OAD,}
F
G
¯
:
F
O
¯
=
O
A
¯
:
A
D
¯
,
{\displaystyle {\overline {FG}}:{\overline {FO}}={\overline {OA}}:{\overline {AD}},}
F
G
¯
:
1
=
cos
ϕ
:
sin
ϕ
.
{\displaystyle {\overline {FG}}:1=\cos \phi :\sin \phi .}
(в) Из истих сличних троуглова (б) добијамо
O
E
¯
:
O
B
¯
=
O
D
¯
:
O
A
¯
,
{\displaystyle {\overline {OE}}:{\overline {OB}}={\overline {OD}}:{\overline {OA}},}
O
E
¯
:
1
=
1
:
cos
ϕ
;
{\displaystyle {\overline {OE}}:1=1:\cos \phi ;}
O
G
¯
:
O
F
¯
=
O
D
¯
:
A
D
¯
,
{\displaystyle {\overline {OG}}:{\overline {OF}}={\overline {OD}}:{\overline {AD}},}
O
G
¯
:
1
=
1
:
sin
ϕ
.
{\displaystyle {\overline {OG}}:1=1:\sin \phi .}
Крај доказа.
Овде ће бити анализиране особине вредности тригонометријских функција за посебне углове.
На претходној слици (3) представљен је Декартов правоугли систем координата и тачка D на тригонометријској кружници. Угао BOD = φ може неограничено расти док покретни крак угла (OD) пролази редом кроз први, други, трећи и четврти квадрант , а затим поново по истом кругу . Дакле, угао φ може расти до 360° и даље. При томе се пројекције тачке D на апсцису и ординату увек рачунају као косинус и синус угла φ. То значи да је косинус позитиван када је тачка D у првом и четвртом квадранту, а да је синус позитиван када је тачка D у првом и другом квадранту. Детаљно то видимо у следећој табели:
Тригонометријске функције по квадрантима
Квадрант
1. (0°-90°)
2. (90°-180°)
3. (180°-270°)
4. (270°-360°)
синус
+
+
-
-
косинус
+
-
-
+
тангенс
+
-
+
-
Лако је преко тригонометријске кружнице или адиционих формула проверити тачност формула за свођење вредности тригонометријских функција на функције углова из првог квадранта:
cos
(
180
o
−
ϕ
)
=
−
cos
ϕ
,
sin
(
180
o
−
ϕ
)
=
sin
ϕ
,
{\displaystyle \cos(180^{o}-\phi )=-\cos \phi ,\;\sin(180^{o}-\phi )=\sin \phi ,}
cos
(
180
o
+
ϕ
)
=
−
cos
ϕ
,
sin
(
180
o
+
ϕ
)
=
−
sin
ϕ
,
{\displaystyle \cos(180^{o}+\phi )=-\cos \phi ,\;\sin(180^{o}+\phi )=-\sin \phi ,}
cos
(
−
ϕ
)
=
cos
ϕ
,
sin
(
−
ϕ
)
=
−
sin
ϕ
.
{\displaystyle \cos(-\phi )=\cos \phi ,\;\sin(-\phi )=-\sin \phi .}
Функције косинус и синус су периодичне са основним периодом 360°, a функција тангенс је периодична са периодом 180°:
cos
(
360
o
+
ϕ
)
=
cos
ϕ
,
sin
(
360
o
+
ϕ
)
=
sin
ϕ
,
tg
(
180
o
+
ϕ
)
=
tg
ϕ
.
{\displaystyle \cos(360^{o}+\phi )=\cos \phi ,\;\sin(360^{o}+\phi )=\sin \phi ,\;\operatorname {tg} (180^{o}+\phi )=\operatorname {tg} \phi .}
Период синусне и косинусне функције може се наћи из формуле:
T
=
2
π
ω
{\displaystyle T={\frac {2\pi }{\omega }}}
Тако је период функције
sin
2
α
{\displaystyle \sin {2\alpha }}
T
=
2
π
2
{\displaystyle T={\frac {2\pi }{2}}}
π
{\displaystyle \pi }
Функције углове већих од 360 степени претходним формулама се своде на функције мањих углова, а затим даље, ако је потребно, на први квадрант, на начин видљив у следећој табели:
β
{\displaystyle \beta \,}
π
2
+
α
{\displaystyle {\frac {\pi }{2}}+\alpha }
π
+
α
{\displaystyle \pi +\alpha \,}
3
π
2
+
α
{\displaystyle {\frac {3\,\pi }{2}}+\alpha }
π
2
−
α
{\displaystyle {\frac {\pi }{2}}-\alpha }
π
−
α
{\displaystyle \pi -\alpha \,}
3
π
2
−
α
{\displaystyle {\frac {3\,\pi }{2}}-\alpha }
2
π
−
α
{\displaystyle 2\,\pi -\alpha }
sin
β
{\displaystyle \sin \beta \,}
cos
α
{\displaystyle \cos \alpha \,}
−
sin
α
{\displaystyle -\sin \alpha \,}
−
cos
α
{\displaystyle -\cos \alpha \,}
cos
α
{\displaystyle \cos \alpha \,}
sin
α
{\displaystyle \sin \alpha \,}
−
cos
α
{\displaystyle -\cos \alpha \,}
−
sin
α
{\displaystyle -\sin \alpha \,}
cos
β
{\displaystyle \cos \beta \,}
−
sin
α
{\displaystyle -\sin \alpha \,}
−
cos
α
{\displaystyle -\cos \alpha \,}
sin
α
{\displaystyle \sin \alpha \,}
sin
α
{\displaystyle \sin \alpha \,}
−
cos
α
{\displaystyle -\cos \alpha \,}
−
sin
α
{\displaystyle -\sin \alpha \,}
cos
α
{\displaystyle \cos \alpha \,}
tg
β
{\displaystyle \operatorname {tg} \,\beta }
−
ctg
α
{\displaystyle -\operatorname {ctg} \,\alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
−
ctg
α
{\displaystyle -\operatorname {ctg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
−
tg
α
{\displaystyle -\operatorname {tg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
ctg
β
{\displaystyle \operatorname {ctg} \,\beta }
−
tg
α
{\displaystyle -\operatorname {tg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
−
tg
α
{\displaystyle -\operatorname {tg} \,\alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
−
ctg
α
{\displaystyle -\operatorname {ctg} \,\alpha }
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
У општем случају то се може записати овако:
f
(
n
π
+
α
)
=
±
f
(
α
)
{\displaystyle f(n\pi +\alpha )=\pm f(\alpha )}
f
(
n
π
−
α
)
=
±
f
(
α
)
{\displaystyle f(n\pi -\alpha )=\pm f(\alpha )}
f
(
(
2
n
+
1
)
π
2
+
α
)
=
±
g
(
α
)
{\displaystyle f\left({\frac {(2n+1)\pi }{2}}+\alpha \right)=\pm g(\alpha )}
f
(
(
2
n
+
1
)
π
2
−
α
)
=
±
g
(
α
)
{\displaystyle f\left({\frac {(2n+1)\pi }{2}}-\alpha \right)=\pm g(\alpha )}
Притом је f — произвољна тригонометријска функција, g — одговарајућа јој функција (косинус за синуса, синус за косинус и аналогно за остале функције), а n — цео број .
Вредности тригонометријских функција приказане на тригонометријској кружници За неке од углова из првог квадранта се функције лакше израчунавају:
Најчешће вредности тригонометријских функција
ϕ
{\displaystyle \phi \,}
0°
30°
45°
60°
90°
sin
ϕ
{\displaystyle \sin \phi \,}
0
1
2
{\displaystyle {\frac {1}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
1
cos
ϕ
{\displaystyle \cos \phi \,}
1
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
Рашчлањивање није успело (SVG (MathML се може укључити преко плугина за прегледач): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/sr.wikipedia.org/v1/":): {\displaystyle \frac{1}{2}}
0
tg
ϕ
{\displaystyle \operatorname {tg} \phi }
0
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
1
3
{\displaystyle {\sqrt {3}}}
±
∞
{\displaystyle \pm \infty }
Један од начина израчунавања ових вредности је приказан у прегледу основних углова . Из табеле се види да су већ код „основних“ углова тригонометријске функције ирационални бројеви и да би слични изрази за друге углове могли бити још сложенији. Једноставнији од тих сложенијих израза био би, на пример
sin
15
o
=
3
−
1
2
2
,
{\displaystyle \sin 15^{o}={\frac {{\sqrt {3}}-1}{2{\sqrt {2}}}},}
тригонометријске таблице , на 5 до 10 децимала , a у последње време користи се скоро искључиво рачунар или калкулатор .
Вредности тригонометријских функција неких углова које се нешто дужим путем израчунавају дати су у следећој табели:
α
{\displaystyle \alpha \,}
π
12
=
15
∘
{\displaystyle {\frac {\pi }{12}}=15^{\circ }}
π
10
=
18
∘
{\displaystyle {\frac {\pi }{10}}=18^{\circ }}
π
8
=
22.5
∘
{\displaystyle {\frac {\pi }{8}}=22.5^{\circ }}
π
5
=
36
∘
{\displaystyle {\frac {\pi }{5}}=36^{\circ }}
3
π
10
=
54
∘
{\displaystyle {\frac {3\,\pi }{10}}=54^{\circ }}
3
π
8
=
67.5
∘
{\displaystyle {\frac {3\,\pi }{8}}=67.5^{\circ }}
2
π
5
=
72
∘
{\displaystyle {\frac {2\,\pi }{5}}=72^{\circ }}
sin
α
{\displaystyle \sin \alpha \,}
3
−
1
2
2
{\displaystyle {\frac {{\sqrt {3}}-1}{2\,{\sqrt {2}}}}}
5
−
1
4
{\displaystyle {\frac {{\sqrt {5}}-1}{4}}}
2
−
2
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}
5
−
5
2
2
{\displaystyle {\frac {\sqrt {5-{\sqrt {5}}}}{2\,{\sqrt {2}}}}}
5
+
1
4
{\displaystyle {\frac {{\sqrt {5}}+1}{4}}}
2
+
2
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}
5
+
5
2
2
{\displaystyle {\frac {\sqrt {5+{\sqrt {5}}}}{2\,{\sqrt {2}}}}}
cos
α
{\displaystyle \cos \alpha \,}
3
+
1
2
2
{\displaystyle {\frac {{\sqrt {3}}+1}{2\,{\sqrt {2}}}}}
5
+
5
2
2
{\displaystyle {\frac {\sqrt {5+{\sqrt {5}}}}{2\,{\sqrt {2}}}}}
2
+
2
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}
5
+
1
4
{\displaystyle {\frac {{\sqrt {5}}+1}{4}}}
5
−
5
2
2
{\displaystyle {\frac {\sqrt {5-{\sqrt {5}}}}{2\,{\sqrt {2}}}}}
2
−
2
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}
5
−
1
4
{\displaystyle {\frac {{\sqrt {5}}-1}{4}}}
tg
α
{\displaystyle \operatorname {tg} \,\alpha }
2
−
3
{\displaystyle 2-{\sqrt {3}}}
1
−
2
5
{\displaystyle {\sqrt {1-{\frac {2}{\sqrt {5}}}}}}
2
−
1
2
+
1
{\displaystyle {\sqrt {\frac {{\sqrt {2}}-1}{{\sqrt {2}}+1}}}}
5
−
2
5
{\displaystyle {\sqrt {5-2\,{\sqrt {5}}}}}
1
+
2
5
{\displaystyle {\sqrt {1+{\frac {2}{\sqrt {5}}}}}}
2
+
1
2
−
1
{\displaystyle {\sqrt {\frac {{\sqrt {2}}+1}{{\sqrt {2}}-1}}}}
5
+
2
5
{\displaystyle {\sqrt {5+2\,{\sqrt {5}}}}}
ctg
α
{\displaystyle \operatorname {ctg} \,\alpha }
2
+
3
{\displaystyle 2+{\sqrt {3}}}
5
+
2
5
{\displaystyle {\sqrt {5+2\,{\sqrt {5}}}}}
2
+
1
2
−
1
{\displaystyle {\sqrt {\frac {{\sqrt {2}}+1}{{\sqrt {2}}-1}}}}
1
+
2
5
{\displaystyle {\sqrt {1+{\frac {2}{\sqrt {5}}}}}}
5
−
2
5
{\displaystyle {\sqrt {5-2\,{\sqrt {5}}}}}
2
−
1
2
+
1
{\displaystyle {\sqrt {\frac {{\sqrt {2}}-1}{{\sqrt {2}}+1}}}}
1
−
2
5
{\displaystyle {\sqrt {1-{\frac {2}{\sqrt {5}}}}}}
Када тачка D једном обиђе кружницу пређе пут 2π односно направи 360°. Лук дужине π одговара углу 180° - испружени угао, π/2 је 90° - прави угао, π/3 је 60°, π/4 је 45°, π/6 је 30°, и уопште лук дужине x радијана одговара углу 360x /2π степени. За један радијан , х = 1, добија се угао 57,2957795... степени , тј. у степенима, минутима и секундама 57°17'44,8". Један степен има 60 минута, а једна минута има 60 секунди. Изрази минуте и секунде потичу од латинских речи: partes minutae primae и partes minutae secundae , тј. први мали делови и други мали делови. Математички текстови за јединицу угла подразумевају радијан.
Тригонометријске функције се, такође, могу представљати (бесконачним) редовима :
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
.
.
.
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+...=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
.
.
.
==
∑
n
=
0
∞
(
−
1
)
n
x
2
n
(
2
n
)
!
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+...==\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}
Ови редови се могу употребити и за дефинисање тригонометријских функција комплексног броја z, и хиперболичких функција .
Имајући у виду једнакости
tg
x
=
sin
x
cos
x
,
{\displaystyle \operatorname {tg} \,x={\frac {\sin x}{\cos x}},}
ctg
x
=
cos
x
sin
x
,
{\displaystyle \operatorname {ctg} \,x={\frac {\cos x}{\sin x}},}
sec
x
=
1
cos
x
{\displaystyle \sec x={\frac {1}{\cos x}}}
cosec
x
=
1
sin
x
,
{\displaystyle \operatorname {cosec} \,x={\frac {1}{\sin x}},}
Тејлоров ред се могу разложити следеће функције:
tg
x
=
x
+
1
3
x
3
+
2
15
x
5
+
17
315
x
7
+
62
2835
x
9
+
⋯
=
∑
n
=
1
∞
2
2
n
(
2
2
n
−
1
)
|
B
2
n
|
(
2
n
)
!
x
2
n
−
1
(
−
π
2
<
x
<
π
2
)
,
{\displaystyle {\operatorname {tg} \,x=x+{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}+{\frac {17}{315}}\,x^{7}+{\frac {62}{2835}}\,x^{9}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}}x^{2n-1}\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}
ctg
x
=
1
x
−
x
3
−
x
3
45
−
2
x
5
945
−
x
7
4725
−
⋯
=
1
x
+
∑
n
=
1
∞
(
−
1
)
n
2
2
n
|
B
2
n
|
(
2
n
)
!
x
2
n
−
1
(
−
π
<
x
<
π
)
,
{\displaystyle {\operatorname {ctg} \,x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-{\frac {x^{7}}{4725}}-\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {(-1)^{n}2^{2n}|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),}}
sec
x
=
1
+
1
2
x
2
+
5
24
x
4
+
61
720
x
6
+
277
8064
x
8
+
⋯
=
1
+
∑
n
=
1
∞
E
n
(
2
n
)
!
x
2
n
,
(
−
π
2
<
x
<
π
2
)
,
{\displaystyle {\sec x=1+{\frac {1}{2}}\,x^{2}+{\frac {5}{24}}\,x^{4}+{\frac {61}{720}}\,x^{6}+{\frac {277}{8064}}\,x^{8}+\cdots =1+\sum _{n=1}^{\infty }{\frac {E_{n}}{(2n)!}}\,x^{2n},\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}
csc
x
=
1
x
+
1
6
x
+
7
360
x
3
+
31
15120
x
5
+
127
604800
x
7
+
⋯
=
1
x
+
∑
n
=
1
∞
2
(
2
2
n
−
1
−
1
)
B
n
(
2
n
)
!
x
2
n
−
1
(
−
π
<
x
<
π
)
,
{\displaystyle {\csc x={\frac {1}{x}}+{\frac {1}{6}}\,x+{\frac {7}{360}}\,x^{3}+{\frac {31}{15120}}\,x^{5}+{\frac {127}{604800}}\,x^{7}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2\,(2^{2n-1}-1)B_{n}}{(2n)!}}x^{2n-1}\quad \left(-\pi <x<\pi \right),}}
Тригонометријске функције се могу графички представити. На следећим сликама су приказани њихови графици:
Графици тригонометријских функција: синуса , косинуса , тангенса , секанса , косеканса , котангенса Косинус и секанс су парне функције , док су преостале четири непарне функције :
sin
(
−
α
)
=
−
sin
α
,
{\displaystyle \sin \left(-\alpha \right)=-\sin \alpha \,,}
cos
(
−
α
)
=
cos
α
,
{\displaystyle \cos \left(-\alpha \right)=\cos \alpha \,,}
t
g
(
−
α
)
=
−
t
g
α
,
{\displaystyle \mathop {\mathrm {tg} } \,\left(-\alpha \right)=-\mathop {\mathrm {tg} } \,\alpha \,,}
c
t
g
(
−
α
)
=
−
c
t
g
α
,
{\displaystyle \mathop {\mathrm {ctg} } \,\left(-\alpha \right)=-\mathop {\mathrm {ctg} } \,\alpha \,,}
sec
(
−
α
)
=
sec
α
,
{\displaystyle \sec \left(-\alpha \right)=\sec \alpha \,,}
c
o
s
e
c
(
−
α
)
=
−
c
o
s
e
c
α
.
{\displaystyle \mathop {\mathrm {cosec} } \,\left(-\alpha \right)=-\mathop {\mathrm {cosec} } \,\alpha \,.}
Сл.4. Тетива је краћа од лука На слици (4) лево видимо тетиву
D
A
H
¯
{\displaystyle {\overline {DAH}}}
лука
D
B
H
^
.
{\displaystyle {\widehat {DBH}}.}
Тетива је најкраће растојање између две тачке на кружници . Зато је полутетива
D
A
¯
{\displaystyle {\overline {DA}}}
D
B
^
.
{\displaystyle {\widehat {DB}}.}
правоугли . Прави угао је у темену А, катета ОА износи
cos
ϕ
{\displaystyle \cos \phi }
sin
ϕ
{\displaystyle \sin \phi }
хипотенуза је дужине један. Када је угао у радијанима и
0
<
ϕ
<
π
2
,
{\displaystyle 0<\phi <{\frac {\pi }{2}},}
Теорема 1
lim
ϕ
→
0
sin
ϕ
=
0
,
lim
ϕ
→
0
cos
ϕ
=
1.
{\displaystyle \lim _{\phi \to 0}\sin \phi =0,\;\lim _{\phi \to 0}\cos \phi =1.}
Доказ : Следи из
0
<
sin
ϕ
<
D
B
^
=
ϕ
{\displaystyle 0<\sin \phi <{\widehat {DB}}=\phi }
0
<
1
−
cos
ϕ
<
A
B
¯
<
D
B
¯
<
D
B
^
=
ϕ
.
{\displaystyle 0<1-\cos \phi <{\overline {AB}}<{\overline {DB}}<{\widehat {DB}}=\phi .}
Када угао тежи нули преко позитивних вредности, синус је тада позитиван, а негативан је када угао тежи нули преко негативних вредности. Напротив, косинус је у оба случаја позитиван. Из тога произилазе лимеси за котангенс :
lim
x
→
+
0
ctg
x
=
+
∞
,
lim
x
→
−
0
ctg
x
=
−
∞
.
{\displaystyle \lim _{x\to +0}\operatorname {ctg} x=+\infty ,\;\lim _{x\to -0}\operatorname {ctg} x=-\infty .}
комплементним углом добићете одговарајуће лимесе за тангенс .
Сл.5. Тригонометријски круг Теорема 2
lim
x
→
0
sin
x
x
=
1.
{\displaystyle \lim _{x\to \ 0}{\frac {\sin x}{x}}=1.}
Доказ
На слици (5) десно, површина правоуглог троугла OAD мања је од површине кружног исечка OBD, а ова опет мања од површине правоуглог троугла OBE. Назовимо са х угао BOE. Отуда
sin
x
cos
x
2
<
x
2
<
tg
x
2
.
{\displaystyle {\frac {\sin x\cos x}{2}}<{\frac {x}{2}}<{\frac {\operatorname {tg} x}{2}}.}
sin
x
2
,
{\displaystyle {\frac {\sin x}{2}},}
cos
x
<
x
sin
x
<
1
cos
x
,
{\displaystyle \cos x<{\frac {x}{\sin x}}<{\frac {1}{\cos x}},}
1
cos
x
>
sin
x
x
>
cos
x
.
{\displaystyle {\frac {1}{\cos x}}>{\frac {\sin x}{x}}>\cos x.}
x
→
0
{\displaystyle x\to 0}
cos
x
→
1
,
1
cos
x
→
1
,
{\displaystyle \cos x\to 1,\;{\frac {1}{\cos x}}\to 1,}
sin
x
x
→
1.
{\displaystyle {\frac {\sin x}{x}}\to 1.}
Извод функције f(x) по дефиницији је гранична вредност :
f
′
(
x
)
=
lim
Δ
x
→
0
Δ
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
.
{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {\Delta f(x)}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}.}
Теорема 3
(а)
(
sin
x
)
′
=
cos
x
,
{\displaystyle (\sin x)'=\cos x,\,}
(б)
(
cos
x
)
′
=
−
sin
x
,
{\displaystyle (\cos x)'=-\sin x,\,}
(в)
(
tg
x
)
′
=
sec
2
x
.
{\displaystyle (\operatorname {tg} x)'=\sec ^{2}x.\,}
(г)
(
ctg
x
)
′
=
−
csc
2
x
.
{\displaystyle (\operatorname {ctg} x)'=-\csc ^{2}x.\,}
Доказ
(а)
Δ
sin
x
=
sin
(
x
+
Δ
x
)
−
sin
x
=
2
cos
(
x
+
Δ
x
2
)
sin
Δ
x
2
,
{\displaystyle \Delta \sin x=\sin(x+\Delta x)-\sin x=2\cos \left(x+{\frac {\Delta x}{2}}\right)\sin {\frac {\Delta x}{2}},}
Δ
sin
x
Δ
x
=
cos
(
x
+
Δ
x
2
)
Δ
x
2
→
cos
x
,
{\displaystyle {\frac {\Delta \sin x}{\Delta x}}={\frac {\cos(x+{\frac {\Delta x}{2}})}{\frac {\Delta x}{2}}}\rightarrow \cos x,}
Δ
x
→
0
{\displaystyle \Delta x\rightarrow 0}
(б) Због
cos
x
=
sin
(
π
2
−
x
)
,
{\displaystyle \cos x=\sin({\frac {\pi }{2}}-x),}
(
cos
x
)
′
=
cos
(
π
2
−
x
)
⋅
(
π
2
−
x
)
′
=
−
cos
(
π
2
−
x
)
=
−
sin
x
.
{\displaystyle (\cos x)'=\cos({\frac {\pi }{2}}-x)\cdot ({\frac {\pi }{2}}-x)'=-\cos({\frac {\pi }{2}}-x)=-\sin x.}
(в) Извод количника
(
tg
x
)
′
=
(
sin
x
cos
x
)
′
=
{\displaystyle (\operatorname {tg} x)'=\left({\frac {\sin x}{\cos x}}\right)'=}
=
sin
′
x
cos
x
−
cos
′
x
sin
x
cos
2
x
=
cos
2
x
+
sin
2
x
cos
2
x
=
1
cos
2
x
=
sec
2
x
.
{\displaystyle ={\frac {\sin 'x\cos x-\cos 'x\sin x}{\cos ^{2}x}}={\frac {\cos ^{2}x+\sin ^{2}x}{\cos ^{2}x}}={\frac {1}{\cos ^{2}x}}=\sec ^{2}x.}
(г) Извод количника
(
ctg
x
)
′
=
(
cos
x
sin
x
)
′
=
{\displaystyle (\operatorname {ctg} x)'=\left({\frac {\cos x}{\sin x}}\right)'=}
=
cos
′
x
sin
x
−
sin
′
x
cos
x
sin
2
x
=
−
sin
2
x
−
cos
2
x
sin
2
x
=
−
1
sin
2
x
=
−
csc
2
x
.
{\displaystyle ={\frac {\cos 'x\sin x-\sin 'x\cos x}{\sin ^{2}x}}={\frac {-\sin ^{2}x-\cos ^{2}x}{\sin ^{2}x}}=-{\frac {1}{\sin ^{2}x}}=-\csc ^{2}x.}
Интеграли неких тригонометријских функција приказани су овде:
f
(
x
)
{\displaystyle \ \ \ \ f(x)}
f
′
(
x
)
{\displaystyle \ \ \ \ f'(x)}
∫
f
(
x
)
d
x
{\displaystyle \int f(x)\,dx}
sin
x
{\displaystyle \,\ \sin x}
cos
x
{\displaystyle \,\ \cos x}
−
cos
x
+
C
{\displaystyle \,\ -\cos x+C}
cos
x
{\displaystyle \,\ \cos x}
−
sin
x
{\displaystyle \,\ -\sin x}
sin
x
+
C
{\displaystyle \,\ \sin x+C}
tan
x
{\displaystyle \,\ \tan x}
sec
2
x
=
1
+
tan
2
x
{\displaystyle \,\ \sec ^{2}x=1+\tan ^{2}x}
−
ln
|
cos
x
|
+
C
{\displaystyle -\ln \left|\cos x\right|+C}
cot
x
{\displaystyle \,\ \cot x}
−
csc
2
x
=
−
(
1
+
cot
2
x
)
{\displaystyle \,\ -\csc ^{2}x=-(1+\cot ^{2}x)}
ln
|
sin
x
|
+
C
{\displaystyle \ln \left|\sin x\right|+C}
sec
x
{\displaystyle \,\ \sec x}
sec
x
tan
x
{\displaystyle \,\ \sec x\tan x}
ln
|
sec
x
+
tan
x
|
+
C
{\displaystyle \ln \left|\sec x+\tan x\right|+C}
csc
x
{\displaystyle \,\ \csc x}
−
csc
x
cot
x
{\displaystyle \,\ -\csc x\cot x}
−
ln
|
csc
x
+
cot
x
|
+
C
{\displaystyle \ -\ln \left|\csc x+\cot x\right|+C}
Преглед скоро свих особина тригонометријских функција које се тичу решавања троуглова дат је у прилогу: равнинска тригонометрија .
У посебном прилогу могу се пронаћи докази за адиционе формуле , где спадају и формуле за двоструке углове , затим половине углова , те представљање збира и разлике тригонометријских функција помоћу производа и обратно, и изражавање осталих тригонометријских функција помоћу тангенса половине угла.
Такође, у посебном прилогу се налазе тригонометријске једначине .
[ уреди | уреди извор ] Тригонометријске функције косинус и синус могу се представити као решења диференцијалне једначине :
d
2
d
φ
2
R
(
φ
)
=
−
R
(
φ
)
,
{\displaystyle {\frac {d^{2}}{d\varphi ^{2}}}R(\varphi )=-R(\varphi ),}
са почетним условом
cos
(
0
)
=
sin
′
(
0
)
=
1
{\displaystyle \cos(0)=\sin '(0)=1}
cos
″
x
=
−
cos
x
,
{\displaystyle \ \cos ''x=-\cos x,}
sin
″
x
=
−
sin
x
.
{\displaystyle \ \sin ''x=-\sin x.}
[ уреди | уреди извор ] Функције косинус и синус се могу одредити као непрекидна решења система функционалних једначина :
{
f
(
x
+
y
)
=
f
(
x
)
f
(
y
)
−
g
(
x
)
g
(
y
)
g
(
x
+
y
)
=
g
(
x
)
f
(
y
)
+
f
(
x
)
g
(
y
)
{\displaystyle \left\{{\begin{array}{rcl}f(x+y)&=&f(x)f(y)-g(x)g(y)\\g(x+y)&=&g(x)f(y)+f(x)g(y)\end{array}}\right.}
Инверзне тригонометријске функције су arcsin x (аркус синус икс), arccos x (аркус косинус ), arctg x (аркус тангенс ), arcctg x (аркус котангенс ). Оне су инверзне тригонометријским функцијама sin x (синус икс), cos x (косинус ), tg x (тангенс ), ctg x (котангенс ). Префикс аркус потиче од латинске речи arcus - лук, угао. Називају се још и циклометријским функцијама.
za
−
π
2
≤
y
≤
π
2
,
y
=
arcsin
x
ako
x
=
sin
y
;
za
0
≤
y
≤
π
,
y
=
arccos
x
ako
x
=
cos
y
;
za
−
π
2
<
y
<
π
2
,
y
=
arctan
x
ako
x
=
tan
y
;
za
−
π
2
≤
y
≤
π
2
,
y
≠
0
,
y
=
arccsc
x
ako
x
=
csc
y
;
za
0
≤
y
≤
π
,
y
≠
π
2
,
y
=
arcsec
x
ako
x
=
sec
y
;
za
0
<
y
<
π
,
y
=
arccot
x
ako
x
=
cot
y
.
{\displaystyle {\begin{matrix}{\mbox{za}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},&y=\arcsin x&{\mbox{ako}}&x=\sin y\,;\\\\{\mbox{za}}&0\leq y\leq \pi ,&y=\arccos x&{\mbox{ako}}&x=\cos y\,;\\\\{\mbox{za}}&-{\frac {\pi }{2}}<y<{\frac {\pi }{2}},&y=\arctan x&{\mbox{ako}}&x=\tan y\,;\\\\{\mbox{za}}&-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}},y\neq 0,&y=\operatorname {arccsc} x&{\mbox{ako}}&x=\csc y\,;\\\\{\mbox{za}}&0\leq y\leq \pi ,y\neq {\frac {\pi }{2}},&y=\operatorname {arcsec} x&{\mbox{ako}}&x=\sec y\,;\\\\{\mbox{za}}&0<y<\pi ,&y=\operatorname {arccot} x&{\mbox{ako}}&x=\cot y\,.\end{matrix}}}
Примена тригонометрије и тригонометријских функција у физици је јако велика.
Тако се на пример прилично користе у анализи простирања таласа, описивању хармонијских осцилација као периодичног кретања, представљања наизменичне струје итд.
Тригонометријске и хиперболичке функције
Групе Остало