Глобус

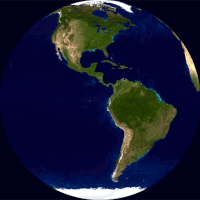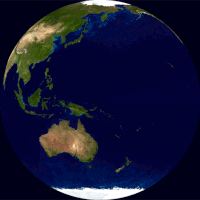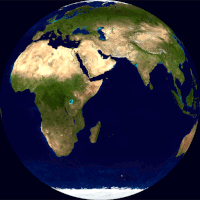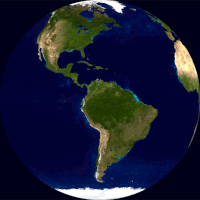
Глобус (лат. globus — „лопта”) је умањени лоптасти приказ Земље, планета или небеске сфере са уцртаним картографским приказом дате површине. Однос и геометријска подударност са стварним приказима је најсличнија од свих могућих интерпретација (мапа и др). Према типу глобуси се могу поделити на географске и астрономске.[1] У настави географије, сферни приказ Земље је један од основних учила.
Глобус приказује детаље своје теме. Земаљски глобус приказује копнене масе[2][3][4][5][6] и водена тела.[7][8][9] Он може да прикаже нације и веће градове и мрежу линија географске ширине и дужине.[10][11] Неки имају подигнути рељеф да би приказали планине и друге велике рељефне облике. Небески глобус приказује значајне звезде, а може да приказује и положаје других истакнутих астрономских објеката. Обично ће такође поделити небеску сферу на сазвежђа.
Земаљски и планетарни
[уреди | уреди извор]
Равне карте се креирају коришћењем пројекције карте која неизбежно уноси све већу количину изобличења што је већа површина коју мапа приказује.[12][13][14][15][16] Глобус је једини приказ Земље који не искривљује ни облик ни величину великих обележја – копнених маса, водених површина итд.
Обим Земље је прилично близу 40 милиона метара.[17][18] Многи глобуси су направљени са обимом од једног метра, тако да су модели Земље у размери 1:40 милиона. У империјалним јединицама, многи глобуси се праве са пречником од једне стопе (око 30 cm), што даје обим од 3,14 стопа (око 96 cm) и размеру од 1:42 милиона. Глобуси се такође праве у многим другим величинама.
Неки глобуси имају површинску текстуру која показује топографију или батиметрију. У њима су узвишења и депресије намерно преувеличане, јер би иначе биле једва видљиве. На пример, један произвођач производи тродимензионални издигнути рељефни глобус пречника 25 in (64 cm) (еквивалентно обиму од 200 cm, или приближно скале од 1:20 милиона) који приказује највише планине преко 1 in (2,5 cm), што је око 57 пута више од тачне скале Монт Евереста.[19][20]
Историја
[уреди | уреди извор]Први глобуси појавили су се још у старом веку, одмах по сазнању да је Земља округла. Првим творцем сматра се Кратес са острва Малос, који је у II веку пре нове ере израдио сферни модел планете.[21] Клаудије Птолемеј је у свом делу „Географија“, дао упутства за израду глобуса. Током XIII века у арапском свету је направљеном неколико модела Земље, само два у сачувана до данас. Мартин Бехајм је 1492. године конструисао први глобус у средњем веку, и то пре открића Новог света.
Особине
[уреди | уреди извор]Пресликавање Земљине површине на глобус врши се по правилима централне пројекције. Наиме, замисле се две идентичне лопте са заједничих центром, од којих је Земља већа, а узета сфера мања. Затим, се тачке пројектују замишљеним зрацима који се састају у заједничком средишту. Тиме се пројекције површина са Земље налазе на глобусу у тачкама пресецања. Размер глобуса је једнак у свакој тачки. Углови са модела су једнаки истоветним на Земљиној лопти, па се то назива конформност. Такође и однос површина је у размери.
Главна својства сваког глобуса су: очување сличности фигуре, конформност углова и еквивалентност површина и линија. На основу ових показатеља глобус је навернији и најприближнији приказ Земљине лопте. На лопту малог пречника повлаче се географске координате (упоредници и подневци), осовине које повезују северни и јужни пол нагну су за 23 степена и 27 минута и унесе се географски садржај. Израђују се модели који имају приближан облик Земље да би се избегле све деформације. На њему не постоје деформације дужина у било ком правцу, као ни углова без обзира на правац пружања кракова. Због свега тога глобус је веран приказ Земљине површине.[22]
Размер глобуса
[уреди | уреди извор]Размера је по правилу мала. Најчешће се израђују са пречником од 50 до 60cm. То је у ствари размера од 1:25 000 000 до 1:21 000 000. На тој размери разлика између Земљиних полуоса не прелази дужину од 1 mm. То је занемарљива разлика што омогућава да се глобуси израђују као лопте, а не као елипсоиди. На међународној изложби у Паризу 1889. године изложен је модел пречника 12,5 m и тежак око десет тона у размери 1:1.000.000. Један од најмањих глобуса потиче из 1507. године и познат је као Јагеловски глобус из Кракова. Његов пречник је 7,3 cm.[22]
Подела
[уреди | уреди извор]Глобуси се могу поделити на више типова.[1]
- географске (општи, тематски и индукциони)
- астрономске (звездани, планетарни и месечеви)
Галерија
[уреди | уреди извор]-
Небески глобус
-
Глобуси
-
Бехајмов глобус
-
Реплика старог француског глобуса
Види још
[уреди | уреди извор]Референце
[уреди | уреди извор]- ^ а б Мастило, Наталија (2005). Речник савремене српске географске терминологије. Београд: Географски факултет Универзитета у Београду. стр. 58.
- ^ „Landmass”. Cambridge Dictionary. Cambridge.org Dictionary. Приступљено 17. 1. 2023.
- ^ „Landmass”. Merriam-Webster. Merriam-Webster.com Dictionary. Приступљено 17. 1. 2023.
- ^ Cook, Peter J.; Carleton, Chris M., ур. (9. 11. 2000). Continental Shelf Limits: The Scientific and Legal Interface. Oxford University Press. стр. 298. ISBN 9780197561218. doi:10.1093/oso/9780195117820.001.0001 — преко Google Books.
- ^ Nijman, Jan; Muller, Peter O.; de Blij, H.J. (2017). „Introduction”. Regions: Geography: Realms, Regions, and Concepts (17th изд.). Wiley. стр. 11. ISBN 978-1-119-30189-9.
- ^ „Landmass”. Dictionary.com. Dictionary.com, LLC. Приступљено 25. 7. 2020.
- ^ Langbein, W.B.; Iseri, Kathleen T. (1995). „Hydrologic Definitions: Stream”. Manual of Hydrology: Part 1. General Surface-Water Techniques (Water Supply Paper 1541-A). Reston, VA: USGS..
- ^ „What causes high tide and low tide? Why are there two tides each day?”. HowStuffWorks (на језику: енглески). 21. 5. 2009. Приступљено 10. 12. 2017.
- ^ „European Environment Agency's home page — European Environment Agency”. www.eea.europa.eu (на језику: енглески). Приступљено 2022-11-03.
- ^ Chang, Kang-tsung (2016). Introduction to Geographic Information Systems (9th изд.). McGraw-Hill. стр. 24. ISBN 978-1-259-92964-9.
- ^ Taylor, Chuck. „Locating a Point On the Earth”. Архивирано из оригинала 3. 3. 2016. г. Приступљено 4. 3. 2014.
- ^ Lambert, Johann; Tobler, Waldo (2011). Notes and comments on the composition of terrestrial and celestial maps. Redlands, CA: ESRI Press. ISBN 978-1-58948-281-4.
- ^ Richardus, Peter; Adler, Ron (1972). map projections. New York, NY: American Elsevier Publishing Company, inc. ISBN 0-444-10362-7.
- ^ Robinson, Arthur; Randall, Sale; Morrison, Joel; Muehrcke, Phillip (1985). Elements of Cartography (fifth изд.). ISBN 0-471-09877-9.
- ^ Snyder, J.P.; Voxland, P.M. (1989). „An album of map projections”. Album of Map Projections (PDF). U.S. Geological Survey Professional Paper. 1453. United States Government Printing Office. doi:10.3133/pp1453. Приступљено 8. 3. 2022.
- ^ Ghaderpour, E. (2016). „Some equal-area, conformal and conventional map projections: a tutorial review”. Journal of Applied Geodesy. 10 (3): 197—209. Bibcode:2016JAGeo..10..197G. S2CID 124618009. arXiv:1412.7690
 . doi:10.1515/jag-2015-0033.
. doi:10.1515/jag-2015-0033.
- ^ The Earth’s circumference is 40 million m because the metre was originally defined to be one 10-millionth of the distance between the poles and the equator.
- ^ Arc length#Arcs of great circles on the Earth
- ^ MapScaping på Twitter: "3D topographic globe at Stanford's Branner Library."
- ^ The GEO One 25" Extreme Raised Relief Classroom Floor Globe
- ^ Љешевић, Милутин; Живковић, Драгица (2001). Картографија. Београд: Географски факултет Универзитета у Београду. стр. 25—34.
- ^ а б Ћурчић, Слободан; Ристановић, Бранко (2010). Картографија. Нови Сад: Природно-математички факултет, Департман за географију, туризам и хотелијерство. стр. 138—139.
Литература
[уреди | уреди извор]- Мастило, Н. (2005): Речник савремене српске географске терминологије, Географски факултет, Београд; ISBN 978-86-82657-55-2
- Љешевић, А. и Живковић, Д. (2001): Картографија, Географски факултет, Београд; ISBN 978-86-83501-06-9
- Oliver, Bernard M. (1972). „The Shape of the Analemma”. Sky and Telescope. 44: 20. Bibcode:1972S&T....44...20O.
- Kittler, Richard; Darula, Stan (2004). „Analemma, the Ancient Sketch of Fictitious Sunpath Geometry—Sun, Time and History of Mathematics”. Architectural Science Review. 47 (2): 141—4. S2CID 122005748. doi:10.1080/00038628.2004.9697037.
- Sidoli, Nathan (2005). „Heron's Dioptra 35 and Analemma Methods: An Astronomical Determination of the Distance between Two Cities”. Centaurus. 47 (3): 236—58. Bibcode:2005Cent...47..236S. doi:10.1111/j.1600-0498.2005.470304.x.
- Semazzi, Fredrick H.M.; Scroggs, Jeffrey S.; Pouliot, George A.; McKee-Burrows, Analemma Leia; Norman, Matthew; Poojary, Vikram; Tsai, Yu-Ming (2005). „On the Accuracy of Semi-Lagrangian Numerical Simulation of Internal Gravity Wave Motion in the Atmosphere”. Journal of the Meteorological Society of Japan. 83 (5): 851—69. doi:10.2151/jmsj.83.851
 .
. - Luckey, P. (1927). „Das Analemma von Ptolemäus” [The analemma by Ptolemy]. Astronomische Nachrichten (на језику: немачки). 230 (2): 17—46. Bibcode:1927AN....230...17L. doi:10.1002/asna.19272300202.
- Id, Yusif (децембар 1969). „An Analemma Construction for Right and Oblique Ascensions”. The Mathematics Teacher. 62 (8): 669—72. JSTOR 27958259. doi:10.5951/MT.62.8.0669.
- Yeow, Teo Shin (2002). The Analemma for Latitudinally-Challenged People (PDF) (BS Thesis). National University of Singapore. Архивирано из оригинала (PDF) 2011-05-17. г. Приступљено 2006-02-05.
- Encyclopædia Britannica (1771), "Geography".
- Darlington, Oscar G. "Gerbert, the Teacher," The American Historical Review (Volume 52, Number 3, 1947): 456–476.
- Kern, Ralf: Wissenschaftliche Instrumente in ihrer Zeit. Vom 15. – 19. Jahrhundert. Verlag der Buchhandlung Walther König 2010, ISBN 978-3-86560-772-0
- Needham, Joseph (1986). Science and Civilization in China: Volume 3. Taipei: Caves Books, Ltd.
- Sivin, Nathan (1995). Science in Ancient China. Brookfield, Vermont: VARIORUM, Ashgate Publishing
- Williams, Henry Smith (2004). A History Of Science. Whitefish, MT: Kessinger Publishing. ISBN 1-4191-0163-3.
- Borchert, Donald M. (2006). In Encyclopedia of Philosophy, 2nd ed. Macmillan Reference. стр. 532—536.
- Dewald, Jonathan (2004). Encyclopedia of the Early Modern World. Charles Scribner's Sons. стр. 148—154.
- Savage-Smith, Emily (1985). A History of Celestial Globes in the Greco-Roman and Islamic Worlds" in Islamicate Celestial Globes: Their History, Construction, and Use. Washington DC: Smithsonian Institution Press.
- Savage-Smith, Emilie (2013). God is beautiful and loves beauty: the object in Islamic art and culture. Yale University Press. стр. 123—155.
- Carey, Moya (2009). „The Gold and Silver Lining: Shams Al-Dīn Muḥammad B. Mu'ayyad Al-'Urḍī's Inlaid Celestial Globe (C. Ad 1288) from the Ilkhanid Observatory at Marāgha”. Iran. 47: 97—108. JSTOR 25651466. S2CID 193493577. doi:10.1080/05786967.2009.11864761 — преко JSTOR.
- „Celestial globe”. National Museums Scotland (на језику: енглески). Приступљено 2020-10-15.
- Savage-Smith, Emilie (1985). Islamicate Celestial Globes: Their History, Construction, and Use. Washington, D.C.: Smithsonian Institution Press.
- „Using the EPSG geodetic parameter dataset, Guidance Note 7-1”. EPSG Geodetic Parameter Dataset. Geomatic Solutions. Архивирано из оригинала 15. 12. 2021. г. Приступљено 15. 12. 2021.
Спољашње везе
[уреди | уреди извор]- Кратка историја картографије: Како су наши преци мапирали свет (ТВ Историја - Званични јутјуб канал)
- ppmglobe – generate strips to glue onto a sphere
- 3D VRML globe
- 3D Java Globe with coastlines, parallels, meridians, etc. Архивирано на сајту Wayback Machine (7. март 2019)
- How to orient a globe in homothetic position to the Earth Архивирано на сајту Wayback Machine (28. јануар 2020)
- Glossary to World Globe Terms Архивирано на сајту Wayback Machine (25. јун 2020)
- Behind the scenes at London's globe-making workshop – a photo essay (August 2017), The Guardian




