Hesov zakon toplote

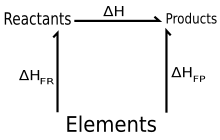
Hesov zakon konstantnog sabiranja toplote, takođe poznat jednostavno kao Hesov zakon, je odnos u fizičkoj hemiji nazvan po Žermenu Hesu, ruskom hemičaru i lekaru rođenom u Švajcarskoj koji ga je objavio 1840. Zakon kaže da se ukupna entalpija promena tokom kompletnog toka hemijske reakcije je nezavisan od redosleda preduzetih koraka. ^[1]^[2]

Hesov zakon se sada shvata kao izraz činjenice da je entalpija hemijskog procesa nezavisna od putanje od početnog do konačnog stanja (tj. entalpija je funkcija stanja). Prema prvom zakonu termodinamike, promena entalpije u sistemu usled reakcije pri konstantnom pritisku jednaka je apsorbovanoj toploti (ili negativu oslobođene toplote), što se može odrediti kalorimetrijom za mnoge reakcije. Vrednosti se obično navode za reakcije sa istim početnim i krajnjim temperaturama i pritiscima (dok je dozvoljeno da uslovi variraju u toku reakcija). Hesov zakon se može koristiti za određivanje ukupne energije potrebne za hemijsku reakciju koja se može podeliti na sintetičke korake koje je pojedinačno lakše okarakterisati. Ovo omogućava kompilaciju standardnih entalpija formiranja, koje se mogu koristiti za predviđanje promene entalpije u kompleksnim sintezama.

Teorija

Hesov zakon kaže da je promena entalpije u hemijskoj reakciji ista bez obzira da li se reakcija odvija u jednom koraku ili u nekoliko koraka, pod uslovom da su početno i konačno stanje reaktanata i proizvoda isti. Entalpija je ekstenzivno svojstvo, što znači da je njena vrednost proporcionalna veličini sistema. ^[3] Zbog toga je promena entalpije proporcionalna broju molova koji učestvuju u datoj reakciji.

Drugim rečima, ako se hemijska promena odvija na nekoliko različitih puteva, ukupna promena entalpije je ista, bez obzira na put kojim se hemijska promena dešava (pod uslovom da su početni i konačni uslovi isti). Ako ovo nije tačno, onda bi se mogao prekršiti prvi zakon termodinamike.

Hesov zakon dozvoljava da se promena entalpije (ΔH) za reakciju izračuna čak i kada se ne može direktno izmeriti. Ovo se postiže izvođenjem osnovnih algebarskih operacija zasnovanih na hemijskim jednačinama reakcija korišćenjem prethodno određenih vrednosti za entalpije formiranja.

Kombinacija hemijskih jednačina dovodi do neto ili ukupne jednačine. Ako su promene entalpije poznate za sve jednačine u nizu, njihov zbir će biti promena entalpije za neto jednačinu. Ako je neto promena entalpije negativna ( $\Delta H_{\text{net}}<0$ ), reakcija je egzotermna i veća je verovatnoća da će biti spontana; pozitivne ΔH vrednosti odgovaraju endotermnim reakcijama. (Entropija takođe igra važnu ulogu u određivanju spontanosti, pošto su neke reakcije sa pozitivnom promenom entalpije ipak spontane zbog povećanja entropije u reakcionom sistemu.)

Upotreba entalpije formiranja

Hesov zakon kaže da su promene entalpije aditivne. Dakle, vrednost od $\Delta H$ za jednu reakciju može se izračunati iz tabelarne entalpije formiranja proizvoda i reaktanata na sledeći način:

\Delta H_{\text{reaction}}^{\ominus }=\sum \nu _{\text{p}}\Delta H_{\mathrm {f} \,({\text{p}})}^{\ominus }-\sum \nu _{\text{r}}\Delta H_{\mathrm {f} \,({\text{r}})}^{\ominus }

Ovde je prvi zbir za sve proizvode p, a drugi za sve reaktante r, $\nu _{\text{p}}$ je stehiometrijski koeficijent proizvoda $\nu _{\text{r}}$ je stehiometrijski koeficijent reaktanta r, $\Delta H_{f(p)}$ je entalpija formiranja proizvoda p, $\Delta H_{f(r)}$ je entalpija formiranja reaktanta r, a gornji indeks ^o označava standardne vrednosti stanja. Ovo se može smatrati zbirom dve (stvarne ili fiktivne) reakcije:

Reaktanti → Elementi (u njihovim standardnim stanjima)

\Delta H_{\text{RE}}^{\ominus }=-\sum \nu _{\text{r}}\Delta H_{\mathrm {f} \,({\text{r}})}^{\ominus }

i Elementi → Proizvodi

\Delta H_{\text{EP}}^{\ominus }=\sum \nu _{\text{p}}\Delta H_{\mathrm {f} \,({\text{p}})}^{\ominus }

Primeri

Daje:
1. C_graphite + O₂ → CO₂(g) ( ΔH = −393.5 kJ/mol) (direct step)
2. C_graphite + 1/2 O₂ → CO(g) (ΔH = −110.5 kJ/mol)
3. CO(g) +1/2 O₂ → CO₂(g) (ΔH = −283.0 kJ/mol)
Reakcija (a) je zbir reakcija (b) i (c), za koje je ukupno ΔH = −393.5 kJ/mol, što je jednako ΔH u (a).
Daje:
- B₂O₃(s) + 3H₂O(g) → 3O₂(g) + B₂H₆(g) (ΔH = 2035 kJ/mol)
- H₂O(l) → H₂O(g) (ΔH = 44 kJ/mol)
- H₂(g) + 1/2 O₂(g) → H₂O(l) (ΔH = −286 kJ/mol)
- 2B(s) + 3H₂(g) → B₂H₆(g) (ΔH = 36 kJ/mol)
Pronađite ΔH_f od:
- 2B(s) + 3/2 O₂(g) → B₂O₃(s)
Nakon množenja jednačina (i njihovih promena entalpije) odgovarajućim faktorima i obrnuta smera kada je potrebno, rezultat je:
- B₂H₆(g) + 3O₂(g) → B₂O₃(s) + 3H₂O(g) (ΔH = 2035 × (−1) = −2035 kJ/mol)
- 3H₂O(g) → 3H₂O(l) (ΔH = 44 × (−3) = −132 kJ/mol)
- 3H₂O(l) → 3H₂(g) + (3/2) O₂(g) (ΔH = −286 × (−3) = 858 kJ/mol)
- 2B(s) + 3H₂(g) → B₂H₆(g) (ΔH = 36 kJ/mol)
Sabirajući ove jednačine i poništavajući zajedničke članove na obe strane, dobijamo:
- 2B(s) + 3/2 O₂(g) → B₂O₃(s) (ΔH = −1273 kJ/mol)

Proširenje na slobodnu energiju i entropiju

Koncepti Hesovog zakona mogu se proširiti i uključiti promene entropije i Gibsove slobodne energije, pošto su to takođe funkcije stanja . Bordvelov termodinamički ciklus je primer takvog proširenja koje koristi prednosti lako merljivih ravnoteža i redoks potencijala za određivanje eksperimentalno nepristupačnih Gibsovih vrednosti slobodne energije. Kombinovanje ΔG^o vrednosti iz Bordvelovih termodinamičkih ciklusa i ΔH^o vrednosti pronađenih sa Hesovim zakonom može biti od pomoći u određivanju vrednosti entropije koje nisu direktno izmerene i stoga ih je potrebno izračunati kroz alternativne puteve.

Za besplatnu energiju:

\Delta G_{\text{reaction}}^{\ominus }=\sum \nu _{\text{p}}\Delta G_{\mathrm {f} \,({\text{p}})}^{\ominus }-\sum \nu _{\text{r}}\Delta G_{\mathrm {f} \,({\text{r}})}^{\ominus }.

Što se tiče entropije, situacija je malo drugačija. Pošto se entropija može meriti kao apsolutna vrednost, a ne u odnosu na one elemenata u njihovim referentnim stanjima (kao kod ΔH^o i ΔG^o), nema potrebe da se koristi entropija formiranja; jednostavno se koriste apsolutne entropije za proizvode i reaktante:

\Delta S_{\text{reaction}}^{\ominus }=\sum \nu _{\text{p}}S_{({\text{p}})}^{\ominus }-\sum \nu _{\text{r}}S_{({\text{r}})}^{\ominus }.

Aplikacije

Hesov zakon je koristan za određivanje entalpija za sledeće: ^[1]

Toplote formiranja nestabilnih intermedijera kao što su CO_(g) and NO_(g).
Promene toplote u faznim prelazima i alotropnim prelazima.
Rešetke energije jonskih supstanci konstruisanjem Born–Haberovih ciklusa ako je poznat afinitet elektrona za formiranje anjona, ili
Elektronski afiniteti korišćenjem Born–Haberovog ciklusa sa teoretskom energijom rešetke.

Vidi još

Reference

^ ^а ^б Mannam Krishnamurthy; Subba Rao Naidu (2012). „7”. Ур.: Lokeswara Gupta. Chemistry for ISEET - Volume 1, Part A (2012 изд.). Hyderabad, India: Varsity Education Management Limited. стр. 244.
^ „Hess' Law - Conservation of Energy”. University of Waterloo. Архивирано из оригинала 9. 1. 2015. г. Приступљено 12. 1. 2014.
^ Engel, Thomas; Reid, Philip (2006). Physical Chemistry. Pearson / Benjamin Cummings. стр. 6. ISBN 0-8053-3842-X. „A variable ... proportional to the size of the system is referred to as an extensive variable.”

Chakrabarty, D.K. (2001). An Introduction to Physical Chemistry. Mumbai: Alpha Science. стр. 34—37. ISBN 1-84265-059-9.

Literatura

Leicester, Henry M. (1951). „Germain Henri Hess and the Foundations of Thermochemistry”. The Journal of Chemical Education. 28 (11): 581–583. Bibcode:1951JChEd..28..581L. doi:10.1021/ed028p581.

Spoljašnje veze

Hess' paper (1840) on which his law is based (na sajtu ChemTeam)
a Hess’ Law experiment Архивирано на сајту Wayback Machine (3. март 2016)

[Aakash1-1] а ^б Mannam Krishnamurthy; Subba Rao Naidu (2012). „7”. Ур.: Lokeswara Gupta. Chemistry for ISEET - Volume 1, Part A (2012 изд.). Hyderabad, India: Varsity Education Management Limited. стр. 244.

[2] „Hess' Law - Conservation of Energy”. University of Waterloo. Архивирано из оригинала 9. 1. 2015. г. Приступљено 12. 1. 2014.

[3] Engel, Thomas; Reid, Philip (2006). Physical Chemistry. Pearson / Benjamin Cummings. стр. 6. ISBN 0-8053-3842-X. „A variable ... proportional to the size of the system is referred to as an extensive variable.”

[1]

[2]

[3]