Молекуларна симетрија

Елементи симетрије формалдехида. C₂ је двострука оса ротације. σ_в анд σ_в' су две нееквивалентне рефлексијске равни.

У хемији, молекуларна_симетрија описује симетрију присутну у молекулима и класификацију ових молекула према њиховој симетрији. Молекуларна симетрија је фундаментални концепт у хемији, јер се може користити за предвиђање или објашњење многих хемијских својстава молекула, као што је да ли има или нема диполни момент, као и његове дозвољене спектроскопске прелазе. Да би се то урадило, потребно је користити теорију група. Ово укључује класификацију стања молекула користећи несводљиве репрезентације из табеле знакова групе симетрије молекула. Симетрија је корисна у проучавању молекуларних орбитала, са применама на Хикелов метод, на теорију поља лиганда и на Вудвард-Хофманова правила. Многи уџбеници на универзитетском нивоу о физичкој хемији, квантној хемији, спектроскопији и неорганској хемији говоре о симетрији. Још један оквир на већем обиму је употреба кристалних система за описивање кристалографске симетрије у расутим материјалима.

Постоји много техника за одређивање симетрије датог молекула, укључујући рендгенску кристалографију и различите облике спектроскопије. Спектроскопска нотација је заснована на разматрањима симетрије.

Концепти симетрије групе тачака

Примери односа између хиралности и симетрије

Ротациона оса (Cн)	Неправилни ротациони елементи (Сн)
	Хирални не Сн	Ахирална раван огледала С1 = σ	Ахирални инверзиони центар С2 = и
C1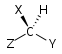
C2

Групе тачака и њихове операције симетрије

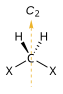Симбол	Операције симетрије
C1	Е
Cс	Е, σ
Cи	Е, и
Cн	Е, Cн
Сн	Е, Сн (ротациона рефлекција)
Cнв	Е, Cн, н*σв
Cнх	Е, Cн, σх
Dн	Е, Cн, н*C2(вертикално)
Dнх	Е, Cн, н*C2(вертикално), σх
Dнд	Е, Cн, н*C2(вертикално), н*σв(до C2 осе)
Тд	Е, 6*σд, 4*C3, 3*С4
Ох	Е, 6*σд, 3*σх, 6*C2, 4*C3, 3*C4, 4*С6

Елементи

Тачкаста групна симетрија молекула је дефинисана присуством или одсуством 5 типова елемента симетрије.

• Оса симетрије: оса око које ротација за ${\tfrac {360^{\circ }}{n}}$ резултира молекулом који се не разликује од оригинала. Ово се такође назива н-струка ротациона оса и скраћено C_н. Примери су C₂ оса у води и C₃ оса у амонијаку. Молекул може имати више од једне осе симетрије; она са највећим н назива се главна оса, и по конвенцији је поравната са з-осом у картезијанском координатном систему.
• Раван симетрије: раван рефлексије кроз коју се генерише идентична копија оригиналног молекула. Ово се такође назива раван огледала и скраћено σ (сигма = грчко „с“, од немачког „Спиегел“ што значи огледало).. Вода има две: једну у равни самог молекула и једну окомито на њега. Раван симетрије паралелна са главном осом назива се вертикална (σ_в), а она нормална на њу хоризонтална (σ_х). Постоји трећи тип равни симетрије: Ако вертикална раван симетрије додатно дели угао између две осе ротације које су управне у односу на главну осу, раван се назива диедарска (σ_д). Раван симетрије се такође може идентификовати по њеној картезијанској оријентацији, нпр. (xз) или (yз).
• Центар симетрије или центар инверзије, скраћено и. Молекул има центар симетрије када, за било који атом у молекулу, идентичан атом постоји дијаметрално насупрот овом центру на једнакој удаљености од њега. Другим речима, молекул има центар симетрије када су тачке (x,y,з) и (−x,−y,−з) идентичне. На пример, ако постоји атом кисеоника у некој тачки (x,y,з), онда постоји атом кисеоника у тачки (−x,−y,−з). У самом центру инверзије може бити или не мора постојати атом. Примери су ксенон тетрафлуорид где је центар инверзије на атому Xе и бензен (C
  6Х
  6) где је центар инверзије у центру прстена.
• Ротационо-рефлексиона оса: оса око које је ротација за ${\tfrac {360^{\circ }}{n}}$, праћена рефлексијом у равни која је окомита на њу, оставља молекул непромењеним. Такође се назива н-струка неправилна оса ротације, скраћено је С_н. Примери су присутни у тетраедарском силицијум тетрафлуориду, са три С₄ осе, и степеничастом конформацијом етана са једном С₆ осом. Оса С₁ одговара равни огледала σ, а оса С₂ је центар инверзије и. Молекул који нема С_н осу за било коју вредност н је хирални молекул.
• Идентитет, скраћено Е, од немачког 'Еинхеит' што значи јединство. Овај елемент симетрије се једноставно не састоји од промене: сваки молекул има овај елемент симетрије, који је еквивалентан C₁ правилној ротацији. Он мора бити укључен у листу елемената симетрије тако да формирају математичку групу, чија дефиниција захтева укључивање елемента идентитета. Тако се зове, јер је аналоган множењу са један (јединицом).

Операције

XеФ₄, са квадратном планарном геометријом, има 1 C₄ осу и 4 C₂ осе ортогоналне на C₄. Ових пет оса плус раван огледала нормална на осу C₄ дефинишу D_4х групу симетрије молекула.

Пет елемената симетрије повезују са собом пет типова симетријских операција, које остављају да се геометрија молекула не разликује од почетне геометрије. Понекад се разликују од елемената симетрије каретом или циркумфлексом. Стога, Ĉ_н је ротација молекула око осе, а Ê је операција идентитета. Елемент симетрије може имати више од једне операције симетрије повезане са њим. На пример, C₄ оса квадратног молекула ксенон тетрафлуорида (XеФ₄) повезана је са две Ĉ₄ ротације у супротним смеровима (90° и 270°), Ĉ₂ ротацијом (180°) и Ĉ₁ (0° или 360°). Пошто је Ĉ₁ еквивалентно Ê, Ŝ₁ са σ и Ŝ₂ са î, све операције симетрије се могу класификовати као исправне или неправилне ротације. За линеарне молекуле, ротација у смеру казаљке на сату или у супротном смеру око молекулске осе за било који угао Φ је операција симетрије.

Неправилна ротација С₄

Операције ротације-рефлексије за октаедарску симетрију

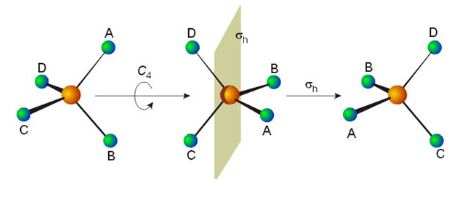
Групе симетрије

Групе

Операције симетрије молекула (или другог објекта) формирају групу. У математици, група је скуп са бинарном операцијом која задовољава четири својства наведена у наставку.

У групи симетрије, елементи групе су операције симетрије (не елементи симетрије), а бинарна комбинација се састоји од примене прво једне операције симетрије, а затим друге. Пример је секвенца C₄ ротације око з-осе и рефлексије у xy-равни, означене као σ(xy)C₄. По конвенцији редослед операција је с десна на лево.

Група симетрије следи дефинишућа својства било које групе.

1. Својство затворености:
   За сваки пар елемената x и y у Г, производ x*y је такође у Г.
   (у симболима, за свака два елемента x, y ∈ Г, x*y е такође у Г ).
   То значи да је група затворена тако да комбиновање два елемента не производи нове елементе. Операције симетрије имају ово својство јер ће низ од две операције произвести треће стање које се не разликује од другог, а самим тим и од првог, тако да је нето ефекат на молекул и даље операција симетрије. Ово се може илустровати помоћу табеле. На пример, са групом тачака C₃, постоје три операције симетрије: ротација за 120°, C₃, ротација за 240°, C₃² и ротација за 360°, што је еквивалентно идентичности, Е.

   

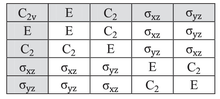
   Табела Ц2в множења групе тачака

   Група тачака C₃ Табела множења

   	Е	C3	C32
   Е	Е	C3	C32
   C3	C3	C32	Е
   C32	C32	Е	C3

2. Ова табела такође илуструје следећа својства
3. Асоцијативно својство:
   За свако x и y и з у Г, оба (x*y)*з и x*(y*з) резултирају истим елементом у Г.
   ( у симболима, (x*y)*з = x*(y*з ) за свако x, y, и з ∈ Г)
4. постојање својства идентитета:
   Мора постојати елемент ( рецимо е ) у Г такав да производ било ког елемента Г са е не мења елемент.
   ( у симболима, x*е = е*x = x за свако x ∈ Г )
5. постојање инверзног елемента:
   За сваки елемент x у Г, мора постојати елемент y у Г такав да је производ x и y елемент идентитета е.
   ( у симболима, за свако x ∈ Г постоји y ∈ Г такво да је x*y = y*x = е за свако x ∈ Г )

Редослед групе је број елемената у групи. За групе малих редова, својства групе могу се лако проверити разматрањем њене композиционе табеле, табеле чији редови и колоне одговарају елементима групе и чији уноси одговарају њиховим продуктима.

Групе тачака и групе пермутације-инверзије

Дијаграм тока за одређивање тачкасте групе молекула

Узастопна примена (или композиција) једне или више операција симетрије молекула има ефекат еквивалентан оном код неке појединачне операције симетрије молекула. На пример, C₂ ротација праћена σ_в рефлексијом се види као σ_в' операција симетрије: σ_в*C₂ = σ_в'. („Операција А праћена са Б у форму C“ пише се БА = C). Штавише, скуп свих операција симетрије (укључујући ову операцију композиције) поштује сва својства групе, дате горе. Дакле (С,*) је група, где је С скуп свих операција симетрије неког молекула, а * означава композицију (поновну примену) операција симетрије.

Ова група се назива група тачака тог молекула, јер скуп операција симетрије оставља најмање једну тачку фиксну (иако за неке симетрије цела оса или цела раван остаје фиксна). Другим речима, група тачке је група која сумира све операције симетрије које имају сви молекули у тој категорији. Насупрот томе, симетрија кристала је описана просторном групом операција симетрије, која укључује транслације у простору.

Операције симетрије групе тачака се могу одредити за одређени молекул узимајући у обзир геометријску симетрију његовог молекуларног модела. Међутим, када се користи тачкаста група за класификацију молекуларних стања, операције у њој се не тумаче на исти начин. Уместо тога, операције се тумаче као ротирајуће и/или да одражавају вибронске (вибрационо-електронске) координате и ове операције комутују са вибрационим Хамилтонијаном. То су „операције симетрије”" за тај вибрациони Хамилтонијан. Тачкаста група се користи за класификацију вибрационих сопствених стања крутог молекула по симетрији. Класификација симетрије ротационих нивоа, сопствених стања пуног (ротационо-вибрационо-електронског) Хамилтонијана, захтева употребу одговарајуће пермутационо-инверзионе групе коју је увео Лонгвет-Хигинс. Групе тачака описују геометријску симетрију молекула, док групе пермутације-инверзије описују енергетско инваријантну симетрију.

Примери група тачака

Додељивање групе тачака сваком молекулу класификује молекуле у категорије са сличним својствима симетрије. На пример, ПЦл₃, ПОФ₃, XеО₃, и НХ₃ сви деле идентичне операције симетрије. Сви они могу да се подвргну операцији идентитета Е, две различите C₃ операције ротације и три различите σ_в рефлексије у равни без промене њиховог идентитета, тако да су смештени у једну групу тачака, C_3в, са редоследом 6. Слично, вода (Х₂О) и водоник сулфид (Х₂С) такође деле идентичне операције симетрије. Оба молекула пролазе кроз операцију идентитета Е, једну C₂ ротацију и две σ_в рефлексије без промене идентитета, тако да су оба смештена у једну тачкасту групу, C_2в, са редоследом 4. Овај систем класификације помаже научницима да ефикасније проучавају молекуле, пошто хемијски сродни молекули у истој групи тачака имају тенденцију да показују сличне схеме везивања, дијаграме молекуларног везивања и спектроскопска својства. Симетрија групе тачака описује симетрију молекула када је фиксиран у својој равнотежној конфигурацији у одређеном електронском стању. Она не дозвољава тунелирање између минимума нити промену облика до којих може доћи услед ефеката центрифугалног изобличења молекуларне ротације.

Заједничке групе тачака

Следећа табела наводи многе групе тачака које се примењују на молекуле, означене помоћу Шоенфлајесове нотације, која је уобичајена у хемији и молекуларној спектроскопији. Описи укључују уобичајене облике молекула, који се могу објаснити ВСЕПР моделом. У сваком реду, описи и примери немају веће симетрије, што значи да именована група тачака обухвата све симетрије тачака.

Група тачака	Операције симетрије	Једноставан опис типичне геометрије	Пример 1	Пример 2	Пример 3
C1	Е	нема симетрије, хиралан	бромохлорофлуорометан (оба енантиомера су приказана)	лизергинска киселина	L-леуцин и већина других α-аминокиселина изузев глицина
Cс	Е σх	раван огледала	тионил хлорид	Хипохлораста киселина	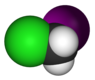хлоројодометан
Cи	Е и	инверзиони центар	месо-винска киселина	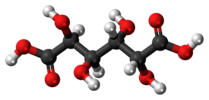муцична киселина (месо-галактаринска киселина)	1,2 дибромо 1,2 дихлороетан
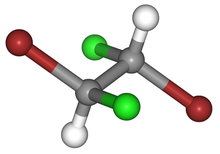C∞в	Е 2C∞Φ ∞σв	линеарна	флуороводоник (а сви остали хетеронуклеарни диатомски молекули)	азот-субоксид (диазот моноксид)	цијановодонична киселина (водоник цијанид)
D∞х	Е 2C∞Φ ∞σи и 2С∞Φ ∞C2	линеарна са инверзионим центром	оxyген (и сви други хомонуклеарни двоатомски молекули)	угљен диоксид	ацетилен (етин)
C2	Е C2	„геометрија отворене књиге”, хирална	водоник пероксид	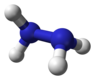хидразин	тетрахидрофуран (конформација увијања)
C3	Е C3 C32	пропелер, хирална	трифенилфосфин	триетиламин	фосфорна киселина
C2х	Е C2 и σх	раван са центром инверзије, без вертикалне равни	транс-1,2-дихлороетилен	транс-диазот дифлуорид	транс-азобензен
C2в	Е C2 σв(xз) σв'(yз)	угласта (Х2О) или тестераста (СФ4)	вода	сумпор тетрафлуорид	дихлорометан
C3х	Е C3 C32 σх С3 С35	пропелер	борна киселина	флороглуцинол (1,3,5-трихидроксибензен)	бензотрифуроксан
C3в	Е 2C3 3σв	тригонално пирамидална	амонијак (ако се занемари пиримидална инверзија)	фосфорил хлорид	кобалт тетракарбонил хидрид, ХЦо(ЦО)4
C4в	Е 2C4 C2 2σв 2σд	квадратно пирамидална	ксенон окситетрафлуорид	пентаборан(9), Б5Х9	нитропрусидни ањон [Фе(ЦН)5(НО)]2−
C5	Е 2C5 2C52	петерострука ротацијска симетрија	C-реактивни протеин	[Фе(Ме5-Цп)(П5)]	корануленски дериват
C5в	Е 2C5 2C52 5σв	комплекс 'столице за мужу'	циклопентадиенил никал нитрозил (ЦпНиНО)	коранулен	Пентаметилциклопентадиенил никал нитрозил (Цп*НиНО)
D2	Е C2(x) C2(y) C2(з)	заокрет, хирална	бифенил (искривљена конформација)	твистан (C10Х16)	(δ,δ)-транс-[Цо(ен)2Цл2]+
D3	Е C3(з) 3C2	троструки хеликс, хирална	Трис(етилендиамин)кобалт(III) катјон	трис(оксалат)гвожђе(III) ањон	трис(ен)кобалт(III)
D2х	Е C2(з) C2(y) C2(x) и σ(xy) σ(xз) σ(yз)	планарна са центром инверзије, вертикална раван	етилен	пиразин	диборан
D3х	Е 2C3 3C2 σх 2С3 3σв	тригонално планарна или тригонално бипирамидална	бор трифлуорид	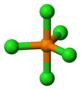фосфор пентахлорид	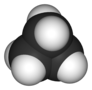циклопропан
D4х	Е 2C4 C2 2C2' 2C2" и 2С4 σх 2σв 2σд	квадратно планарна	ксенон тетрафлуорид	октахлородимолибдат(II) ањон	Транс-[ЦоIII(НХ3)4Цл2]+ (искључујући Х атоме)
D5х	Е 2C5 2C52 5C2 σх 2С5 2С53 5σв	пентагонална	циклопентадиенилни ањон	рутеноцен	C70
D6х	Е 2C6 2C3 C2 3C2' 3C2‘’ и 2С3 2С6 σх 3σд 3σв	хексагонална	бензен	бис(бензен)хром	коронен (C24Х12)
D7х	Е C7 С7 7C2 σх 7σв	хептагонална	тропилијум (C7Х7+) катјон
D8х	Е C8 C4 C2 С8 и 8C2 σх 4σв 4σд	октагонална	циклооктатетраенид (C8Х82−) анион	ураноцен	бис(кот)торијум(IV)
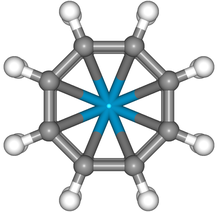D2д	Е 2С4 C2 2C2' 2σд	90° заокрет	ален	тетрасумпор тетранитрид	диборан(4) (побуђено стање)
D3д	Е 2C3 3C2 и 2С6 3σд	60° заокрет	етан (анти ротамер)	дикобалт октакарбонил (непремоштени изомер)	циклохексанска конформација столице
D4д	Е 2С8 2C4 2С83 C2 4C2' 4σд	45° заокрет	сумпор (конформација круне С8)	диманган декакарбонил (анти ротамер)	октафлуороксенатни јон (идеализована геометрија)
D5д	Е 2C5 2C52 5C2 и 2С103 2С10 5σд	36° заокрет	фероцен (анти ротамер)	Рутеноцен	фулеридни јон
С4	Е 2С4 C2		1,2,3,4-тетрафлуороспиропентан (мезо изомер)	тетраметил-кот	бис(дтх)бакар(I)
Тд	Е 8C3 3C2 6С4 6σд	тетраедрална	метан	фосфор пентоксид	адамантан
Тх	Е 4C3 4C32 и 3C2 4С6 4С65 3σх	пиритоедарска	[Фе(C5Х5Н)6]2+	[Тх(НО3)6]2-	Фе(Х2О)6
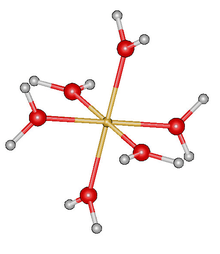Ох	Е 8C3 6C2 6C4 3C2 и 6С4 8С6 3σх 6σд	октаедарска или кубна	сумпор хексафлуорид	молибден хексакарбонил	кубан
I	Е 12C5 12C52 20C3 15C2	хирална икосаедарска или додекаедрска	риновирус	додекаедар	људски полио вирус
Iх	Е 12C5 12C52 20C3 15C2 и 12С10 12С103 20С6 15σ	икосаедарска или додекаедарска	букминстерфулерен	додекаборатни ањон	додекаедран

Репрезентације

Скуп матрица које се множе заједно на начин који опонаша табелу множења елемената групе назива се репрезентација групе. На пример, за C_2в групу тачака, следеће три матрице су део репрезентације групе:

$\underbrace {\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{C_{2}}\times \underbrace {\begin{bmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{bmatrix}} _{\sigma _{\text{v}}}=\underbrace {\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\\\end{bmatrix}} _{\sigma '_{\text{v}}}$

Иако постоји бесконачан број таквих репрезентација, несводљиве репрезентације (или „иррепс”) групе су све што је потребно, јер се све друге репрезентације група могу описати као линеарна комбинација несводљивих репрезентација. Такође, несводљиве репрезентације су оне матричне репрезентације у којима су матрице у свом најдијагоналнијем могућем облику.

Операције симетрије матрице трансформације

Табеле знакова

Главни чланак: Списак табела знакова за хемијски важне групе 3Д тачака

За било коју групу, њена табела ознака даје табеларни приказ (за класе групе) знакова (збир дијагоналних елемената) матрице свих несводљивих репрезентација групе. Како је број несводљивих репрезентација једнак броју класа, табела знакова је квадратна.

Репрезентације су означене у складу са сетом конвенција:

• А, када је ротација око главне осе симетрична
• Б, када је ротација око главне осе асиметрична
• Е и Т су двоструко и троструко дегенерисане репрезентације, респективно
• када група тачака има центар инверзије, индекс г (нем. gerade или уједначен) сигнализира да нема промене у предзнаку, а индекс у (унгераде или неуједначен) промену предзнака, у односу на инверзију.
• код група тачака C_∞в и D_∞х симболи су позајмљени из описа угаоног момента: Σ, Π, Δ.

Табеле такође обухватају информације о томе како се картезијански базни вектори, ротације око њих и њихове квадратне функције трансформишу операцијама симетрије групе, примећујући која се несводљива репрезентација трансформише на исти начин. Ове индикације су конвенционално на десној страни табеле. Ова информација је корисна, јер хемијски важне орбитале (посебно п и д орбитале) имају исте симетрије као ови ентитети.

Табела карактера за групу тачака симетрије C_2в је дата у наставку:

C2в	Е	C2	σв(xз)	σв'(yз)
А1	1	1	1	1	з	x2, y2, з2
А2	1	1	−1	−1	Рз	xy
Б1	1	−1	1	−1	x, Рy	xз
Б2	1	−1	−1	1	y, Рx	yз

Размотрите пример воде (Х₂О), која има C_2в симетрију описану изнад. Орбитала кисеоника од 2п_x има Б₁ симетрију као у четвртом реду табеле знакова изнад, са x у шестој колони). Она је оријентисана нормално на раван молекула и мења знак са C₂ и σ_в'(yз) операцијом, али остаје непромењена са друге две операције (очигледно, карактер за операцију идентитета је увек +1). Скуп знакова ове орбитале је стога {1, −1, 1, −1}, што одговара Б₁ несводљивој репрезентацији. Исто тако, види се да 2п_з орбитала има симетрију А_{1</суб несводљиве репрезентације (тј.: ниједна од операција симетрије је не мења), 2пy Б2 и 3дxy орбитала А2. Ове и друге назнаке су забележени у две крајње десне колоне табеле.}

Својства табеле знакова

Историјска позадина

Ханс Бете је користио ознаке операција тачкастих група у својој студији теорије поља лиганда 1929. године, а Јуџин Вигнер је користио теорију група да објасни правила селекције атомске спектроскопије. Прве табеле карактера саставио је Ласло Тиса (1933), у вези са вибрационим спектрима. Роберт Маликен је први објавио табеле карактера на енглеском (1933), а Е. Брајт Вилсон их је користио 1934. да предвиди симетрију вибрационих нормалних модова. Комплетан сет од 32 групе кристалографских тачака објавили су 1936. Розентал и Марфи.

Молекуларна ротација и молекуларна некрутост

Такође погледајте: Флуксиони молекул

Као што је горе објашњено у одељку Групе тачака и групе пермутације-инверзије, групе тачака су корисне за класификацију вибрационих и електронских стања крутих молекула (понекад се називају полукрути молекули) који пролазе само кроз мале осцилације око једне равнотежне геометрије. Лонгвет-Хигинс је увео општији тип групе симетрије погодан не само за класификацију вибрационих и електронских стања крутих молекула већ и за класификацију њихових ротационих и нуклеарних спинских стања. Даље, такве групе се могу користити за класификацију стања некрутих (или флуксионих) молекула који тунелирају између еквивалентних геометрија (које се називају верзије) и да би се омогућили ефекти изобличења молекуларне ротације. Ове групе су познате као пермутационо-инверзионе групе, јер су операције симетрије у њима енергетски изводљиве пермутације идентичних језгара, или инверзија у односу на центар масе (операција парности), или комбинација ова два.

На пример, етан (C₂Х₆) има три еквивалентне степеничасте конформације. Тунелирање између конформација се дешава на уобичајеним температурама унутрашњом ротацијом једне метил групе у односу на другу. Ово није ротација целог молекула око осе C₃. Иако свака конформација има D_3д симетрију, као у горњој табели, опис унутрашње ротације и повезаних квантних стања и нивоа енергије захтева потпунију пермутационо-инверзиону групу Г₃₆.

Слично, амонијак (НХ₃) има две еквивалентне пирамидалне (C_3в) конформације које се међусобно конвертују процесом познатим као азотна инверзија. Ово није операција инверзије групе тачака и која се користи за центросиметричне круте молекуле (тј. инверзија вибрационих померања и електронских координата у нуклеарном центру масе) пошто НХ₃ нема центар инверзије и није центросиметричан. Уместо тога, то је инверзија нуклеарних и електронских координата у молекуларном центру масе (понекад се назива операција парности), што је енергетски изводљиво за овај молекул. Одговарајућа пермутационо-инверзиона група која се користи у овој ситуацији је D_3х(M) која је изоморфна са групом тачака D_3х.

Поред тога, као примери, молекули метана (ЦХ₄) и Х₃⁺ имају високо симетричне равнотежне структуре са симетријама Т_д и D_3х тачка, респективно; недостају им трајни електрични диполни моменти, али имају веома слаб спектар чисте ротације због ротационог центрифугалног изобличења. Пермутационо-инверзионе групе потребне за комплетно проучавање ЦХ₄ и Х₃⁺ Т_д(M) и D_3х(M), респективно.

У свом основном (Н) електронском стању, молекул етилена C₂Х₄ има симетрију D_2х тачкасте групе, док у побуђеном (V) стању има D_2д симетрију. За третирање ова два стања заједно потребно је дозволити торзију и користити двоструку групу пермутационо-инверзионе групе Г₁₆.

Други и мање општ приступ симетрији нечврстих молекула је Алтманов допринос. У овом приступу групе симетрије су познате као Шредингерове супергрупе и састоје се од два типа операција (и њихових комбинација): (1) операције геометријске симетрије (ротације, рефлексије, инверзије) крутих молекула и (2) изодинамичке операције, које преводе нечврсти молекул у енергетски еквивалентан облик физички разумним процесом као што је ротација око једне везе (као у етану) или молекуларна инверзија (као у амонијаку).

Види још

• Паритет (физика) § Молекули
• Иредуцибилна репрезентација § Примене у теоријској физици и хемији
• Вудвард-Хофманова правила § Корелациони дијаграми
• Хаптичност § Хаптичност и променљивост
• Табела знакова
• Група кристалографских тачака
• Групе тачака у три димензије
• Симетрија двоатомских молекула
• Симетрија у квантној механици

Literatura

• Barnes, K.J. (2010). Group theory for the standard model and beyond. Series in high energy physics, cosmology, and gravitation. Taylor & Francis. ISBN 978-142-007-874-9. 
• Chaichian, M.; Hagedorn, R. (1998). Symmetry in quantum mechanics: From angular momentum to supersymmetry. Graduate student series in physics. Institute of physics (Bristol and Philadelphia). ISBN 0-7503-0408-1. 
• Hall, Brian C. (2013). Quantum Theory for Mathematicians. Graduate Texts in Mathematics. 267. Springer. Bibcode:2013qtm..book.....H. ISBN 978-1-4614-7115-8. S2CID 117837329. doi:10.1007/978-1-4614-7116-5. 
• Hall, Brian C. (2015). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Graduate Texts in Mathematics. 222 (2nd изд.). Springer. ISBN 978-3-319-13466-6. doi:10.1007/978-3-319-13467-3. 
• Haywood, S. (2011). Symmetries and Conservation Laws in Particle Physics: An Introduction to Group Theory for Particle Physicists. World Scientific. ISBN 978-184-816-703-2. 
• Ladd, M.F.C. (1989). Symmetry in molecules and crystals. Solid state science. Ellis Horwood series in physical chemistry. ISBN 0-85312-255-5. 
• Ludwig, W.; Falter, C. (1996). Symmetries in physics. Solid state science (2nd изд.). Springer. ISBN 3-540-60284-4. 
• Martin, B.R.; Shaw, G. (2013). Particle Physics. Manchester Physics Series (3rd изд.). Wiley. ISBN 978-0-470-03294-7. 
• McMahon, D. (2008). Quantum Field Theory. McGraw Hill. ISBN 978-0-07-154382-8. 
• Moretti, V. (2017). Spectral Theory and Quantum Mechanics; Mathematical Foundations of Quantum Theories, Symmetries and Introduction to the Algebraic Formulation. Unitext. 110 (2nd изд.). Springer. Bibcode:2017stqm.book.....M. ISBN 978-3-319-70705-1. S2CID 125121522. doi:10.1007/978-3-319-70706-8. 
• Reece, R.D. (2006). „A Derivation of the Quantum Mechanical Momentum Operator in the Position Representation”. 
• Soper, D.E. (2011). „Position and momentum in quantum mechanics” (PDF). 
• Porter, F. (2009). „Lie Groups and Lie Algebras” (PDF). Архивирано из оригинала (PDF) 2017-03-29. г. Приступљено 2013-06-05. 
• Mulders, P.J. (новембар 2011). „Quantum field theory” (PDF). Department of Theoretical Physics, VU University. 6.04. CS1 одржавање: Формат датума (веза)
• Hall, B.C. (2000). „An Elementary Introduction to Groups and Representations”. arXiv:math-ph/0005032 . 
• Quantum Mechanics, Third Edition: Non-Relativistic Theory (Volume 3)by L. D. Landau, L. M. Lifshitz; ISBN 978-0750635394 Едитион: 3рд; цхаптерс: XI анд XII.
• Пхyсицс оф Атомс & Молецулес бy Б.Х. Брансден, C.Ј. Јоацхаин; ISBN 978-8177582796 Едитион: 2нд едитион; цхаптер: 9
• Молецулар Спецтра анд Молецулар Струцтуре: Спецтра оф Диатомиц Молецулес бy Герхард Херзберг; ISBN 978-0894642685 Едитион: 2нд
• Молецулар Qуантум Мецханицс бy Петер W. Аткинс, Роналд С. Фриедман; ISBN 978-0199541423 Едитион: 5тх; цхаптер: 10.
• Лецтуре нотес он Qуантум Мецханицс (хандоутс: 12, 10) бy Проф. Соуренду Гупта, Тата Институте оф Фундаментал Ресеарцх, Мумбаи.
• Сyмметрy ин Пхyсицс: Принциплес анд Симпле Апплицатионс Волуме 1 бy Јамес Пхилип Еллиотт, П.Г. Даwбер; ISBN 978-0195204551
• А Модерн Аппроацх то Qуантум Мецханицс бy Јохн С. Тоwнсенд; Едитион 2нд; ISBN 978-1891389788
• Перкинс, Доналд Х. (2000). Интродуцтион то Хигх Енергy Пхyсицс. ИСБН 9780521621960. 
• Соззи, M. С. (2008). Дисцрете сyмметриес анд ЦП виолатион. Оxфорд Университy Пресс. ИСБН 978-0-19-929666-8. 
• Биги, I. I.; Санда, А. I. (2000). ЦП Виолатион. Цамбридге Монограпхс он Партицле Пхyсицс, Нуцлеар Пхyсицс анд Цосмологy. Цамбридге Университy Пресс. ИСБН 0-521-44349-0. 
• Wеинберг, С. (1995). Тхе Qуантум Тхеорy оф Фиелдс. Цамбридге Университy Пресс. ИСБН 0-521-67053-5. 
• Цоxетер, Х. С. M. (1974), „7 Тхе Бинарy Полyхедрал Гроупс”, Регулар Цомплеx Полyтопес, Цамбридге Университy Пресс, стр. 73–82 .
• Цоxетер, Х. С. M.; Мосер, W. О. Ј. (1980). Генераторс анд Релатионс фор Дисцрете Гроупс, 4тх едитион. Неw Yорк: Спрингер-Верлаг. ИСБН 0-387-09212-9.  6.5 Тхе бинарy полyхедрал гроупс, п. 68
• Цонwаy, Јохн Хортон; Хусон, Даниел Х. (2002), „Тхе Орбифолд Нотатион фор Тwо-Дименсионал Гроупс”, Струцтурал Цхемистрy, Спрингер Нетхерландс, 13 (3): 247—257, С2ЦИД 33947139, дои:10.1023/А:1015851621002 

Спољашње везе

• Групна симетрија тачака на Универзитету Њукасл
• Молекуларна симетрија на Империјалном колеџу Лондон
• Табеле симетрије групе молекулских тачака
• [хттпс://wеб.арцхиве.орг/wеб/20230328010349/хттпс://гернот-катзерс-спице-пагес.цом/цхарацтер_таблес/индеx.хтмл Архивирано на сајту Wayback Machine (28. март 2023) Табеле знакова за групе тачака за хемију]
• Молекуларна симетрија онлајн на Отвореном универзитету Израела
• Интернет курс предавања о молекуларној симетрији на Бергише универзитету
• ДЕЦОР – Симметрија @ Кембриџ кристалографски центар података
• Детаљи односа између група тачака и група пермутације-инверзије, Филип Бункер