Проширено хеширање

Овај чланак је започет или проширен кроз пројекат семинарских радова. Потребно је проверити превод, правопис и вики-синтаксу.
Када завршите са провером, допишете да након |проверено=.

Проширено хеширање је тип хасх система која третира хеш као бит стринг, и користи трие као резервисан простор за проналажење.^[1] Због хијерархијске природе система, ре-хашинг је постепена операција (ради једно резервисање у времену, по потреби). То значи да временски осетљиве операције су мање погођене растом табеле него стандардном хеш табелом.

Пример

Ово је пример узет из Фагин ет ал. 1979 харвнб грешка: више циљева (2×): ЦИТЕРЕФФагинНиевергелтПиппенгерСтронг1979 (хелп).

Претпостављајући да хеш функција $h(k)$ враћа бинарни број. Првих и бита сваког стринга ће се користити као индекси који ће усмеравати где ће они смештати у "директоријуму" (хеш табели). Поред тога и је најмањи број такав да су првих и бита свих чланова различити.

Коришћени кључеви:

$h(k_{1})$ = 100100

$h(k_{2})$ = 010110

$h(k_{3})$ = 110110

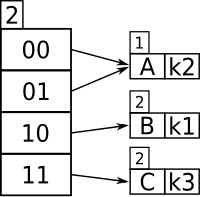
Нека претпоставимо да је за овај одређени пример, величина простора за смештање је 1. Прва два члана која се умећу, к1 и к2, разликују се по најзначајнијем биту, и уписују се у табелу као на слици:

Сада, ако к₃ треба да буде хеширан у табелу, неће бити довољно да распоредимо сва три члана водећи се само једним битом (зато што к₃ и к₁ имају исти први леви бит). Такође, јер је величина простора за смештања један, доћиће до прекорачења ширине простора за смештање. Зато ће поређење прва два најзначајнија бита дати сваком члану јединствену локацију, односно величина директоријума ће се дуплирати, као што се види на слици:

I сада к₁ и к₃ имају јединдтвене локације, бивајући распоређени према прва два најзначајнија лева бита. Зато што је к₂ у горњој половини табеле, оба поља и 00 и 01 указују на то, јер не постоји ниједан други члан за поређење који почиње са 0.

Даље објашњење

$h(k_{4})$ = 011110

Сада, к₄ треба да се убаци и његова прва два бита су 01..(1110) и користи 2 БИТА дубину у директоријуму, то показује од 01 ка простору за смештање А. Тај простор А је пун (максимална величина је 1), тако да мора мора да се прошири, зато што постоји више од једног показивача на простор А, нема потребе да се повећа величина директоријума. За то што је локална дубина простора А мања од глобалне дубине директоријума.

Шта је оно што би требало да знамо:

Број битова кључа у директоријуму (глобална дубина) и
Величина простора за смештање (локална дубина)

Постоје два важна случаја:

Дуплирање величине директоријума када је простор за смештање је пун.
Стварање новог простора за смештање, и поновно распоређивање унешених вредности из старог у стари и нови простор за смештање.

Испитујући почетни случај проширења хеш структуре, ако свако поље у директоријуму показује на један простот за смештање, онда би локална дубина требала бити једнака глобалној дубини.

Број поља у директоријуму једнак је 2^{глобална дубина}, почетни број простора за смештање је 2^{локална дубина}.

Ако је глобална дубина = локалној дубини = 0, онда је 2⁰ = 1, тако је почетни директоријум је један показивач на један простор за смештање.

Враћамо се на два стварна случаја:

Ако је локална дубина једнака глобалној дубини, онда постоји само један показивач на простор за смештање, и не постоје други директоријумски показивачи који могу показивати на простор за смештање, зато директоријум мора бити дуплиран (случај 1).

Ако је простор за смештање пун, ако је локална дубина мања од глобалне дубине онда постоји више од једног показивача од директоријума ка простору за смештање, и простор за смештање може бити дуплиран (случај 2)

Кључ 01 показује на Простор А , и локална дубина Простора А која је 1 је мања од глобане дубине директоријума која је 2, што значи да су кључеви који показују на Простор А распоређени користећи само први бит (нпр. 0), и Простор А мора да распореди свој садржај користећи 1 + 1 = 2 најважнија почетна бита. Уопштено, за сваки случај када је локална дубина д мања од глобалне D, д се мора повећати након дуплирања Простора за смештање, и ново д које означава број битова кључа који се користи за распоређивање вредности у стари и нови простор.

Сада, $h(k_{4})$ = 011110

је покушано поново, са два бита 01.., и сада кључ 01 показује на нови простор, али у њему је и даље к2 ( $h(k2)$ = 010110 такође почиње са 01).

Ако би к2 био 000110, са кључем 00, не би био проблем, зато што к2 би к2 остао у новом простору А’ и простор D би био празан.

( То би био најчешћи случај када су простори веће величине од 1 и нови дуплирани простори вероватно неће бити пуни, осим у случају да сви уноси ре-хеширају у један простор уместо да се расподеле у два. Како би повећали улогу дубине, пример ће бити испраћен логички до краја. )

Тако да Простор D мора бити дуплиран, али проверити његову локалну дубину, која је 2, која је иста као I глобална дубина, која је исто 2, тако да директоријум мора бити дуплиран поново, у циљу да садржи кључеве са довољно детаља, нпр. 3 бита.

Простор D мора да се дуплира судећи да је пун.
Пошто је локална дубина простора D једнака глобално дубини, директоријум се мора дуплирати како би се повећао број детаља, односно број битова, кључа.
Пошто се директоријум удвостручио глобална дубина се повећала на 3.
Нови унос к4 се поново хешира преко новог кључа, дужине 3 бита (нова глобална дубина) и завршава у D који има локалну дубину 2, који сада може бити промењен на 3 и D може бити подељен на Д’ и Е.
Садржај од D простора, к2, је поновно хеширан кључем од 3 бита и завршава у D.
к4 се поново хешира кључем од 3 бита и завршава у Е где постоји празно место.

Сада, $h(k2)$ = 010110 је у D и $h(k_{4})$ = 011110 је хеширан поново са 3 бита 011.., I смештен у простор D који је већ садржи к2, па је пун. Локална дубина простора D је 2, али је глобална дубина 3, када се директоријум дуплирао, па сада D може бити подељен у просторе Д’ и Е, саџај простора D, к2 је $h(k2)$ који се поново хешира са бит кључем дужине једнаке новој глобалној дубини, а то је 3, и к2 завршава у D'. Онда нови унос к4 се поново хеширана коришћењем нове глобалне дубине која је 3, односно кључем од 3 бита, и то нам даје 011 који сада упада у нови простор Е, који је празан. Тако да к4 иде у простор Е.

Пример имплементације

Испод се налази алагоритам проширеног хеширања написан у језику Пyтхон. Напомена: Проблем постоји ако дубине превазиђу битску величину интиџера, јер тада удвостручивање директоријума или подела простора за смештање неће дозволити да се унешене вредности поново хеширају у различите просторе за смештање.

Код користи леаст сигнифицант битс, што чини да се што ефикасније проширује табела, као што је да се цео директоријум копира у блок.(Рамакрисхнан & Гехрке 2003).

Пyтхон пример

PAGE_SZ = 20

class Page(object):

    def __init__(self):
        self.m = {}
        self.d = 0

    def full(self):
        return len(self.m) >= PAGE_SZ

    def put(self,k,v):
        self.m[k] = v

    def get(self,k):
        return self.m.get(k)

class EH(object):

    def __init__(self):
        self.gd = 0 
        p = Page()
        self.pp= [p]

    def get_page(self,k):
        h = hash(k) 
        p = self.pp[ h & (( 1 << self.gd) -1)]
        return p

    def  put(self, k, v):
        p = self.get_page(k)
        if p.full() and p.d == self.gd:
            self.pp *= 2
            self.gd += 1
        
        if p.full() and p.d < self.gd:
            p.put(k,v);
            p1 = Page()
            p2 = Page()
            for k2,v2 in p.m.items():
                h = hash(k2)
                h = h & ((1 << self.gd) -1)
                if (h >> p.d) & 1 == 1:
                    p2.put(k2,v2)
                else:
                    p1.put(k2,v2)
            for i,x in enumerate(self.pp):
                if x == p:
                    if (i >> p.d) & 1 == 1:
                        self.pp[i] = p2
                    else:
                        self.pp[i] = p1

            p2.d = p1.d = p.d + 1
        else:    
            p.put(k,  v)

    def get(self, k):
        p = self.get_page(k)
        return p.get(k)

if __name__ == "__main__":
    eh = EH()
    N = 10088
    l = list(range(N))

    import random
    random.shuffle(l)
    for x in l:
        eh.put(x,x)
    print l

    for i in range(N):
        print eh.get(i)

Референце

^ Фагин, Р.; Ниевергелт, Ј.; Пиппенгер, Н.; Стронг, Х. Р. (септембар 1979), „Еxтендибле Хасхинг - А Фаст Аццесс Метход фор Дyнамиц Филес”, АЦМ Трансацтионс он Датабасе Сyстемс, 4 (3): 315—344, дои:10.1145/320083.320092

Види још

Референце

Фагин, Р.; Ниевергелт, Ј.; Пиппенгер, Н.; Стронг, Х. Р. (септембар 1979), „Еxтендибле Хасхинг - А Фаст Аццесс Метход фор Дyнамиц Филес”, АЦМ Трансацтионс он Датабасе Сyстемс, 4 (3): 315—344, дои:10.1145/320083.320092
Рамакрисхнан, Р.; Гехрке, Ј. (2003), Датабасе Манагемент Сyстемс, 3рд Едитион: Цхаптер 11, Хасх-Басед Индеxинг, стр. 373—378

Спољашње везе на енглеском језику

Paul E. Black, Extendible hashing at the National Institute of Standards and Technology, Dictionary of Algorithms and Data Structures.
Еxтендибле Хасхинг Архивирано на сајту Wayback Machine (5. август 2014) ат Университy оф Небраска
Еxтендибле Хасхинг нотес ат Аркансас Стате Университy
Еxтендибле хасхинг нотес Архивирано на сајту Wayback Machine (3. март 2016)

[1] Фагин, Р.; Ниевергелт, Ј.; Пиппенгер, Н.; Стронг, Х. Р. (септембар 1979), „Еxтендибле Хасхинг - А Фаст Аццесс Метход фор Дyнамиц Филес”, АЦМ Трансацтионс он Датабасе Сyстемс, 4 (3): 315—344, дои:10.1145/320083.320092

[1]