Prošireno heširanje

Prošireno heširanje je tip hash sistema koja tretira heš kao bit string, i koristi trie kao rezervisan prostor za pronalaženje. Zbog hijerarhijske prirode sistema, re-hašing je postepena operacija (radi jedno rezervisanje u vremenu, po potrebi). To znači da vremenski osetljive operacije su manje pogođene rastom tabele nego standardnom heš tabelom.

Primer

Ovo je primer uzet iz Fagin et al. 1979.

Pretpostavljajući da heš funkcija $h(k)$ vraća binarni broj. Prvih i bita svakog stringa će se koristiti kao indeksi koji će usmeravati gde će oni smeštati u "direktorijumu" (heš tabeli). Pored toga i je najmanji broj takav da su prvih i bita svih članova različiti.

Korišćeni ključevi:

$h(k_{1})$ = 100100

$h(k_{2})$ = 010110

$h(k_{3})$ = 110110

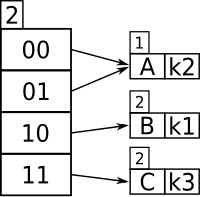
Neka pretpostavimo da je za ovaj određeni primer, veličina prostora za smeštanje je 1. Prva dva člana koja se umeću, k1 i k2, razlikuju se po najznačajnijem bitu, i upisuju se u tabelu kao na slici:

Sada, ako k₃ treba da bude heširan u tabelu, neće biti dovoljno da rasporedimo sva tri člana vodeći se samo jednim bitom (zato što k₃ i k₁ imaju isti prvi levi bit). Takođe, jer je veličina prostora za smeštanja jedan, doćiće do prekoračenja širine prostora za smeštanje. Zato će poređenje prva dva najznačajnija bita dati svakom članu jedinstvenu lokaciju, odnosno veličina direktorijuma će se duplirati, kao što se vidi na slici:

I sada k₁ i k₃ imaju jedindtvene lokacije, bivajući raspoređeni prema prva dva najznačajnija leva bita. Zato što je k₂ u gornjoj polovini tabele, oba polja i 00 i 01 ukazuju na to, jer ne postoji nijedan drugi član za poređenje koji počinje sa 0.

Dalje objašnjenje

$h(k_{4})$ = 011110

Sada, k₄ treba da se ubaci i njegova prva dva bita su 01..(1110) i koristi 2 BITA dubinu u direktorijumu, to pokazuje od 01 ka prostoru za smeštanje A. Taj prostor A je pun (maksimalna veličina je 1), tako da mora mora da se proširi, zato što postoji više od jednog pokazivača na prostor A, nema potrebe da se poveća veličina direktorijuma. Za to što je lokalna dubina prostora A manja od globalne dubine direktorijuma.

Šta je ono što bi trebalo da znamo:

1. Broj bitova ključa u direktorijumu (globalna dubina) i
2. Veličina prostora za smeštanje (lokalna dubina)

Postoje dva važna slučaja:

1. Dupliranje veličine direktorijuma kada je prostor za smeštanje je pun.
2. Stvaranje novog prostora za smeštanje, i ponovno raspoređivanje unešenih vrednosti iz starog u stari i novi prostor za smeštanje.

Ispitujući početni slučaj proširenja heš strukture, ako svako polje u direktorijumu pokazuje na jedan prostot za smeštanje, onda bi lokalna dubina trebala biti jednaka globalnoj dubini.

Broj polja u direktorijumu jednak je 2^{globalna dubina}, početni broj prostora za smeštanje je 2^{lokalna dubina}.

Ako je globalna dubina = lokalnoj dubini = 0, onda je 2⁰ = 1, tako je početni direktorijum je jedan pokazivač na jedan prostor za smeštanje.

Vraćamo se na dva stvarna slučaja:

Ako je lokalna dubina jednaka globalnoj dubini, onda postoji samo jedan pokazivač na prostor za smeštanje, i ne postoje drugi direktorijumski pokazivači koji mogu pokazivati na prostor za smeštanje, zato direktorijum mora biti dupliran (slučaj 1).

Ako je prostor za smeštanje pun, ako je lokalna dubina manja od globalne dubine onda postoji više od jednog pokazivača od direktorijuma ka prostoru za smeštanje, i prostor za smeštanje može biti dupliran (slučaj 2)

Ključ 01 pokazuje na Prostor A , i lokalna dubina Prostora A koja je 1 je manja od globane dubine direktorijuma koja je 2, što znači da su ključevi koji pokazuju na Prostor A raspoređeni koristeći samo prvi bit (npr. 0), i Prostor A mora da rasporedi svoj sadržaj koristeći 1 + 1 = 2 najvažnija početna bita. Uopšteno, za svaki slučaj kada je lokalna dubina d manja od globalne D, d se mora povećati nakon dupliranja Prostora za smeštanje, i novo d koje označava broj bitova ključa koji se koristi za raspoređivanje vrednosti u stari i novi prostor.

Sada, $h(k_{4})$ = 011110

je pokušano ponovo, sa dva bita 01.., i sada ključ 01 pokazuje na novi prostor, ali u njemu je i dalje k2 ($h(k2)$ = 010110 takođe počinje sa 01).

Ako bi k2 bio 000110, sa ključem 00, ne bi bio problem, zato što k2 bi k2 ostao u novom prostoru A’ i prostor D bi bio prazan.

( To bi bio najčešći slučaj kada su prostori veće veličine od 1 i novi duplirani prostori verovatno neće biti puni, osim u slučaju da svi unosi re-heširaju u jedan prostor umesto da se raspodele u dva. Kako bi povećali ulogu dubine, primer će biti ispraćen logički do kraja. )

Tako da Prostor D mora biti dupliran, ali proveriti njegovu lokalnu dubinu, koja je 2, koja je ista kao I globalna dubina, koja je isto 2, tako da direktorijum mora biti dupliran ponovo, u cilju da sadrži ključeve sa dovoljno detalja, npr. 3 bita.

1. Prostor D mora da se duplira sudeći da je pun.
2. Pošto je lokalna dubina prostora D jednaka globalno dubini, direktorijum se mora duplirati kako bi se povećao broj detalja, odnosno broj bitova, ključa.
3. Pošto se direktorijum udvostručio globalna dubina se povećala na 3.
4. Novi unos k4 se ponovo hešira preko novog ključa, dužine 3 bita (nova globalna dubina) i završava u D koji ima lokalnu dubinu 2, koji sada može biti promenjen na 3 i D može biti podeljen na D’ i E.
5. Sadržaj od D prostora, k2, je ponovno heširan ključem od 3 bita i završava u D.
6. k4 se ponovo hešira ključem od 3 bita i završava u E gde postoji prazno mesto.

Sada, $h(k2)$ = 010110 je u D i $h(k_{4})$ = 011110 je heširan ponovo sa 3 bita 011.., I smešten u prostor D koji je već sadrži k2, pa je pun. Lokalna dubina prostora D je 2, ali je globalna dubina 3, kada se direktorijum duplirao, pa sada D može biti podeljen u prostore D’ i E, sadžaj prostora D, k2 je $h(k2)$ koji se ponovo hešira sa bit ključem dužine jednake novoj globalnoj dubini, a to je 3, i k2 završava u D'. Onda novi unos k4 se ponovo heširana korišćenjem nove globalne dubine koja je 3, odnosno ključem od 3 bita, i to nam daje 011 koji sada upada u novi prostor E, koji je prazan. Tako da k4 ide u prostor E.

Primer implementacije

Ispod se nalazi alagoritam proširenog heširanja napisan u jeziku Python. Napomena: Problem postoji ako dubine prevaziđu bitsku veličinu intidžera, jer tada udvostručivanje direktorijuma ili podela prostora za smeštanje neće dozvoliti da se unešene vrednosti ponovo heširaju u različite prostore za smeštanje.

Kod koristi least significant bits, što čini da se što efikasnije proširuje tabela, kao što je da se ceo direktorijum kopira u blok.(Ramakrishnan & Gehrke 2003).

Python primer

PAGE_SZ = 20

class Page(object):

    def __init__(self):
        self.m = {}
        self.d = 0

    def full(self):
        return len(self.m) >= PAGE_SZ

    def put(self,k,v):
        self.m[k] = v

    def get(self,k):
        return self.m.get(k)

class EH(object):

    def __init__(self):
        self.gd = 0 
        p = Page()
        self.pp= [p]

    def get_page(self,k):
        h = hash(k) 
        p = self.pp[ h & (( 1 << self.gd) -1)]
        return p

    def  put(self, k, v):
        p = self.get_page(k)
        if p.full() and p.d == self.gd:
            self.pp *= 2
            self.gd += 1
        
        if p.full() and p.d < self.gd:
            p.put(k,v);
            p1 = Page()
            p2 = Page()
            for k2,v2 in p.m.items():
                h = hash(k2)
                h = h & ((1 << self.gd) -1)
                if (h >> p.d) & 1 == 1:
                    p2.put(k2,v2)
                else:
                    p1.put(k2,v2)
            for i,x in enumerate(self.pp):
                if x == p:
                    if (i >> p.d) & 1 == 1:
                        self.pp[i] = p2
                    else:
                        self.pp[i] = p1

            p2.d = p1.d = p.d + 1
        else:    
            p.put(k,  v)

    def get(self, k):
        p = self.get_page(k)
        return p.get(k)

if __name__ == "__main__":
    eh = EH()
    N = 10088
    l = list(range(N))

    import random
    random.shuffle(l)
    for x in l:
        eh.put(x,x)
    print l

    for i in range(N):
        print eh.get(i)

Vidi još

• Trie
• Heš tabela
• Linearno heširanje
• Dvostruko heširanje

Reference

• Fagin, R.; Nievergelt, J.; Pippenger, N.; Strong, H. R. (septembar 1979), „Extendible Hashing - A Fast Access Method for Dynamic Files”, ACM Transactions on Database Systems, 4 (3): 315—344, doi:10.1145/320083.320092 
• Ramakrishnan, R.; Gehrke, J. (2003), Database Management Systems, 3rd Edition: Chapter 11, Hash-Based Indexing, стр. 373—378 

Spoljašnje veze na engleskom jeziku

• Paul E. Black, Extendible hashing at the National Institute of Standards and Technology, Dictionary of Algorithms and Data Structures.
• Extendible Hashing Архивирано на сајту Wayback Machine (5. август 2014) at University of Nebraska
• Extendible Hashing notes at Arkansas State University
• Extendible hashing notes Архивирано на сајту Wayback Machine (3. март 2016)