Учење без надзора

Учење без надзора је метода у машинском учењу где, за разлику од учења под надзором, алгоритми уче обрасце искључиво из неозначених података. Очекује се да ће кроз мимикрију, која је важан начин учења код људи, машина бити принуђена да изгради концизан приказ свог света, а затим из њега генерише имагинативе садржај.

Друге методе у спектру надзора су подржано учење где се машини даје само нумеричка оцена перформанси као смерница, и слаб или полунадзор где је мали део података означен и самонадзиран.

Неуронске мреже

Задаци наспрам метода

Тенденција да се за задатак користе методе под надзором наспрам ненадгледаних. Називи задатака прелазе границе круга намерно. То показује да је класична подела маштовитих задатака (лево) коришћењем метода без надзора замагљена у данашњим шемама учења.

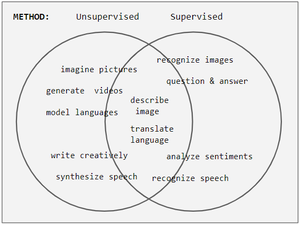
Задаци неуронске мреже се често категоришу као дискриминативни (препознавање) или генеративни (имагинација). Често, али не увек, дискриминативни задаци користе надгледане методе, а генеративни задаци користе ненадгледане (погледајте Венов дијаграм); међутим, раздвајање је веома магловито. На пример, препознавање објеката фаворизује надгледано учење, али учење без надзора такође може групирати објекте у групе. Штавише, како прогресс напредује, неки задаци користе обе методе, а неки задаци прелазе од једних до других. На пример, препознавање слика је почело као претежно надгледано, али је постало хибридно коришћењем ненадзиране претходне обуке, а затим је поново кренуло ка надзору са појавом елиминације, РеЛУ-а и адаптивних стопа учења.

Тренинг

Током фазе учења, мрежа без надзора покушава да опонаша податке који су јој дати и користи грешку у свом опонашаном излазу да се исправи (тј. исправи своје пондере и пристраности). Понекад се грешка изражава као ниска вероватноћа да дође до погрешног излаза, или се може изразити као нестабилно стање високе енергије у мрежи.

За разлику од доминантне употребе бекпропагације од стране надгледаних метода, ненадгледано учење такође користи друге методе укључујући: Хопфиелдово правило учења, Болцманово правило учења, контрастивну дивергенцију, будно спавање, варијационо закључивање, максималну вероватноћу, максимална апостериорну процена, Гибсово узорковање и грешке бекпропагационе реконструкције или репараметаризације скривеног стања. Погледајте табелу испод за више детаља.

Енергија

Енергетска функција је макроскопска мера активационог стања мреже. У Болцмановим машинама она игра улогу функције трошкова. Ова аналогија са физиком инспирисана је анализом макроскопске енергије гаса Лудвига Болцмана из микроскопских вероватноћа кретања честица $p\propto e^{-E/kT}$ , где је к Болцманова константа, а Т је температура. У РБМ мрежи релација је $p=e^{-E}/Z$ ,^[1] где $p$ и $E$ варирају у свим могућим активациони обрасцима и $\textstyle {Z=\sum _{\scriptscriptstyle {\text{All Patterns}}}e^{-E({\text{pattern}})}}$ . Прецизније, $p(a)=e^{-E(a)}/Z$ , где је $a$ образац за активирање свих неурона (видљивих и скривених). Отуда неке ране неуронске мреже носе назив Болцманова машина. Пол Смоленски назива $-E\,$ хармонијом. Мрежа настоји да оствари ниску енергију која је висока хармонија.

Мреже

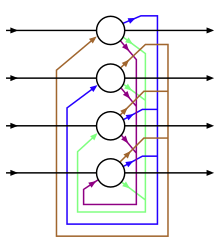
Ова табела приказује дијаграме повезивања различитих ненадзираних мрежа, чији ће детаљи бити дати у одељку о поређењу мрежа. Кругови су неурони, а ивице између њих су пондерисане везе. Како се дизајн мреже мења, додају се функције које омогућавају нове могућности или се уклањају како би учење било брже. На пример, неурони се мењају између детерминистичког (Хопфилд) и стохастичког (Болцман) да би омогућили робустан излаз, тежине се уклањају унутар слоја (РБМ) да би се убрзало учење, или је дозвољено да везе постану асиметричне (Хелмхолц).

Хопфилд	Болцман	РБМ	Сложени Болцман
Мрежа заснована на магнетним доменима у гвожђу са једним самоповезаним слојем. Може се користити као адресабилна меморија за садржај.	Мрежа је подељена на 2 слоја (скривена вс. видљива), али и даље користи симетричне двосмерне тежине. Пратећи Болцманову термодинамику, појединачне вероватноће стварају макроскопске енергије.	Ограничена Болцманова машина. Ово је Болцманова машина у којој су бочне везе унутар слоја забрањене да би анализа била сводљива.	Ова мрежа има више РБМ-ова за кодирање хијерархије скривених карактеристика. Након што је један РБМ обучен, додаје се још један плави скривени слој (види леви РБМ), а горња 2 слоја се обучавају као црвени и плави РБМ. Тако се средњи слојеви РБМ-а понашају као скривени или видљиви, у зависности од фазе обуке у којој се налазе.

Хелмхолц	Аутоинкодер	ВАЕ
Уместо двосмерне симетричне везе наслаганих Болцманових машина, присутне су одвојене једносмерне везе да бе формирала петљу. То се користи за генерацију и дискриминацију.	Мрежа унапред која има за циљ да пронађе добру репрезентацију средњег слоја свог улазног света. Ова мрежа је детерминистичка, тако да није једнако робусна као њен наследник ВАЕ.	Примењује варијационо резоновање на аутоматски кодер. Средњи слој је ссет средњих вредности и варијанси за Гаусове дистрибуције. Стохастичка природа омогућава робустнију имагинацију од детерминистичког аутоенкодера.

Од мрежа које носе имена људи, само је Хопфилд радио директно са неуронским мрежама. Болцман и Хелмхолц су живели пре ере вештачких неуронских мрежа, али је њихов рад у физици и физиологији инспирисао аналитичке методе које су кориштене.

Историја

1969	Перцептрони Минског & Паперта показују да перцептрон без скривених слојева не успева на XОР-у
1970-те	(приближни датуми) Прва АИ зима
1974	Изингов магнетни модел који је предложио ВА Литл за спознају
1980	Фукушима уводи неокогнитрон, који је касније назван конволуциона неуронска мрежа. Углавном се користи у СЛ, али заслужује да се помене.
1982	Изингова варијанта Хопфилдове мреже коју је Џон Хопфилд описао као ЦАМ и класификатори.
1983	Изингова варијанта Болцманове машине са пробабилистичким неуронима које су описали Хинтон и Сејновски након Шерингтоновог и Киркпатриковог рада из 1975. године.
1986	Пол Смоленски објављује теорију хармоније, која је РБМ са практично истом Болцмановом енергетском функцијом. Смоленски није дао шему практичне обуке. Хинтон је то учинио средином 2000-их.
1995	Шмитубер уводи ЛСТМ неурон за језике.
1995	Дајан & Хинтон представљају Хелмхолцову машину
1995-2005	(приближни датуми) Друга АИ зима
2013	Кингма, Резенде, & цо. су увели варијантне аутокодере као Бајесову графичку мрежу вероватноће, са неуронским мрежама као компонентама.

Специфичне мреже

Овде су итакнуте неке од карактеристика одабраног сета мрежа.

Хопфилдова мрежа: Феромагнетизам је инспирисао Хопфилдове мреже. Неурону одговара домен гвожђа са бинарним магнетним моментима горе и доле, а неуронске везе одговарају утицају домена једни на друге. Симетричне везе омогућавају глобалну енергетску формулацију. Током закључивања, мрежа ажурира свако стање користећи стандардну функцију корака активације. Симетрични пондери и праве енергетске функције гарантују конвергенцију до стабилног обрасца активације. Асиметричне тежине је тешко анализирати. Хопфилдове мреже се користе као Адресабилне меморије садржаја (ЦАМ).
Болцманова машина: Ово су стохастичке Хопфилдове мреже. Њихова вредност стања је узоркована из овог пдф-а на следећи начин: претпоставимо да се бинарни неурон активира са Бернулијевом вероватноћом п(1) = 1/3 и почива са п(0) = 2/3. Од њега се узоркује узимањем равномерно распоређеног случајног броја y, и укључивањем у инвертирану кумулативну функцију расподеле, што је у овом случају функција корака са прагом 2/3. Инверзна функција = { 0 иф x <= 2/3, 1 иф x > 2/3 }.
Мрежа сигмоидног уверења: Уведена од стране Радфорда Нила 1992. године, ова мрежа примењује идеје из пробабилистичких графичких модела на неуронске мреже. Кључна разлика је у томе што чворови у графичким моделима имају унапред додељена значења, док се карактеристике неурона мрежа веровања одређују након обуке. Мрежа је ретко повезани усмерени ациклични граф састављен од бинарних стохастичких неурона. Правило учења потиче од максималне вероватноће на п(X): Δw_иј $\propto$ с_ј * (с_и - п_и), где је п_и = 1 / ( 1 + е^{пондерисани улази у неурон и} ). с_ј су активације из непристрасног узорка постериорне дистрибуције и то је проблематично због проблема објашњавања који је покренуо Јудеа Перл. Варијабилне Бајесове методе користе сурогат постериор и очигледно занемарују ову сложеност.
Мрежа дубоких уверења: Уведена од стране Хинтона, ова мрежа је хибрид РБМ-а и мреже сигмоидног веровања. Горња 2 слоја су РБМ, а други слој према доле формира сигмоидну мрежу веровања. Један га тренира методом наслаганог РБМ-а, а затим одбацује пондере за препознавање испод горњег РБМ-а. Према подацима из 2009. године, сматра се да је 3-4 слоја оптимална дубина.^[2]
Хелмхолцова машина: Ово су ране инспирације за варијационе аутоматске енкодере. Његове 2 мреже комбиноване у пондере облика један—напред управљају препознавањем, а пондери уназад имплементирају имагинацију. То је можда прва мрежа која ради и једно и друго. Хелмхолц није радио на машинском учењу, али је инспирисао поглед на „машину статистичког закључивања чија је функција да закључи вероватне узроке сензорног уноса“.^[3] Стохастички бинарни неурон даје вероватноћу да је његово стање 0 или 1. Унос података се обично не сматра слојем, али у режиму генерисања Хелмхолцове машине, слој података прима улаз из средњег слоја и има одвојене пондере за ову сврху, те се сматра слојем. Стога ова мрежа има 3 слоја.
Вариацијски аутокодер: Они су инспирисани Хелмхолцовим машинама и комбинују пробабилистичку мрежу са неуронским мрежама. Аутокодер је трослојна ЦАМ мрежа, где би средњи слој требало да буде нека интерна репрезентација улазних образаца. Неурална мрежа кодера је дистрибуција вероватноће q_φ(з гивен x), а мрежа декодера је п_θ(x гивен з). Пондери се називају фи & тета, а не W и V као код Хелмхолца, што је козметичка разлика. Ове 2 мреже могу бити потпуно повезане, или могу користити другачије НН шему.

Референце

^ Хинтон, Г. (2012). „А Працтицал Гуиде то Траининг Рестрицтед Болтзманн Мацхинес” (ПДФ). Неурал Нетwоркс: Трицкс оф тхе Траде. Лецтуре Нотес ин Цомпутер Сциенце. 7700. Спрингер. стр. 599—619. ИСБН 978-3-642-35289-8. дои:10.1007/978-3-642-35289-8_32.
^ Хинтон, Геоффреy (септембар 2009). „Дееп Белиеф Нетс” (видео).
^ Петер, Даyан; Хинтон, Геоффреy Е.; Неал, Радфорд M.; Земел, Рицхард С. (1995). „Тхе Хелмхолтз мацхине.”. Неурал Цомпутатион. 7 (5): 889—904. ПМИД 7584891. С2ЦИД 1890561. дои:10.1162/нецо.1995.7.5.889. хдл:21.11116/0000-0002-Д6Д3-Е .

Литература

Боусqует, О.; вон Луxбург, У.; Раетсцх, Г., ур. (2004). Адванцед Лецтурес он Мацхине Леарнинг. Спрингер. ИСБН 978-3540231226.
Дуда, Рицхард О.; Харт, Петер Е.; Сторк, Давид Г. (2001). „Унсупервисед Леарнинг анд Цлустеринг”. Паттерн цлассифицатион (2нд изд.). Wилеy. ИСБН 0-471-05669-3.
Хастие, Тревор; Тибсхирани, Роберт; Фриедман, Јероме (2009). „Унсупервисед Леарнинг”. Тхе Елементс оф Статистицал Леарнинг: Дата мининг, Инференце, анд Предицтион. Спрингер. стр. 485—586. ИСБН 978-0-387-84857-0. дои:10.1007/978-0-387-84858-7_14.
Хинтон, Геоффреy; Сејноwски, Терренце Ј., ур. (1999). Унсупервисед Леарнинг: Фоундатионс оф Неурал Цомпутатион. МИТ Пресс. ИСБН 0-262-58168-X.

[Hinton2010-1] Хинтон, Г. (2012). „А Працтицал Гуиде то Траининг Рестрицтед Болтзманн Мацхинес” (ПДФ). Неурал Нетwоркс: Трицкс оф тхе Траде. Лецтуре Нотес ин Цомпутер Сциенце. 7700. Спрингер. стр. 599—619. ИСБН 978-3-642-35289-8. дои:10.1007/978-3-642-35289-8_32.

[HintonMlss2009-2] Хинтон, Геоффреy (септембар 2009). „Дееп Белиеф Нетс” (видео).

[“nc95“-3] Петер, Даyан; Хинтон, Геоффреy Е.; Неал, Радфорд M.; Земел, Рицхард С. (1995). „Тхе Хелмхолтз мацхине.”. Неурал Цомпутатион. 7 (5): 889—904. ПМИД 7584891. С2ЦИД 1890561. дои:10.1162/нецо.1995.7.5.889. хдл:21.11116/0000-0002-Д6Д3-Е .

[1]

[2]

[3]