Greška za jedan

Greška za jedan (OBOE), je često poznat kao OBOB (bag za jedan), je logička greška koja uključuje diskretnu jednakost uslova granica. Često se aktivira u programiranju kada se ponavlja upravljanje tokom kada se ponavlja jednom suvišno ili premalo. Ovaj problem se može podići kada programer napravi grešku koristeći " manje od ili jednako" gde "manje od " bi trebalo da se koristi u poređenju ili greškama da odvede do profila koji sekvenca startuje na nuli više nego jednom (kao što je sa indeksima reda u mnogim jezicima). Ovo se može pojaviti i u matematičkom kontekstu.

Petljanje nad redovima

Razmotriti niz članova, i članove m kroz n (zaključno) koji će biti procesovani. Koliko je članova tamo? Intuitivni odgovor može biti n - m, ali to je greška za jedan, koji pokazuje grešku ograđena poruka; tačan odgovor je n –m + 1.

Iz ovog razloga, opseg u računarstvu je često predstavljen preko poluotvorenih intervala; opseg od m do n (zaključno) je predstavljen opsegomod m (zaključno do n + 1 (nezaključno) kako bi se izbegle greške ograđene poruke. Na primer, petlja koja se ponavlja 5 puta može biti zapisana kao poluotvoreni interval od 0 do 5:

for (i = 0; i < 5; i++) 
{
    /* Тело петље */
}

Telo petlje je izvršeno preko i jednako sa 0; i onda postaje 1, 2, 3, i na kraju 4 pri uspešnim ponavljanjima. U tom trenutku, i postaje5, tako da i < 5 je netačno i petlja se završava. Međutim, ako je ovo poređenje korišćeno <= (manje ili jednako), petlja bi se izvršila šest puta: i uzima vrednosti 0, 1, 2, 3, 4, i 5. Isto tako, ako je i postavljeno na 1 a ne na 0, bilo bi samo 4 ponavljanja: i uzima vrednosti 1, 2, 3, i 4. Obe ove alternative mogu biti uzrok greške za jedan.

Još jedna ovakva greška se može desiti ako se do while petlja koristi umesto while petlje(ili obrnuto). Do wihle petlja garantuje da će raditi samo jednom.

Povezana sa redom konfuzija može takođe rezultovati iz razlika u programskim jezicima. Brojanje od 0 je najčešće, ali neki jezici počinju brojanje od 1. Paskal ima nizove sa indeksima definisanim preko korisnika. Ovo omogućuje da se modeluju indeksi niza posle domena problema.

Greška ograđene poruke

Ograda sa n sekcija ima n+1 posta.

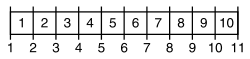
Greška ograđene poruke (obično se naziva stub telegrafa ili greška poruke lampe ) je specijalan tip greške za jedan. Sledeći problem ilustruje grešku.

Intuitivni odgovor 10 je netačan. Ograda ima 10 sekcija, ali 11 poruka.

Obrnuta greška se podiže kada je broj poruka poznat i broj sekcija se smatra itim. Stvarni broj sekcija je ѕa jedan manji od broja posta.

U generalnom, problem može da glasi:

Tačan odgovor može biti n − 1, ako je linija stubova otvoreno-završena, n ako formira petlju, ili n + 1 ako se otvorene strane sekvenci stubova smatraju sekcijama. Precizna definicija problema mora biti oprezno razmatrana, pošto podešavanje za jednu situaciju može dati pogrešan odgovor za druge situacije. Grečke ograđenih poruka dolaze iz brojanja stvari više nego iz prostora između njih, ili obrnuto, ili zanemarivanjem razmatranja da li bi trebalo da broji jedan ili oba kraja reda.

Greške ograđenih poruka se mogu prijaviti u jedinicama koje nisu dužine. Na primer, Vremenska Piramida, koja se sastoji od 120 blokova postavljnih u intervali od 10 godina između blokova, planirano je da traje 1190(ne 1200) godina da se napravi, od instalacije prvog bloka do poslednjg. Jedna od najranijih grešaka ograđenih poruka koja uključuje vreme, bila je Julijanski kalendar originalno je izračunavao skokove godina netačno, zbog zaključnog brojanja a ne isključnog, dajuči skok godine svake treće godine a ne četvrte.

"Greška ograđene poruke" može, u retkim situacijama, da se odnosi na grešku izazvane neočekivanim pravilnostima u ulaznim vrednostima, koji može (na primer) u potpunosti onemogućiti teorisku efikasnu implementaciju binarnog stabla ili heš funkciju. Ova greška uključuje razliku između očekivanih i ponašanja najgoreg slučaja algoritama.

Kod većih brojeva biti greška za jedan nije često veliki problem, Kod manjih brojeva, međutim, i specifičnim slučajevima kod kojih je preciznost najvažnija za izvršenje greške za jedan može biti katastrofalna. Ponekad takav problem će takođe biti ponavljan i , samim tim, pogoršan, tako što će neko predati netačni proračun ako ta osoba napravi istu vrstu greške ponovo (naravno, greška može takođe biti obrnuta).

Primer ove greške se može javiti u računskom jeziku MATLAB-u sa linspace()funkcijom, čiji su parametri (manje vrednosti, veće vrednosti, broj vrednosti) i ne (manje vrednosti, veće vrednosti, broj koraka ). Programer koji pomeša treći parametar da bude broj koraka može se ponadati da linspace(0,10,5) će postići sekvencu [0, 2, 4, 6, 8, 10] ali umesto toga dobiće [0, 2.5, 5, 7.5, 10].

Bezbedosne implikacije

Često greška za jedan rezultuje bubu bezbednosti koja je prouzrukovana zloupotrebom S standardne bibliotekestrncat rutine. Uobičajna zabluda sastrncat je da garantovana nula prekida se neće pisati iznad maksimalne dužine. U realnosti to će pisati lika nule prekida jedan bajt iznad maksimalne određene dužine. Sledeći kod sadrži takav bag:

void foo (char *s) 
{
    char buf[15];
    memset(buf, 0, sizeof(buf));
    strncat(buf, s, sizeof(buf)); // Коначни параметар би требало да буде: величине (buf)-1
}

Greška za jedan je česta u korišćenju S biblioteke zato što nije u skladu s obzirom na to da li jedan treba da uduzme 1 bajt- funkcije tipa fgets() i strncpy nikada neće pisati pored date dužine (fgets() oduzima 1 sama sebi, i vraća samo (dužinu -1) bajta), dok drugi, kao strncat će pisati pored date dužine. Dakle programer mora da zapamti kojim funkcijama trebaju da oduzimaju 1.

Na nekim sistemima (little endian arhitekture posebno) ovo može dovesti do prepisivanja najmanje značajnog bajta okvira pokazivača. Ovo može prouzrokovati stanje eksploatacije gde napadač kidnapuje lokalne promenljive za pozivanje rutine.

Jedan pristup koji često pomaže izbegavanje ovakvog problema je korišćenje varijanti ovih funkcija koji računaju koliko da pišu bazirajući se na totalnoj dužini bafera, pre nego na pisanje maksimalnog broja likova. Takve funkcije uključuju strlcat и strlcpy, i često se smatraju "sigurnijim" zato što ga čine lakšim za izbegavanje slučajnog pisanja pored kraja bafera.(U primeru koda iznad, pozivanjem strlcat(buf, s, sizeof(buf)) umesto će ukloniti bag.)

Vidi još

Literatura

An earlier version of this article was based on fencepost error at FOLDOC, used with permission.
Dijkstra, Edsger Wybe (2. 5. 2008). „Why numbering should start at zero (EWD 831)”. E. W. Dijkstra Archive. University of Texas at Austin. Pristupljeno 2011-03-16.