Грешка за један

Грешка за један (OBOE), је често познат као OBOB (баг за један), је логичка грешка која укључује дискретну једнакост услова граница. Често се активира у програмирању када се понавља управљање током када се понавља једном сувишно или премало. Овај проблем се може подићи када програмер направи грешку користећи " мање од или једнако" где "мање од " би требало да се користи у поређењу или грешкама да одведе до профила који секвенца стартује на нули више него једном (као што је са индексима реда у многим језицима). Ово се може појавити и у математичком контексту.

Петљање над редовима

Размотрити низ чланова, и чланове m кроз n (закључно) који ће бити процесовани. Колико је чланова тамо? Интуитивни одговор може бити n - m, али то је грешка за један, који показује грешку ограђена порука; тачан одговор је n –m + 1.

Из овог разлога, опсег у рачунарству је често представљен преко полуотворених интервала; опсег од m до n (закључно) је представљен опсегомод m (закључно до n + 1 (незакључно) како би се избегле грешке ограђене поруке. На пример, петља која се понавља 5 пута може бити записана као полуотворени интервал од 0 до 5:

for (i = 0; i < 5; i++) 
{
    /* Тело петље */
}

Тело петље је извршено преко i једнако са 0; i онда постаје 1, 2, 3, и на крају 4 при успешним понављањима. У том тренутку, i постаје5, тако да i < 5 је нетачно и петља се завршава. Међутим, ако је ово поређење коришћено <= (мање или једнако), петља би се извршила шест пута: i узима вредности 0, 1, 2, 3, 4, и 5. Исто тако, ако је i постављено на 1 а не на 0, било би само 4 понављања: i узима вредности 1, 2, 3, и 4. Обе ове алтернативе могу бити узрок грешке за један.

Још једна оваква грешка се може десити ако се do while петља користи уместо while петље(или обрнуто). Do wihle петља гарантује да ће радити само једном.

Повезана са редом конфузија може такође резултовати из разлика у програмским језицима. Бројање од 0 је најчешће, али неки језици почињу бројање од 1. Паскал има низове са индексима дефинисаним преко корисника. Ово омогућује да се моделују индекси низа после домена проблема.

Грешка ограђене поруке

Ограда са n секција има n+1 поста.

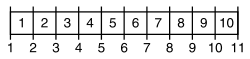
Грешка ограђене поруке (обично се назива стуб телеграфа или грешка поруке лампе ) је специјалан тип грешке за један. Следећи проблем илуструје грешку.

Интуитивни одговор 10 је нетачан. Ограда има 10 секција, али 11 порука.

Обрнута грешка се подиже када је број порука познат и број секција се сматра итим. Стварни број секција је ѕа један мањи од броја поста.

У генералном, проблем може да гласи:

Тачан одговор може бити n − 1, ако је линија стубова отворено-завршена, n ако формира петљу, или n + 1 ако се отворене стране секвенци стубова сматрају секцијама. Прецизна дефиниција проблема мора бити опрезно разматрана, пошто подешавање за једну ситуацију може дати погрешан одговор за друге ситуације. Гречке ограђених порука долазе из бројања ствари више него из простора између њих, или обрнуто, или занемаривањем разматрања да ли би требало да броји један или оба краја реда.

Грешке ограђених порука се могу пријавити у јединицама које нису дужине. На пример, Временска Пирамида, која се састоји од 120 блокова постављних у интервали од 10 година између блокова, планирано је да траје 1190(не 1200) година да се направи, од инсталације првог блока до последњг. Једна од најранијих грешака ограђених порука која укључује време, била је Јулијански календар оригинално је израчунавао скокове година нетачно, због закључног бројања а не искључног, дајучи скок године сваке треће године а не четврте.

"Грешка ограђене поруке" може, у ретким ситуацијама, да се односи на грешку изазване неочекиваним правилностима у улазним вредностима, који може (на пример) у потпуности онемогућити теориску ефикасну имплементацију бинарног стабла или хеш функцију. Ова грешка укључује разлику између очекиваних и понашања најгорег случаја алгоритама.

Код већих бројева бити грешка за један није често велики проблем, Код мањих бројева, међутим, и специфичним случајевима код којих је прецизност најважнија за извршење грешке за један може бити катастрофална. Понекад такав проблем ће такође бити понављан и , самим тим, погоршан, тако што ће неко предати нетачни прорачун ако та особа направи исту врсту грешке поново (наравно, грешка може такође бити обрнута).

Пример ове грешке се може јавити у рачунском језику MATLAB-у са linspace()функцијом, чији су параметри (мање вредности, веће вредности, број вредности) и не (мање вредности, веће вредности, број корака ). Програмер који помеша трећи параметар да буде број корака може се понадати да linspace(0,10,5) ће постићи секвенцу [0, 2, 4, 6, 8, 10] али уместо тога добиће [0, 2.5, 5, 7.5, 10].

Безбедосне импликације

Често грешка за један резултује бубу безбедности која је проузрукована злоупотребом С стандардне библиотекеstrncat рутине. Уобичајна заблуда саstrncat је да гарантована нула прекида се неће писати изнад максималне дужине. У реалности то ће писати лика нуле прекида један бајт изнад максималне одређене дужине. Следећи код садржи такав баг:

void foo (char *s) 
{
    char buf[15];
    memset(buf, 0, sizeof(buf));
    strncat(buf, s, sizeof(buf)); // Коначни параметар би требало да буде: величине (buf)-1
}

Грешка за један је честа у коришћењу С библиотеке зато што није у складу с обзиром на то да ли један треба да удузме 1 бајт- функције типа fgets() и strncpy никада неће писати поред дате дужине (fgets() одузима 1 сама себи, и враћа само (дужину -1) бајта), док други, као strncat ће писати поред дате дужине. Дакле програмер мора да запамти којим функцијама требају да одузимају 1.

На неким системима (little endian архитектуре посебно) ово може довести до преписивања најмање значајног бајта оквира показивача. Ово може проузроковати стање експлоатације где нападач киднапује локалне променљиве за позивање рутине.

Један приступ који често помаже избегавање оваквог проблема је коришћење варијанти ових функција који рачунају колико да пишу базирајући се на тоталној дужини бафера, пре него на писање максималног броја ликова. Такве функције укључују strlcat и strlcpy, и често се сматрају "сигурнијим" зато што га чине лакшим за избегавање случајног писања поред краја бафера.(У примеру кода изнад, позивањем strlcat(buf, s, sizeof(buf)) уместо ће уклонити баг.)

Види још

Литература

An earlier version of this article was based on fencepost error at FOLDOC, used with permission.
Dijkstra, Edsger Wybe (2. 5. 2008). „Why numbering should start at zero (EWD 831)”. E. W. Dijkstra Archive. University of Texas at Austin. Приступљено 2011-03-16.