Derivativi stabilnosti


Derivativi stabilnosti, su ujedno i derivativi upravljivosti, a predstavljaju meru (gradijent) pojedinih aerodinamičkih sila i momenata letelice po promeni njenih parametara leta (kao što su brzina, visina, napadni ugao, ugao klizanja, otklon komandnih površina itd). Za definisano ravnotežno stanje, promene i oscilovanje vrednosti ovih parametara, posle svakog poremećaja. Jednačine kretanja se koriste za analizu ovih promena i oscilacija, nakon poremećaja. Derivativi stabilnosti i upravljivosti se koriste za linearizaciju (pojednostavljenje) ovih jednačina kretanja, tako da se stabilnost i upravljivost letelica mogu jednostavnije analizirati.
Derivativi stabilnosti i upravljivosti definišu i uslovljavaju promene oblika kretanja oko ravnotežnog stanja letelice. Skup svih derivativa stabilnosti i upravljivosti (zajedno sa drugim karakteristikama letelice), povezano u jednačinama kretanja predstavlja matematički model letelice. Ovi matematički modeli se koriste u simulatorima leta za inženjersku analizu stabilnosti i upravljivosti letelice, a u realnom vremenu, služe za obuku i trenažu pilota.
U inženjerskoj praksi, derivativi stabilnosti i upravljivosti se dele u tri grupacije:
- derivativi položaja (statički, po napadnom uglu α i uglu klizanja β),
- prigušni derivativi (dinamički, po ugaonoj brzini, oko osa letelice q, r i p) i
- unakrsni derivativi („kuplovani“, uticaj klizanja na valjanje letelice i obrnuto).
Fizikalnost
[uredi | uredi izvor]
Analitička definicija stabilnosti i upravljivosti se zasniva na sistemu linearnih jednačina, koje predstavljaju ravnotežno stanje letelice. U jednačinama se prikazuju sile i momenti u obliku zbira proizvoda njihovih gradijenata po određenom parametru i priraštaja toga parametra. Ovi gradijenti u bezdimenzionom obliku predstavljaju derivative stabilnosti i upravljivosti. Pošto je avion simetričan, u odnosu na vertikalnu ravan, u kojoj se nalazi i uzdužna osa, sasvim se odvojeno analiziraju jednačine uzdužne stabilnosti od poprečno-smerne.
Stabilnost i upravljivost letelice su neodvojivi pojmovi, te i svi derivativi imaju uticaj na te obe oblasti povezane problematike. Mnogi, sa manjim uticajem se zanemaruju, a dominantniji se uključuju u razmatranje.[1][2][3]
U uzdužnom kretanju
[uredi | uredi izvor]Uzdužna stabilnost i upravljivost proizilazi iz uslova ravnoteže duž osa „X“ i „Z“ i oko „Y“, iz praktičnih razloga, razmatrano u koordinatnom sistemu leta (brzinskom). U tome pokretnom sistemu, poklapa se „X“ osa i pravac kretanja letelice. Matematički prikaz tih ravnotežnih stanja su linerne jednačine, koje sadrže derivative stabilnosti, kao gradijente po određenom parametru leta. Jednačine ravnoteže:
Posle bezdimenisanja svih delova jednačina i njihovih sređivanja, u njihovim sabircima se pojavljuju derivativi stabilnosti (u bezdimenzionom obliku).
- – prirast uzgona po napadnom uglu (gradijent uzgona)
- – prirast momenta propinjanja po napadnom uglu, mera statičke stabilnosti (svodi se na proizvod rezerve statičke stabilnosti i gradijenta uzgona)
- – prigušenje momenta propinjenja, u zavisnosti od brzine promene napadnog ugla, gde je i vreme obezdimenzionisano s faktorom
- – prigušenje momenta propinjenja, u zavisnosti od ugaone brzine propinjanja
- – efikasnost krmila visine
- – prigušenje momenta propinjenja, u zavisnosti od ugaone brzine otklona krmila horizontalnog repa[1][4][5][6]
U poprečno-smernom kretanju
[uredi | uredi izvor]Linerne jednačine ravnoteže, u poprečno-smernom kretanju su:
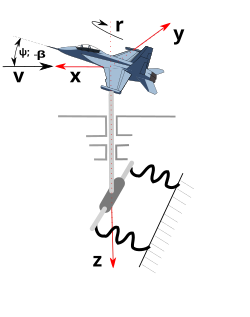
U njihovim sabircima se pojavljuju derivativi stabilnosti (u bezdimenzionom obliku).
- – prirast bočne sile, usled promene ugla klizanja
- – prigušni derivativ u valjanju, po ugaonoj brzini valjanja p
- – unakrsni (spregnuti) derivativ, moment valjanja usled ugaone brzine skretanja r
- – unakrsni derivativ, moment skretanja usled ugaone brzine valjanja p
- – prigušni derivativ, moment skretanja usled ugaone brzine skretanja r
- – efikasnost krilaca
- – efikasnost krmila pravca[1][7][8][9]
Metode određivanja vrednosti derivativa
[uredi | uredi izvor]Analitička
[uredi | uredi izvor]U početnoj fazi projektovanja, derivativi stabilnosti se određuju analitički. To je praktično prvo približavanje u projektovanju, kada se prema doprinosima pojedinih delova letelice određuju sabirci odeđenog derivativa. Ti doprinosi se određuju proračunski i na osnovu statistike poznatih vrednosti za dotični deo letelice.

U tom obliku se koriste za preliminarne faze projektovanja (prvom približavanju), u prvim simulacijama stabilnosti i upravljivosti letelice.[1]
Eksperimentalna, u aerotunelu
[uredi | uredi izvor]
U narednoj fazi projekta letelice, kada je poznat preliminarni njen oblik i geometrija, tada se izrađuje njen fizički model u smanjenoj razmeri, za ispitivanje aerodinamike u aerotunelu. U okviru tih ispitivanja je i merenje derivativa.
Merenje derivativa u aerotunelu se zasniva na dva principa:
- metod poremećaja s tipičnim kratkotrajnim ulazom, odgovor slobodne oscilacije i
- metod dugotrajne prinude, krutim oscilacijama
Kod oba medoda, snima se odgovor i na osnovu njegove analize, izdvajaju se odgovarajući derivativi. Za ova merenja je potrebno obezbediti odgovarajuće merne uređaje i mernu postavu. Neki od mernih uređaja su ilustrovani na priloženim slikama.
Posle ove eksperimentalne faze određuju se vrednosti derivativa, za nivo prototipskog razvoja letelice.[10][11][12]
Eksperimentalna, u letu i razvojnom simulatoru
[uredi | uredi izvor]Sledeća faza je merenje u letu, pri ispitivanju prorotipa. Sa ugrađenom specijalnom opremom i rasporedom senzora (davača), snima se odgovor aviona u letu na uvedeni tipični poremećaj. Matematičkom analizom toga odgovora vrši se identifikacija aeredinamičkih parametara aviona, među kojima i derivativa.
Metode identifikacije aerodinamičkih parametara u letu zasnivaju se na dobro poznatim teorijskim postavkama. Dobijeni rezultati međusobno se usaglašavaju na nivou projekta i koriste se za ažuriranje baze aerodinamičkih podataka za dotičnu letelicu, u svim konfiguracijama. Sistem dostiže zahtevani standard putem kompleksnog matematičkog modeliranja dinamike. Matematički model obuhvata veliki broj spoljnih i unutrašnjih parametara kao što su statički i dinamički pritisak i temperatura vazduha i njihov uticaj na ostale karakteristike. Zatim, obuhvata sve konfiguracije tereta i sve oblike i brzine leta letelice. Kvalitetan simulacioni model na prototipu omogućava prihvatljiv početni softver komandi leta bez ispitivanja u letu. Dobijeni rezultat se potvrđuje pouzdanošću prvih letova prototipova. Taj standard je osnova za dalji proces optimizacije sistema do konačnog rešenja. Konačno rešenje se postiže metodom upoređivanja i stalnog približavanja izmerenog odgovora realne letelice u letu i odgovora korigovanog modela na simulatoru (vidi princip na šemi ispod). Taj princip dobijanja kvalitetnog rešenja sistema može se nazvati hibridna simulacija, optimizacija metodom postepenog približavanja.
Osnova principa je snimanje odziva realne letelice i modela na simulatoru leta, na izabrani tipični ulaz, zatim njihovo poređenje, uočavanje međusobne razlike i preduzimanje korekcija nelinearnog modela i zakona upravljanja u smeru smanjenja tih razlika. Snimljeni odziv, preko matematičkih metoda analize, služi i za identifikaciju stvarnih sabiraka (gradijenata, odnosno derivativa) odgovarajuće aerodinamičke veličine kao što je dato u jednačini za otpor. Tim putem su aerodinamički podaci koriguju u bazi podataka i u relevantnim proračunima. Uklanjanje razlike u odzivu realizuje se sa popravkom nedostatatka nelinearnog matematičkog modela kroz korekciju njegovih elemenata sa novodobijenim podacima iz snimka odziva realnog aviona u letu. Korekcije se prioritetno sprovode na mestima većih razlika „odziva“ realne letelice i modela na simulatoru. Na taj način se postupno ažurira baza podataka nelinearnog modela i saglasno tome se ponovo usklađuju zakoni upravljanja.
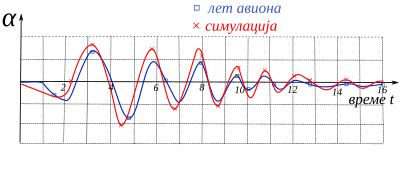
Metodom uzastopnog približavanja dolazi se do zadovoljavajućeg rešenja, uspostavlja se standard letelice prema važećim propisima, nameni i zahtevima pilota.
Aerodinamički otpor, može se razložiti na članove:[1]
Kao što je prilaz za kretanje duž x ose, isto važi i za sve stepene slobode kretanja letelice, duž sve tri ose i za rotaciju oko njih.
U prethodnoj jednačini je data zavisnost koeficijenta otpora letelice sa doprinosom njegovog rasta usled promene napadnog ugla, otklona komandne površne i prigušenja zbog ugaone brzine rotacije.
Gradijenti aerodinamičkih veličina po promenljivoj su aerodinamički derivativi. Po istom principu je identifikovan i moment propinjanja, pa i ostale karakteristike:[1]
Ovom metodom se uspešno ažurirana baza podataka nelinernog modela. Korišćeni algoritam greške u odzivu realne letelice i modeliranog nelinearnog paketa svodi razliku na minimum. Time je napravljena realna osnova za izbor optimalnih zakona upravljanja letelicom, to jest, obezbeđena je „pamet“ komandnom sistemu za efikasno upravljanje s njom u celoj anvelopi leta i u svim konfiguracijama.[13]
Upotreba
[uredi | uredi izvor]Linearizacija jednačina kretanja i simulacija
[uredi | uredi izvor]Uvođenjem pojmova derivativa (uprošćavanjem samo s prvostepenim diferenciranjem) izvršena je linearizacija jednačina kretanja letelice. Simulacija leta se zasniva na toj linearizaciji jednačina kretanja letelica, što se zasniva na pretpostavci malih poremećaja. Ta aproksimacija zadovoljava potrebe projekta. U cilju aerodinačkog projektovanja stabilnosti i upravljivosti letelice (uključujući i komande leta), simulacijom se kreće od samog početka projekta, sa početnim podacima za derivative, masu i momente inercije itd.
Simulacija leta letelice omugućuje projekat razvojnog simulatora, čiji je doprinos opisan u prethodnom poglavlju i učila za obuku pilota na zemlji (simulatora leta).[1][13]
Simulatori leta za obuku pilota
[uredi | uredi izvor]
Simulator leta je uređaj koji simulira uslove i karakteristike leta vazduhoplova i sredine u kojoj se isti realizuje. Na njemu se vrši obuka, provera i trenaža pilota, na zemlji, sa čime se uštede velika finansijska sredstva. Uključujući repliciranje jednačina, koje matematički predstavljaju fizikalnost leta letelice, reakciju na primenu upravljačkih komandi, efekte svih sistema vazduhoplova i reakciju na spoljne faktore, kao što su gustina vazduha, turbulencija, udari vetra, padavine itd. (spoljne poremećaje). Simulatori leta se koriste u toku školovanja i održavanje trenaže pilota. U inženjerstvu se koristi u toku razvoja aviona, posebno projekta stabilnosti, upravljivosti i sistma komandi leta, što je onavedeno u prethodnom poglavlju.[14]
Simulatori leta sadrže različite vrste hardvera i softvera, u zavisnosti od modeliranja detalja i simulacije radnji. Projekti sadrže varijante u rasponu od simulacije na laptopu, na bazi modela sistema vazduhoplova, do potpune replike kabine letelice za početno upoznavanje, pa do potpuno realnih simulacija kabine, komandi leta i ostalih sistema vazduhoplova, za višu i kompletnu obuku pilota. Najviši nivo simulatora leta su za obuku pilota putničkih aviona, a za obuku vojnih pilota je nešto niži. Na primer, međunarodni viši nivo zahteva kretanja platforme sa kabinom simulatora, u okviru svih šest stepeni slobode i vizuelni sistemom, u okviru vidljivosti od 150 h 40, za celu populaciju pilota. Vojni simulatori leta imaju više varijacija u projektovanju.[15][16]
Vidi još
[uredi | uredi izvor]Reference
[uredi | uredi izvor]- ^ a b v g d đ e Nenadović, Miroslav (1971). „Aerodinamički derivativi”. Stabilnost i upravljivost letelica (na jeziku: (jezik: srpski)). Beograd. 741: 668—712.
- ^ Rendulić, Zlatko (1987). „Uvod u stabilnost i upravljivost”. Mehanika leta (na jeziku: (jezik: srpski)). Beograd. 615: 273—279.
- ^ Perkins, C.D., Hage, r.E. Aeroplane Performance Stability and Control, John Wiley, New York, 1950.
- ^ Rendulić, Zlatko (1987). „Derivativi i parametri u jednačinama kretanja”. Mehanika leta (na jeziku: (jezik: srpski)). Beograd. 615: 457—459.
- ^ „Longitudinal stability derivatives” (PDF) (na jeziku: (jezik: engleski)). aerostudents.com. Arhivirano iz originala (pdf) 23. 08. 2013. g. Pristupljeno 19. 8. 2013. „Longitudinal stability derivatives”
- ^ Perkins, C.D., Hage, r.E. Aeroplane Performance Stability and Control, John Wiley, New York, p 65, 1950.
- ^ Rendulić, Zlatko (1987). „Sumiranje derivativa i koeficijenata momenata valjanja i skretanja”. Mehanika leta (na jeziku: (jezik: srpski)). Beograd. 615: 433—4436.
- ^ „Lateral stability derivatives” (PDF) (na jeziku: (jezik: engleski)). aerostudents.com. Arhivirano iz originala (pdf) 23. 08. 2013. g. Pristupljeno 19. 8. 2013. „Lateral stability derivatives”
- ^ Perkins, C.D., Hage, r.E. Aeroplane Performance Stability and Control, John Wiley, New York, p 83, 1950.
- ^ Mesure des derivees aerodynamiquesen eceouulement transonique et supersonique, Sherer, Publication N0 104, 1962.g.
- ^ S. Pustinja, Studija derivativa poprečno-smerne stabilnosti , Saopštenje VTI-a, 1968.
- ^ S. Pustinja, Merenje efikasnosti krilaca aviona u aerotunelu , Vojnotehnički glasnik, 1970.
- ^ a b v Renzo Bava; Graham T. Hoare; Gabriel Garcia-Mesuro; Hans-Christoph Oelker. „Recent Experiences on Aerodynamic Parameter Identification for EUROFIGHTER at Alenia, British Aerospace, CASA and Daimler-Benz Aerospace” (PDF) (na jeziku: (jezik: engleski)). Arhivirano iz originala (PDF) 03. 03. 2012. g. Pristupljeno 18. 8. 2013. „Identifikacija aerodinačkih parametara tajfuna”
- ^ „Pilotažnый trenažer samoleta SSJ 100 gotov k obučeniю rossiйskih pilotov” (na jeziku: (jezik: ruski)). ato.ru. 22. 11. 2011. Pristupljeno 11. 8. 2013. „Pilotažnый trenažer samoleta SSJ 100 gotov k obučeniю rossiйskih pilotov”
- ^ „ASME International The Link Flight Trainer” (PDF) (na jeziku: (jezik: engleski)). files.asme.org. Arhivirano iz originala (pdf) 17. 12. 2011. g. Pristupljeno 19. 8. 2013. „ASME International The Link Flight Trainer”
- ^ „U.S. Air Force Fact Sheet LINK TRAINER” (na jeziku: (jezik: engleski)). nationalmuseum.af.mil. Arhivirano iz originala 24. 01. 2012. g. Pristupljeno 19. 8. 2013. „LINK TRAINER”



















