Момент инерције

Момент инерције
Замајаци имају велике моменте инерције да би изравнали ротационо кретање.
Уобичајени симболи	I
СИ јединица	kg m²
Друге јединице	lbf·ft·s2
СИ димензија	M L2
Деривације из других квантитета	$I={\frac {L}{\omega }}$

Шетачи уским ужетима користе моменат инерције дугог штапа за равнотежу док ходају ужетом. Самуел Дикон прелазећи реку Ниагару 1890.

Момент инерције је мера инертности тела при ротационом кретању. Момент инерције је аналоган маси код транслаторног кретања. Појаву инерције први је проучавао Галилео Галилеј. Инерцију описује I Њутнов закон, по коме свако тело задржава стање мировања или равномерног праволинијског кретања док га неко друго тело не присили да то стање промени. Инертност је својство тела да се одупире промени стања мировања или равномерног праволинијског кретања. Тела веће масе су инертнија (тромија). Маса је мера интерности тела.

Клизачица код окретања смањује свој момент тромости или момент инерције скупљајући руке уз тело како би се брже окретала.

Трактор с вањским замајцом (с великим моментом тромости) који служи да уједначује окретање мотора (без трзаја).

Код ходања по ужету користи се момент инерције дугог штапа како би се повећала равнотежа.

Момент инерције (знак I или J) је једнак збиру умножака масе m и квадрата удаљености r од осе ротације сваке честице која чини тело:

$I=\sum _{i=1}^{N}m_{i}{r_{i}}^{2}$

Момент инерције је заправо мера тромости за вртњу или ротацијско кретање. Може се рећи да је момент инерције ротацијска аналогија масе. Што је момент инерције неког тела већи то га је теже покренути у ротацију или зауставити његову ротацију. Међутим, за разлику од масе, момент инерције није нека непромењива величина; он зависи од осе око које се дешава ротација тела. Математичка дефиниција момента инерције I материјалне тачке масе m за неку осу a је:

$I_{a}=mr^{2}\,$

где је r удаљеност те тачке од осе ротације. Мерна јединица за момент инерције је kgm².

За неко тело састављено од N материјалних честица момент инерције за неку осу је једнак збиру момената инерције свих материјалних честица за ту исту осу:

$I_{a}=\sum _{i=1}^{N}m_{i}{r_{i}}^{2}$

Ово је непрактичан израз за неко континуирано тело за који би требало знати тачан број и положај свих честица. Уместо тога интегрирају се моменти инерције свих диференцијалних маса dm:

$I_{a}=\int r^{2}dm=\int r^{2}\rho dV$

Уз претпоставку да је густина тела ρ по целој запремини једнака, добија се:

$I_{a}=\rho \int r^{2}dV=\rho \iiint r^{2}dxdydz$

Моменти инерције за оси које пролазе кроз тежиште тела називају се властитим моментима инерције. Иако горња математичка формулација вреди потпуно генерално, момент инерције за неку осу која пролази изван тежишта тела се може израчунати помоћу Стајнеровог правила које се може овако срочити:

Момент инерције тела за неку осу која не пролази кроз тежиште једнак је збиру властитог момента инерције за осу паралелну с траженом осом и умношка масе тела с квадратом удаљености тежишта тела од тражене осе .

Ово је правило врло важно и елементарно. Умножак масе тела и квадрата удаљености тежишта тела од тражене осе се назива положајни момент инерције.

Математички изричај Штајнеровог правила може се записати на следећи начин:

$I=I_{vl}+mr^{2}=I_{vl}+J_{pol}\,$

Из свега изложенога треба уочити неколико чињеница битних за разумевање материје:

• Што је нека маса удаљенија од осе ротације, то је теже вршити ротацију.
• Инертност или тромост масе при ротацији расте с квадратом удаљености од осе ротације.
• Материјална тачка нема властитих момената инерције јер нема протежност.
• За довољно компактна тела (на пример мала кугла) у неким случајевима може се апроксимирати да немају властитих момената инерције.
• Момент инерције неког тела не зависи само о његовој маси и удаљености његовог тежишта од осе ротације, већ и од облика.
• Штајнерово правило се примењује без обзира на то да ли оса ротације пролази кроз тело или се налази изван њега, битан је само однос осе према тежишту.

Момент тромости неких тела

Момент тромости неког тела зависи од облика тела, расподеле масе, положаја осе ротације. На пример, ако је m маса тела, r његов полупречник, а оса ротације уједно и оса симетрије, момент инерције на пример шупљег ваљка или прстена износи:

$I=mr^{2}$

хомогено испуњеног ваљка или кружне плоче:

$I={\frac {mr^{2}}{2}}\,\!$

хомогено испуњене кугле:

$I={\frac {2mr^{2}}{5}}\,\!$

Момент тромости хомогено испуњеног штапа којем је оса ротације нормална на дужину штапа налази се на половини дужине штапа l:

$I={\frac {ml^{2}}{12}}\,\!$

а на крају је штапа:

$I={\frac {ml^{2}}{3}}\,\!$

где је: l - дужина штапа. Мерна је јединица момента тромости килограм пута квадратни метар (kg m²).

Моменти тромости неких пресека

Опис	Слика	Момент тромости	Примедба	Литература
пуни кружни пресек (шипка) с полупречником r		$I_{x}={\frac {\pi }{4}}r^{4}$ $I_{y}={\frac {\pi }{4}}r^{4}$ $I_{z}={\frac {\pi }{2}}r^{4}$
прстен (цев) с унутрашњим полупречником r1 и спољашњим полупречником r2		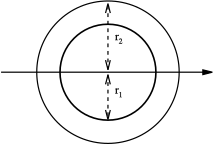$I_{x}={\frac {\pi }{4}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)$ $I_{y}={\frac {\pi }{4}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)$ $I_{z}={\frac {\pi }{2}}\left({r_{2}}^{4}-{r_{1}}^{4}\right)$	За танке цеви, $r\equiv r_{1}\approx r_{2}$ i $r_{2}\equiv r_{1}+t$. Може се рећи да $\left(r_{2}^{4}-r_{1}^{4}\right)=\left(\left(r_{1}+t\right)^{4}-r_{1}^{4}\right)=\left(4r_{1}^{3}t+6r_{1}^{2}t^{2}+4r_{1}t^{3}+t^{4}\right)$, и због $r_{1}>>t$ та заграда се може поједноставити у $\left(4r_{1}^{3}t+6r_{1}^{2}t^{2}+4r_{1}t^{3}+t^{4}\right)\approx 4r_{1}^{3}t$. Коначно, за танкозидну цев произлази, $I_{x}=I_{y}=\pi {r}^{3}{t}$.
пуни кружни исечак с углом θ у радијанима и полупречником r, с обзиром на осу која пролази кроз тежиште и средиште кружнице		$I_{0}=\left(\theta -\sin \theta \right){\frac {r^{4}}{8}}$	Једнакост вреди само за 0 ≤ $\theta$ ≤ $\pi$
пуни полукруг с полупречником r у односу на водоравни правац који пролази кроз тежиште		$I_{0}=\left({\frac {\pi }{8}}-{\frac {8}{9\pi }}\right)r^{4}\approx 0,1098r^{4}$
пуни полукруг с полупречником r у односу на водоравни правац који пролази кроз основу		$I={\frac {\pi r^{4}}{8}}$	Удаљеност између тежишта и основе је ${\frac {4r}{3\pi }}$
пуни полукруг с полупречником r у односу на нормални правац који пролази кроз тежиште		$I_{0}={\frac {\pi r^{4}}{8}}$
пуна четвртина круга с полупречником r с обзиром на средиште круга.		$I={\frac {\pi r^{4}}{16}}$
пуна четвртина круга с полупречником r s obzirom na pravac prolazi kroz težište		$I_{0}=\left({\frac {\pi }{16}}-{\frac {4}{9\pi }}\right)r^{4}\approx 0.0549r^{4}$	Удаљеност између тежишта и базе је ${\frac {4r}{3\pi }}$
пуна елипса с полуосама a (уздуж осе x) и b		$I_{x}={\frac {\pi }{4}}ab^{3}$ $I_{y}={\frac {\pi }{4}}a^{3}b$
пуни правоугаоник с основицом a и висином h у односу на правац који пролази кроз тежиште		$I_{x}={\frac {bh^{3}}{12}}$ $I_{y}={\frac {b^{3}h}{12}}$
пуни правоугао с основицом a и висином h у односу на правац који пролази кроз основицу		$I={\frac {bh^{3}}{3}}$
пуни троугао с основицом b и висином h у односу на правац који пролази кроз тежиште		$I_{0}={\frac {bh^{3}}{36}}$
пуни троугао с основицом b и висином h у односу на правац који пролази кроз основицу		$I={\frac {bh^{3}}{12}}$
пуни шестоугао са страницом a, правац пролази кроз тежиште или средиште		$I_{0}={\frac {5{\sqrt {3}}}{16}}a^{4}$	Исто вреди и за нормални правац.

Материјална тачка

За материјалну тачку се момент инерције изражава формулом I=mr². Момент инерције тела у општем случају рачуна се сумирањем момената инерције свих његових саставних делова. Код неких геометријских фигура се на тај начин добијају математички једноставније формуле, док код сложенијих тела сагласно томе повећава и комплексност рачуна који се изискује за њихово одређивање и примену. У општем случају можемо тај поступак описати овако:

$I=\sum _{i=1}^{N}{m_{i}r_{i}^{2}}\,\!$

За лопту он се рачуна обрасцем ${\textstyle {\frac {2mr^{2}}{5}}}$, за ваљак (хомогени диск) ${\textstyle {\frac {mr^{2}}{2}}}$, а за хомогени штап ${\textstyle {\frac {2ml^{2}}{12}}}$, где је $r$ полупречник (код лопте и ваљка), а $l$ дужина штапа. За израчунавање момента инерције често се користи Штајнерова теорема. У питању је скаларна величина, а често се користи у тензорском облику.

Примена

Савијање

Главни чланак: Савијање

Греда је издужена водоравна или коса носива грађевна конструкција за преношење вертикалних оптерећења на лежаје, ослоњена на својим крајевима (на једној страни помично, на другој непомично). Према броју лежаја разликују се греда с једним лежајем (конзолна), с два лежаја (просто ослоњена, с препустима), с више лежаја (континуирана).

Замашњак на парној локомотиви из 1802.

Изглед једног инерцијског навигацијског система (жироскоп) на француском балистичком пројектилу IRBM S3.

Савијање или флексија (енгл. bending, flexure) је оптерећење које делује нормално на уздужну осу носача. За разлику од осног оптерећења (истезање и притисак), при савијању штапа деформише се уздужна оса штапа. Деформирана уздужна оса зове се еластична линија или прогиб. Разликује се чисто савијање и попречно савијање. При чистом савијању све су компоненте унутрашњих сила једнаке нули, осим момента савијања. При попречном савијању осим момента савијања појављује се још и попречна сила која узрокује смицање. Чисто савијање зове се још и савијање спреговима, а попречно савијање, савијање силама. Момент савијања узрокује нормална напрезања σ која се замишљају раздељенима по пресеку сразмерно удаљености од неутралне осе. Неутрална оса пролази кроз тежиште проматраног пресека. Класична једнакост која одређује напрезање у греди услед деловања чистог савијања је:

${\sigma }={\frac {M\cdot y}{I_{x}}}$

где је: ${\sigma }$ - напрезање услед савијања, M - момент савијања око неутралне осе x, y - нормална удаљеност од неутралне осе x, I_x - момент тромости или момент инерције око неутралне осе x.

Максимално напрезање на савијање σ<суб>маx</суб> појављује се у тачки која је најудаљенија од неутралне осе y_max:

$\sigma _{max}={\frac {M\cdot y_{max}}{I_{x}}}={\frac {M}{W_{x}}}$

где је: ${W_{x}}$ - момент отпора пресека.

Прогиб носача ${\delta }$ произлази из диференцијалне једнакости еластичне линије:

${\delta }={\frac {M_{x}}{E\cdot I_{x}}}$

Уобичајене вредности за максималне моменте савијања, прогибе, моменте тромости и моменте отпора пресека могу се наћи у таблицама.

Литература

• Goldstein, H. (1980). Classical Mechanics (2nd изд.). Addison-Wesley. ISBN 0-201-02918-9. .
• Landau, LD; Lifshitz, EM (1976). Mechanics (3rd изд.). Pergamon Press. ISBN 0-08-021022-8. ; ISBN 0-08-029141-4 (softcover).}}
• Marion, JB; Thornton, ST. (1995). Classical Dynamics of Systems and Particles (4th изд.). Thomson. ISBN 0-03-097302-3. .
• Sylvester, J J (1852), „A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of a sum of positive and negative squares” (PDF), Philosophical Magazine, IV: 138—142, Приступљено 27. 6. 2008 CS1 одржавање: Формат датума (веза)
• Symon, KR (1971). Mechanics (3rd изд.). Addison-Wesley. ISBN 0-201-07392-7. .
• Tenenbaum, RA (2004). Fundamentals of Applied Dynamics. Springer. ISBN 0-387-00887-X. .

Спољашње везе

• Angular momentum and rigid-body rotation in two and three dimensions Архивирано на сајту Wayback Machine (29. март 2010)
• Lecture notes on rigid-body rotation and moments of inertia
• The moment of inertia tensor
• An introductory lesson on moment of inertia: keeping a vertical pole not falling down (Java simulation)
• Tutorial on finding moments of inertia, with problems and solutions on various basic shapes Архивирано на сајту Wayback Machine (14. август 2009)
• Notes on mechanics of manipulation: the angular inertia tensor