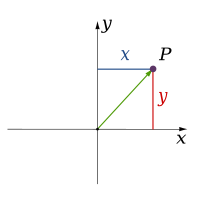Dimenzija

Primer dvodimenzionalnog (kvadrat), trodimenzionalnog (kocka) i četvorodimenzionalnog objekta (hiperkocka), sleva nadesno. Višedimenzionalni objekat u nižoj dimenziji može se prikazati jedino projekcijom.

Dimenzija u matematici ili fizici predstavlja minimalni broj koordinata potrebnih da se opiše bilo koja tačka na zadatom telu ili u zadatom prostoru.

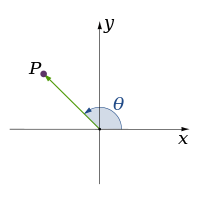
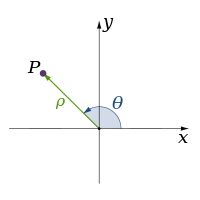
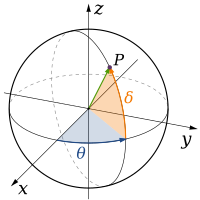
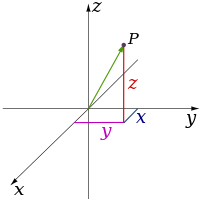
• U klasičnoj mehanici koriste se tri prostorne dimenzije: dužina, širina i visina koje čine Dekartov koordinatni sistem (x, y, z) i zadaju prostor. Pored Dekartovog koordinatnog sistema, koriste se i drugi koordinatni sistemi za opis trodimenzionalnog prostora, među kojima se najčešće koriste cilindrični koordinantni sistem (r, φ, z) i sferni koordinatni sistem (r, φ, θ).
• U matematici (algebri) koriste se višedimenzionalni vektorski prostori.

• U fizici, u teoriji relativnosti, za opis sistema se koristi četvorodimnezionalni prostor koji pored tri prostorne koordinate (x, y, z) imaju i četvrtu koordinatu - vreme. Najčešće se koristi prostor Minkovskog (x, y, z, t).
• U elektromagnetizmu se dinamika sistema može zapisati koristeći standardan trodimenzionalni prostor, ali se jednačine koje opisuju sistem (Maksvelove jednačine) značajno pojednostavljuju ako se koristi četvorodimenzionalni prostor sa vremenom kao četvrtom koordinatom, (x, y, z, t).
• U teoriji struna, koristi se desetodimenzionalni prostor.

Fizika

Prostorne dimenzije

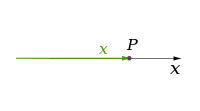
Teorije klasične fizike opisuju tri fizičke dimenzije: sa određene tačke u prostoru, osnovni pravci u kojima se može kretati su gore/dole, levo/desno i napred/nazad. Kretanje u bilo kom drugom pravcu može se izraziti u smislu ova tri. Kretanje nadole je isto što i kretanje gore na negativnoj udaljenosti. Kretanje dijagonalno nagore i napred je baš kao što naziv smera implicira; odnosno kretanje u linearnoj kombinaciji gore i napred. U svom najjednostavnijem obliku: linija opisuje jednu dimenziju, ravan opisuje dve dimenzije, a kocka opisuje tri dimenzije. (Pogledajte prostor i kartezijanski koordinatni sistem.)

Broj dimenzija	Primeri koordinatnih sistema
1	Brojevna prava Ugao
2	Katezijanski (two-dimensional) Polarni Latituda i longituda
3	Katezijanski (trodimenzioni) Cilindrični Sferični

Vreme

Temporalna dimenzija, ili vremenska dimenzija, je dimenzija vremena. Vreme se iz tog razloga često naziva „četvrtom dimenzijom“, ali to ne znači da je to prostorna dimenzija. Vremenska dimenzija je jedan od načina da se izmeri fizička promena. Ona se percipira drugačije od tri prostorne dimenzije po tome što postoji samo jedna, kao i po tome da se ne može slobodno kretati u vremenu već subjektivno u jednom pravcu.

Jednačine koje se koriste u fizici za modelovanje stvarnosti ne tretiraju vreme na isti način na koji ga ljudi obično percipiraju. Jednačine klasične mehanike su simetrične u odnosu na vreme, a jednačine kvantne mehanike su tipično simetrične ako su vreme i druge veličine (kao što su naelektrisanje i paritet) obrnute. U ovim modelima, percepcija vremena koje teče u jednom pravcu je artefakt zakona termodinamike (mi percipiramo vreme kao da teče u pravcu povećanja entropije).

Najpoznatiji tretman vremena kao dimenzije je Poenkareova i Ajnštajnova specijalna relativnost (i proširena na opštu relativnost), koja tretira percipirani prostor i vreme kao komponente četvorodimenzionalne mnogostrukosti, poznate kao prostor-vreme, a u posebnom, ravnom slučaju kao prostor Minkovskog. Vreme se razlikuje od drugih prostornih dimenzija jer vreme deluje u svim prostornim dimenzijama. Vreme deluje u prvoj, drugoj i trećoj, kao i teorijskim prostornim dimenzijama kao što je četvrta prostorna dimenzija. Vreme, međutim, nije prisutno u jednoj tački apsolutne beskonačne singularnosti koja je definisana kao geometrijska tačka, jer beskonačno mala tačka ne može imati nikakvu promenu, a samim tim ni vreme. Baš kao što se objekat kreće kroz pozicije u prostoru, on se takođe kreće kroz pozicije u vremenu. U tom smislu sila koja pokreće bilo koji objekat da se promeni je vreme.

Dodatne dimenzije

U fizici su tri dimenzije prostora i jedna dimenzija vremena prihvaćena norma. Međutim, postoje teorije koje pokušavaju da ujedine četiri fundamentalne sile uvođenjem dodatnih dimenzija/hiperprostora. Najvažnije, teorija superstruna zahteva 10 prostorno-vremenskih dimenzija i potiče od fundamentalnije 11-dimenzionalne teorije koja se uslovno naziva M-teorija koja obuhvata pet prethodno različitih teorija superstruna. Teorija supergravitacije takođe promoviše 11D prostor-vreme = 7D hiperprostor + 4 zajedničke dimenzije. Do danas, nema direktnih eksperimentalnih ili opservacijskih dokaza koji bi podržali postojanje ovih dodatnih dimenzija. Ako hiperprostor postoji, on mora biti skriven od nas nekim fizičkim mehanizmom. Jedna dobro proučena mogućnost je da se dodatne dimenzije mogu „smotati” u tako malim razmerama da budu efektivno nevidljive za trenutne eksperimente. Ograničenja veličine i drugih svojstava dodatnih dimenzija su postavljena eksperimentima na česticama kao što su oni na Velikom hadronskom sudaraču.

Godine 1921, teorija Kaluza–Klajna je predstavila 5D uključujući dodatnu dimenziju prostora. Na nivou kvantne teorije polja, teorija Kaluza–Klajna objedinjuje gravitaciju sa meračkim interakcijama, na osnovu spoznaje da je gravitacija koja se širi u malim, kompaktnim dodatnim dimenzijama ekvivalentan merač interakcijama na velikim udaljenostima. Naročito kada je geometrija dodatnih dimenzija trivijalna, ona reprodukuje elektromagnetizam. Međutim, na dovoljno visokim energijama ili kratkim udaljenostima, ova postavka i dalje pati od istih patologija koje su dobro poznate da ometaju direktne pokušaje da se opiše kvantna gravitacija. Stoga, ovi modeli i dalje zahtevaju UV završetak, onakvog oblika kakav teorija struna treba da obezbedi. Konkretno, teorija superstruna zahteva šest kompaktnih dimenzija (6D hiperprostor) koje formiraju Kalabi-Jau mnogostrukost. Tako se teorija Kaluza-Klajna može smatrati ili kao nepotpun opis sam po sebi, ili kao podskup izgradnje modela teorije struna.

Pored malih i uvijenih dodatnih dimenzija, možda postoje dodatne dimenzije koje umesto toga nisu očigledne jer je materija povezana sa našim vidljivim univerzumom lokalizovana na (3 + 1)-dimenzionalnom podprostoru. Stoga dodatne dimenzije ne moraju biti male i kompaktne, već mogu biti velike dodatne dimenzije. D-brane su dinamički prošireni objekti različitih dimenzionalnosti predviđeni teorijom struna koji bi mogli igrati ovu ulogu. Oni imaju osobinu da su pobuđivanja otvorenih struna, koja su povezana sa interakcijama merača, ograničena na branu svojim krajnjim tačkama, dok su zatvorene žice koje posreduju u gravitacionoj interakciji slobodne da se šire u ceo prostor-vreme, ili „veliki deo“. Ovo bi moglo biti povezano sa razlogom zašto je gravitacija eksponencijalno slabija od drugih sila, jer se efikasno razblažuje dok se širi u zapreminu veće dimenzije.

Neki aspekti fizike brane su primenjeni na kosmologiju. Na primer, kosmologija branskog gasa pokušava da objasni zašto postoje tri dimenzije prostora koristeći topološka i termodinamička razmatranja. Prema ovoj ideji to bi bilo pošto je tri najveći broj prostornih dimenzija u kojima se nizovi generički mogu ukrštati. Ako u početku postoji mnogo namotaja žica oko kompaktnih dimenzija, prostor bi se mogao proširiti do makroskopskih veličina tek kada se ovi namotaji eliminišu, što zahteva suprotno namotane žice da se pronađu i unište. Ali žice mogu samo da pronađu jedna drugu da bi se poništile značajnom brzinom u tri dimenzije, tako da sledi da je samo u tri dimenzije prostorA dozvoljeno narastanje s obzirom na ovu vrstu početne konfiguracije.

Za dodatne dimenzije se kaže da su univerzalne ako su sva polja podjednako slobodna da se šire unutar njih.

Vidi još

• Geometrija
• Dekartov koordinatni sistem

Literatura

• Ayres, Frank (1965). Schaum's Outline of Modern Abstract Algebra (1st izd.). McGraw-Hill. ISBN 9780070026551. 
• Murty, Katta G. (2014). „1. Systems of Simultaneous Linear Equations” (PDF). Computational and Algorithmic Linear Algebra and n-Dimensional Geometry. World Scientific Publishing. ISBN 978-981-4366-62-5. doi:10.1142/8261. 
• Abbott, Edwin A. (1884). Flatland: A Romance of Many Dimensions. London: Seely & Co. 
  • —. Flatland: ... Project Gutenberg. 
  • —; Stewart, Ian (2008). The Annotated Flatland: A Romance of Many Dimensions. Basic Books. ISBN 978-0-7867-2183-2. 
• Banchoff, Thomas F. (1996). Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions. Scientific American Library. ISBN 978-0-7167-6015-3. 
• Pickover, Clifford A. (2001). Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons. Oxford University Press. ISBN 978-0-19-992381-6. 
• Rucker, Rudy (2014) [1984]. The Fourth Dimension: Toward a Geometry of Higher Reality. Courier Corporation. ISBN 978-0-486-77978-2.  Google preview
• Kaku, Michio (1994). Hyperspace, a Scientific Odyssey Through the 10th Dimension. Oxford University Press. ISBN 978-0-19-286189-4. 
• Krauss, Lawrence M. (2005). Hiding in the Mirror. Viking Press. ISBN 978-0-670-03395-9. 
• William Fulton. (1998), Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., 2 (2nd izd.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-62046-4, MR 1644323 

Spoljašnje veze

• Copeland, Ed (2009). „Extra Dimensions”. Sixty Symbols. Brady Haran for the University of Nottingham.